Expression for Back E.M.F. or Induced E.M.F. per phase in Synchronous Motor (Ebph)

Expression for Back E.M.F. or Induced E.M.F. per phase in Synchronous Motor (E_bph)

case i] Under excitation, E_bph < V_ph.

Z_S = R_a + j X_S = | Z_S| ∠ ϕ Ω

θ = tan^-1 (X_S / R_a )

E_Rph^ I_aph = θ I_a lags E_R always by angle θ

V_ph = Phase voltage applied

E_bph = Back e.m.f. induced per phase

E_Rph = I_a × Z_s V     ... Per phase 

Let p.f. be cos ϕ , lagging as under excited,

V_ph ^ I_aph = ϕ

Phasor diagram is shown in the Fig. 4.12.1. Applying cosine rule to ∆ OAB,

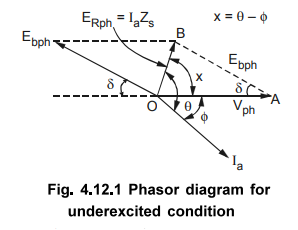
So once Ebpb is calculated, load angle 8 can be determined by using sine rule.

Case ii] Over excitation, E_bph > Vpb Ebph

p.f. is leading in nature.

E_Rph ^ Ia_ph = θ      

V_ph ^ Ia_ph = ϕ

The phasor diagram is shown in the Fig. 4.12.2.

Applying cosine rule to ∆ OAB,

But θ + ϕ is generally greater than 90°

cos (θ + ϕ) becomes negative, hence for leading p.f., E_bph > V_ph. 

Applying sine rule to ∆ OAB,

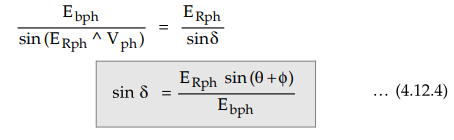
Hence load angle δ, can be calculated once E_bph is known.

Case iii] Critical excitation

In this case  E_bph ≅ V_ph, but p.f. of synchronous motor is unity.

cos ϕ = 1

ϕ = 0^o

i.e. V_ph and I_aph are in phase.

and E_{Rph Λ} I_aph  = θ

Phasor diagram is shown in the Fig.4.12.3.

Applying cosine rule to ∆ OAB,

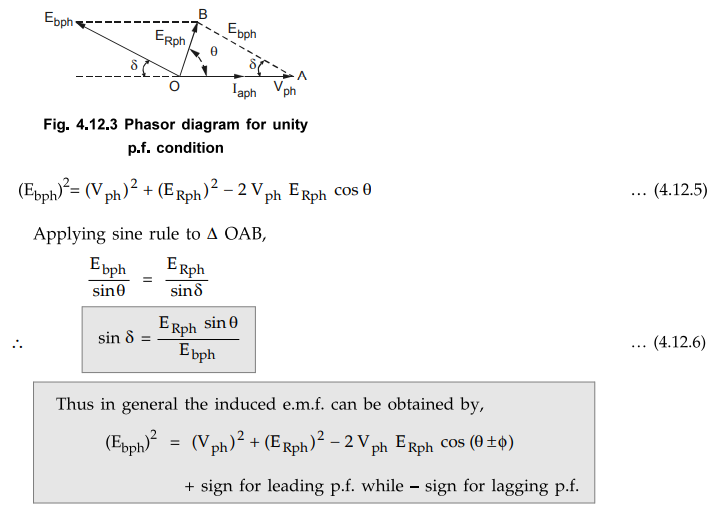
Thus in general the induced e.m.f. can be obtained by,

(E_bph)² = (V_ph)² + (E_Rph)² - 2 V_ph ERph cos (θ ± ϕ)

+ sign for leading p.f. while - sign for lagging p.f.

Example 4.12.1 A 3 phase 11000 V, star connected synchronous motor takes a load of 100 A. The effective synchronous reactance and resistance per phase are 30 Ω and 0.8 Ω respectively. Find the power supplied to the motor and the induced EMF for

1) 0.8 p.f. lag 2) 0.8 p.f. lead.

Solution :

V_L = 11000 V, I_L = 100 A, R_a = 0.8 Ω, X_s = 30 Ω

Example 4.12.2 A 3300 V, delta connected motor has a synchronous reactance per phase of 18 Ω. It operates at a leading power factor of 0.707 when drawing 800 kW from the mains. Calculate its excitation e.m.f. AU : May-2016, Marks 8

Solution : V_L = 3300 V, delta, cos ϕ = 0.707, X_S = 18 Ω , P_in = 800kW

P_in = √3 V_L I_L cos ϕ  i.e. I_L  = 800 × 103 / √3 × 3300 × 0.707 = 197.97 A

I_aph = I_L / √3 = 114.3 A   … delta

As power factor is leading,

Example 4.12.3 A 3 phase, 500 V, synchronous motor draws a current of 50 A from the supply while driving a certain load. The stator is star connected with armature resistance of 0.4 Ω per phase and a synchronous reactance of 4 Ω per phase. Find the power factor at which motor would operate when the field current is adjusted to give the line values of generated e.m.f. as i) 600 V and ii) 380 V

Solution : V_L = 500 V star connection

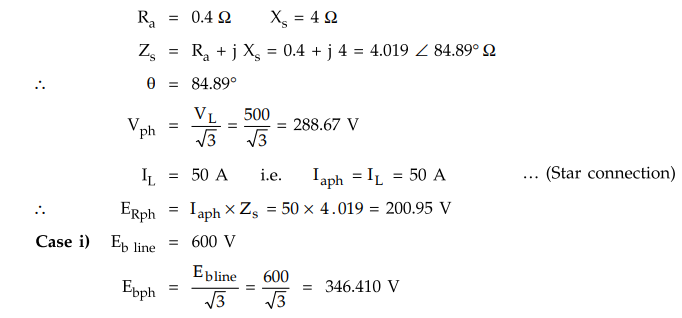
E_bph > V_ph , hence motor is over excited and the power factor will be leading. For leading power factor,

Examples for Practice

Example 4.12.4 A 400 V, 3 phase, star connected synchronous motor has an armature resistance of 0.2 Ω per phase and synchronous reactance of 2 Ω per phase. While driving a certain load, it takes 25 A from the supply. Calculate the back e.m.f. induced in the motor if it is working with i) 0.8 lagging ii) 0.9 leading and iii) Unity power factor conditions.

[Ans.: i) 200.505 V ii) 252.562 V iii) 231.38 V]

Example 4.12.5 A three phase, 6600 V, star connected synchronous motor delivers 500 kW power to the full load. Its full load efficiency is 83 %. Its armature resistance is 0.3 Ω per phase and synchronous reactance is 3.2 Ω per phase. It is working with 0.8 leading power factor on full load. Calculate : i) generated e.m.f. on full load, ii) the load angle.

[Ans.: i) 3925.31 V ii) δ = 2.63°]

Example 4.12.6 A 2300 V, 3-phase, star-connected synchronous motor has a resistance of 0.2 Ω per phase and a synchronous reactance of 2.2 Ω/phase. The motor is operating at (0.5 p.f.) leading with a line current of 200 A. Determine the value of the generated e.m.f. per phase.

[Ans.: 1708.012 V]

Review Questions

1. Derive the expression for induced e.m.f. per phase in a synchronous motor.

2. Draw and explain the phasor diagram of a cylindrical rotor synchronous motor operating at different power factors.