First Order High Pass Butterworth Filter using Op-amp

First Order High Pass Butterworth Filter

As mentioned earlier, a high pass filter is a circuit that attenuates all the signals below a specified cut off frequency denoted as fL. Thus, a high pass filter performs the opposite function to that of low pass filter. Hence, the high pass filter circuit can be obtained by interchanging frequency determining resistances and capacitors in low pass filter circuit.

The first order high pass filter can be obtained by interchanging the elements R and C in a first order low pass filter circuit. The Fig. 3.8.1 shows the first order high pass Butterworth filter.

It can be observed that as compared to first order low pass filter (Fig. 3.4.1), the positions of R and C are changed in the high pass circuit shown in Fig. 3.8.1. 

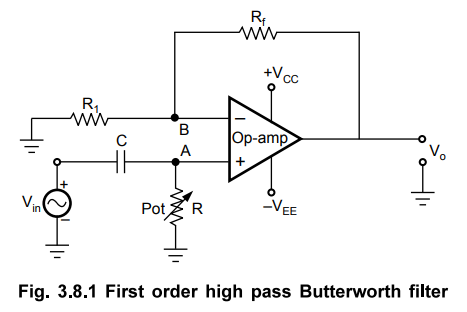
The frequency at which the gain is 0.707 times the gain of filter in pass band is called low cut-off frequency and denoted as f_L. So, all the frequencies greater than f_L are allowed to pass but the maximum frequency which is allowed to pass is determined by the closed loop bandwidth of the op-amp used.

1. Analysis of the Filter Circuit

The impendance of the capacitor is – jX_C = -j (1 / 2π f C) where f is the input i.e. operating frequency.

By the voltage divider rule, the potential of the non inverting terminal of the op-amp is,

This is the required expression for the transfer function of the filter.

For the frequency response, we require the magnitude of the transfer function which is given by,

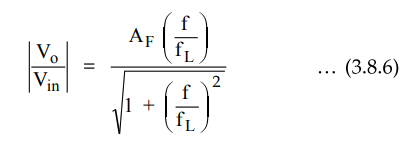
The equation (3.8.6) describes the behaviour of the high pass filter.

1) At low frequencies, i.e. f < f_L

|V_o / V_in| < A_F

2) At f = f_L,

|V_o / V_in| = 0.707 A_F i.e. 3 dB down from the level of A_F

3) At f > f_L, i.e. high frequencies, 1 can be neglected as compared to denominator.

|V_o / V_in|  ≅ A_F i.e. constant

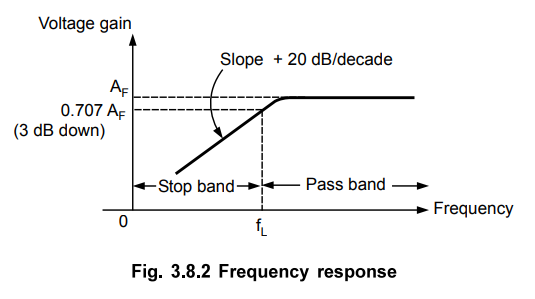
Thus, the circuit acts as high pass filter with a passband gain as AF. For the frequencies, f < f_L, the gain increases till f = f_L at a rate of +20 dB/decade. Hence, the slope of the frequency response in stop band is + 20 dB/decade for first order high pass filter.

The frequency response is shown in the Fig. 3.8.2.

Note As high pass filter is basically a low pass filter circuit with positions of R and C interchanged, the design steps and the frequency scaling method discussed earlier for low pass filter is equally applicable to the first order high pass butterworth filter.

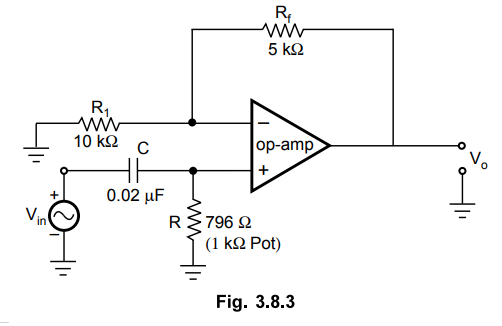
Example 3.8.1 Design a high pass filter with a cut-off frequency of 10 kHz with a passband gain of 1.5.

Solution :

Step 1 : The lower cut-off frequency is 10 kHz. i.e f_L = 10 kHz

Step 2 : Choose C less than 1 µF. hence C = 0.02 µF

Step 3 : Calculate R

The complete circuit is shown in the Fig. 3.8.3.

Review Question

1. Draw and explain the operation of first order high pass butterworth filter.