First Order Low Pass Butterworth Filter using Op-amp

First Order Low Pass Butterworth Filter

The first order low pass butterworth filter is realised by R-C circuit used alongwith an op-amp, used in the noninverting configuration. The circuit diagram is shown in Fig. 3.6.1.

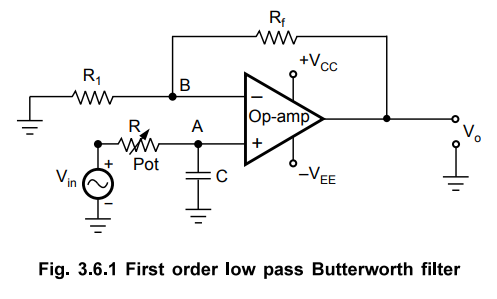
This also called one pole low pass Butterworth filter.

The resistances R_f and R_f decide the gain of the filter in the pass band.

1. Analysis of the Filter Circuit

The impedance of the capacitor C is - jX_C where X_C is the capacitive reactance given by X_C = 1 / 2π f C.

By the potential divider rule, the voltage at the noninverting input terminal A which is the voltage across capacitor C is given by,

The V_o / V_in is the transfer function of the filter and can be expressed in the polar form as

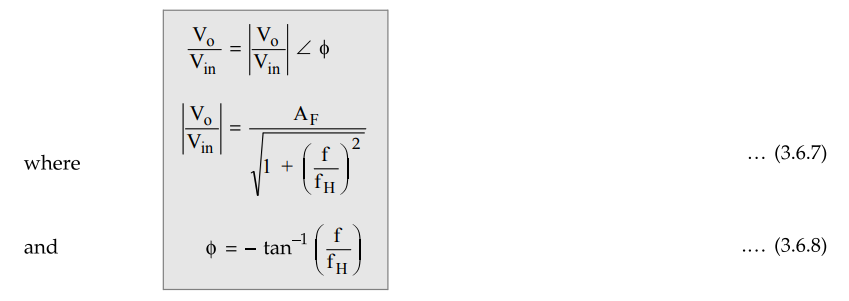
The phase angle ϕ is in degrees.

The equation (3.6.7) describes the behaviour of the low pass filter. 

1. At very low frequencies, f < f_H

Thus, for the range of frequencies, 0 < f < f_H, the gain is almost constant equal to fH which is high cut off ( frequency. At f = f_H, gain reduces to 0.707 A_F i.e. 3 dB down from A_F. And as the frequency increases than f_H, the gain          decreases at a rate of 20 dB/decade. The rate 20 dB/decade means decrease of 20 dB in gain per 10 times change in frequency. The same rate can be expressed as 6 dB/octave i.e. decrease of 6 dB per two times change in the frequency. The frequency f_H is called cut off frequency, break frequency, - 3 dB frequency or corner frequency. The frequency response is shown in the Fig. 3.6.2.

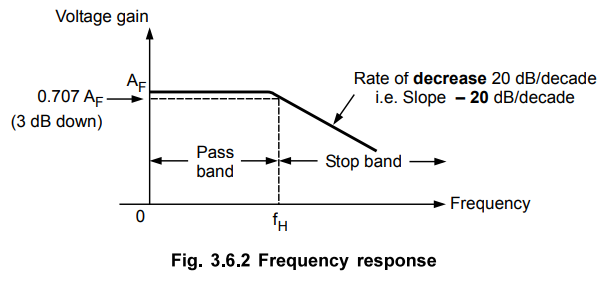
Key Point The rate of decrease in gain is 20 dB/decade i.e. the decrease can be indicated by a negative slope in the frequency response, as - 20 dB/decade.

2. Design Steps

The design steps for the first order low pass Butterworth filter are

1) Choose the cut off frequency, f_H.

2) Choose the capacitance C usually betwen 0.001 and 1 µF. Generally, it is selected as 1 µF or less than that. For better performance, mylar or tantalum capacitors are selected.

3) Now, for the RC circuit,

f_H = 1 / 2 π R C  ... Refer equation (3.6.6)

Hence, as f_H and C are known, calculate the value of R.

4) The resistances R_f and R₁ can be selected depending on the required gain in the pass band.

AF = 1 + R_f / R₁

3. Frequency Scaling

Once the filter is designed, sometimes, it is necessary to change the value of cut-off frequency fH. The method used to change the original cut-off frequency fH to a new cut-off frequency f_H1 is called as frequency scaling.

To achieve such a frequency scaling, the standard value capacitor C is selected first. The required cut-off frequency can be achieved by calculating corresponding value of resistance R. But to achieve frequency scaling a potentiometer is used as shown in Fig. 3.6.1. Thus, the resistance R is generally a potentiometer with which required cut-off frequency f_H can be adjusted and changed later on if required.

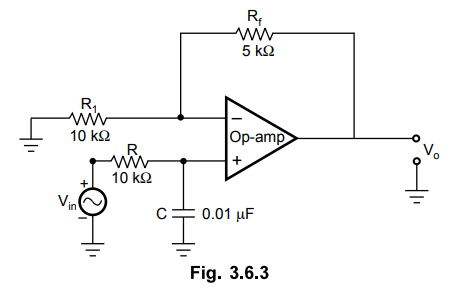
Example 3.6.1 Design a first order low pass filter for a high cut-off frequency of 1 kHz and pass band gain of 2.

Solution :

The designed circuit is shown in the Fig. 3.6.3.

Review Questions

1. Draw the circuit of a first order active low pass filter and derive its frequency response and plot the same.

2. Design a first order low pass filter for cut-off frequency of 2 kHz and pass band gain of 2.

May-13, Marks 8

[Ans.: Refer example 3.4.2 and Verify R_f = R₁ = 10 kΩ, C = 0.001 µF, R = 79.57 kΩ ]