Force between Differential Current Elements

Force between Differential Current Elements

AU : Dec.-05, 07, 08, 09, 12, 13, May-04, 10, 11, 12

• While discussing the electrostatic fields, we have studied that a point charge exerts a force on another point charge, separated by distance R. If these charges are of same type (i.e. both positive or negative), then they repel each other. But when two charges are of different type (i.e. one positive and other negative), then they attract each other.

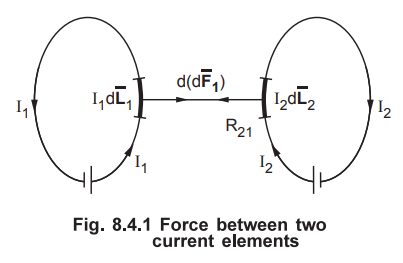
• Let us now consider two current elements 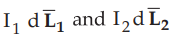 as shown in the Fig. 8.4.1. Note that the directions of I₁ and I₂ are same.

• Both the current elements produce their own magnetic fields. As the currents are flowing in the same direction through the elements, the force d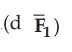 exerted on element  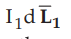due to the magnetic field  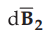produced by other element 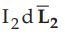 is the force of attraction.

• From the equation of force the force exerted on a diffe rential current element is given by,

p

• According to Biot-Savart's law, the magnetic field produced by current element  is given by, for free space,

p

• The equation (8.4.3) represents force between two current elements. It is very much similar to Coulomb's law. By integrating d (d F2) twice, the total force  on current element 1 due to current element 2 is given by,

• Exactly following same steps, we can calculate the force  exerted on the current element 2 due to the magnetic field  produced by the current element

1. Thus,

• Actually equation (8.4.5) is obtained from equation (8.4.4) by interchanging the subscripts 1 and 2. By using back-cab rule for expanding vector triple product, we can show that

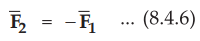
• Thus, above condition indicates that both the forces  obey Newton's third law that for every action there is equal and opposite reaction.

 

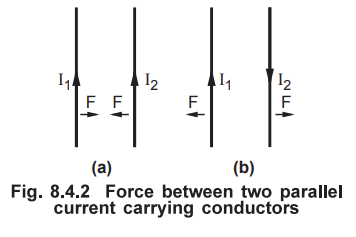
1. Force between Two Parallel Conductors

• Now consider that two current carrying conductors are placed parallel to each other. Each of this conductor produces its own flux around it. So when such two conductors are placed closed to each other, there exists a force due to the interaction of two fluxes. The force between such parallel current carrying conductors depends on the directions of the two currents. If the directions of both the currents are same, then the conductors experience a force of attraction as shown in the Fig. 8.4.2 (a). And if the directions of two currents are opposite to each other, then the conductors experience a force of repulsion as shown in the Fig. 8.4.2 (b).

• Consider two long parallel conductors of length I each placed in a medium. Assume that the conductors are separated by distance d as shown in the Fig. 8.4.3.

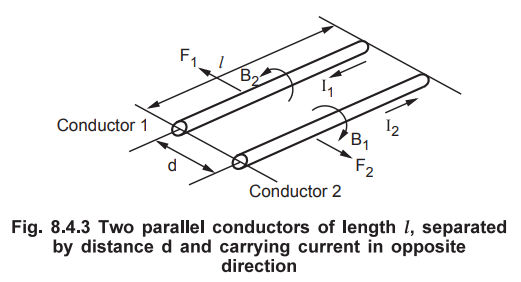
Assume that the conductors carry current in opposite direction as shown in the Fig. 8.4.3.

• Now the magnitude of force exerted on conductor 1 i.e.|  | due to magnetic field  produced by conductor 2 is given by,

• Now using Ampere circuital law, we can find magnitude of magnetic field intensity due to straight long conductor as

H₂ = I₂ / 2πd

Hence by definition,

B₂ = µH₂ = µ₀ µ_r I₂ / 2πd ... (8.4.9)

• Substituting value of B₂ m expression for F₁, we get,

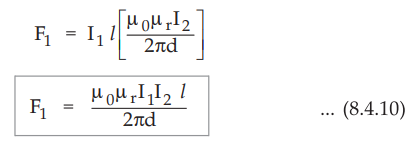
• Similarly the magnitude of force acting on conductor 2 due to magnetic field produced by conductor 1, we can write,

• Thus in general, we can write that, for the two parallel conductors of length I carrying two same or different currents, the force exerted is given by,

• where I₁ and I₂ are the currents flowing through conductor 1 and conductor 2 and d is the distance of separation between two conductors.

• If the two currents flow in same directions, the current carrying conductors attract each other. While if, the two currents flow in opposite direction to each other, the current carrying conductors repel each other.

 

Ex. 8.4.1 A current 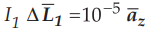element, A.m is located at P, (1,0,0) while a second element, 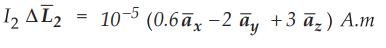 both in free space. Find the vector force exerted on 

Sol. : The magnetic field intensity at point P₁ due to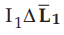 can be obtained using Biot-Savart's law as follows.

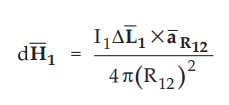
The unit vector in the direction of  is drawn from P₁ to P₂.

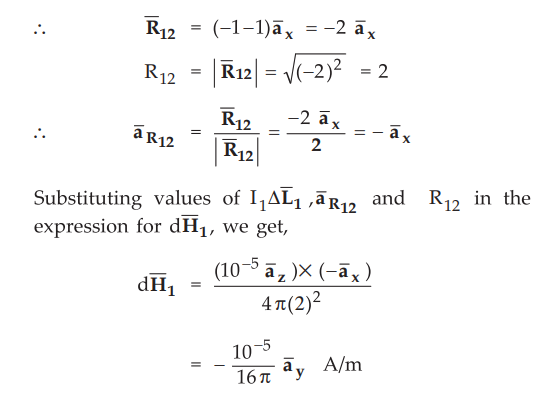
Thus the magnetic flux density at point P₁ is given by,

 

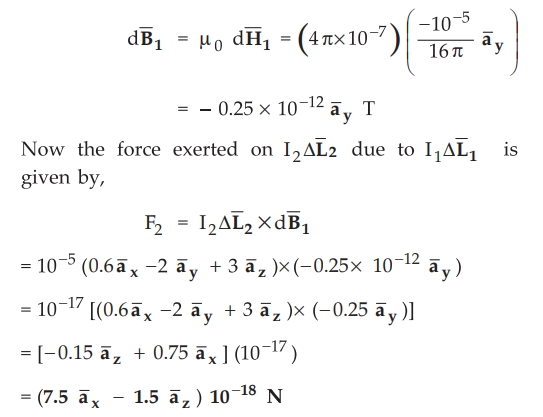
Ex. 8.4.2 Determine the force between two long parallel wires of 200 m length separated by 5 cm in air carrying currents of 40 A in same direction and in opposite direction.

AU : Dec.-08, Marks 4

Sol . :

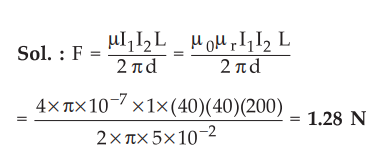
When currents in both conductors are in same direction, the conductor experience force of attraction of 1.28 N. When currents are in opposite direction, the conductors experience force of repulsion 1.28 N.

 

Ex. 8.4.3 Determine the force per meter length between two long parallel wires A and B separated by distance 5 cm in air and carrying currents of 40 A in the same direction.

AU : Dec.-07, 09, Marks 4

Sol. :

The force per meter length L between two long conductors is given by,

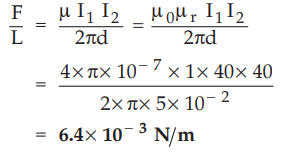
As the currents in both the parallel conductors flow in same direction, the force experienced will be force of attraction.

 

Ex. 8.4.4 Two wires carrying current in the same direction of 3 A and 6 A are placed with their axes 5 cm apart, free space permeability = 4π × 10^-7 H/m. Calculate the force between them in N/m length.

Sol. : Force between two parallel conductors is given by,

F = µI₁ I₂ l / 2πd

d = Distance of separation = 5 cm = 5 × 10^-2m, I₁         = 3 A, I₂ = 6 A, l = Length of conductors

Hence force per unit meter length is given by,

 

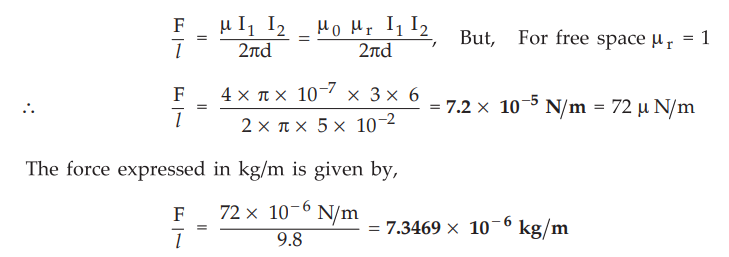
Ex. 8.4.5 The magnetic flux density in a region of free space is given by 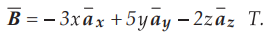. Find the total force on the rectangular loop as shown in the Fig. 8.4.4. If it lies in the plane z = 0 and is bounded by x = 1, x = 3, y = 2, y = 5, all dimensions in cm.

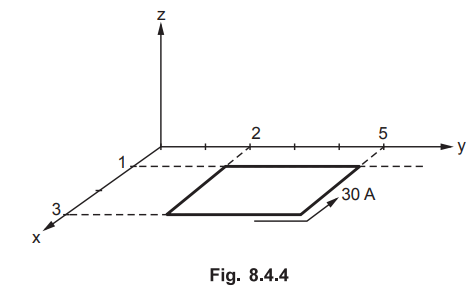
Sol. : In the plane z = 0, the z-component of the magnetic field   will be zero. In other words it will not contribute to the force. The force on the loop is given by,

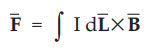
Considering dimensions of all sides in meter, we can write,

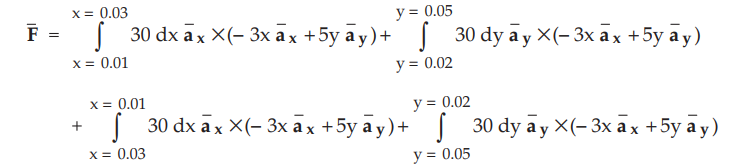
For side 1 and 3, the values of y are 0.02 and 0.05 respectively. While for sides 2 and 4, the values of x are 0.03 and 0.01 respectively.

 

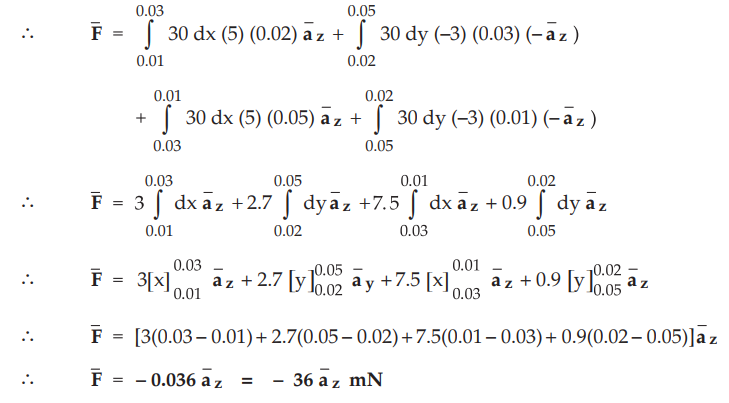
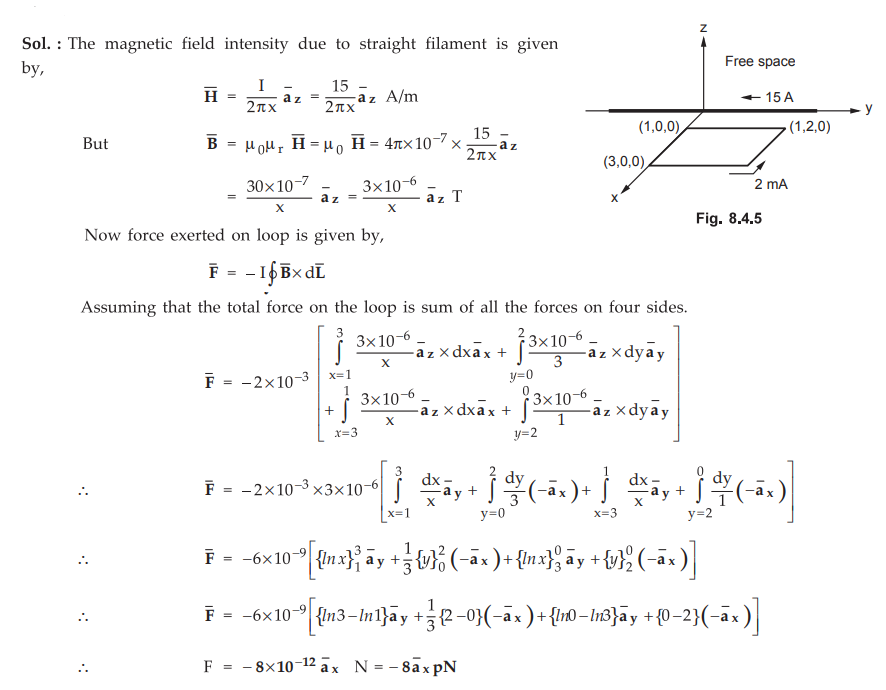
Ex. 8.4.6 Find the force on a wire carrying a current of 2 mA placed in xy plane bounded by x = 1, x = 3, y = 0 and y = 2 as shown in the Fig. 8.4.5. The magnetic field is due to the long conductor, located in y-axis, carrying a current of 15 A as shown.

Sol. : The magnetic field intensity due to straight filament is given by,

 

Examples for Practice

Ex. 8.4.7 Two parallel circular loops of radii, r₁ and r₂ (r₁ >> r₂ ) are coaxially located and carry currents I₁ and I₂ respectively. The axial distance between the centres of loops is 'z'. Find approximately the force between the loops.

Ex. 8.4.8 Find the force per meter length between two long parallel wires separated by 10 cm in air and carrying a current of 10 A in the same direction.

[Ans.: 0.2 mN/m]

Review Questions

1. Derive an expression for the force between two long straight parallel current carrying conductors.

AU : May-10, Dec.-13, Marks 10

2. Establish the relation of force between current carrying parallel conductors.

3. Derive the magnetic force between two parallel conductors carrying equal currents in the i) Same direction ii) Opposite direction