Force on a Differential Current Element

Force on a Differential Current Element

• Practically a differential element of charge is made up of very large number of small and discrete charges. The volume thus occupied by these charge is obviously small but it is effectively greater than the average separation between charges. The differential force given by equation (8.3.1) is the addition of the forces on the individual charges.

• Consider a conductor in which the electrons are in motion. Along with these electrons in motion, the immobile positive ions form a crystalline array structure of a conductor with the magnetic field applied to the conductor, a force is exerted on the electrons and thus their position is slightly shifted. Hence a small displacement is produced between the centers of gravity of positive and negative charges. But this displacement is opposed by Coulomb's forces between positive ions and electrons. So when electrons try to move, the force of attraction between electrons and positive ions is observed. Thus the magnetic force gets transferred to the conductor itself. In good conductor, the Coulomb's forces are much greater than magnetic forces. Thus the separation of charges is observed which indicates that small potential difference exists across conductor in a direction perpendicular to the magnetic field as velocity of charges both. The small voltage across conductor is called Hall voltage and the effect is called Hall effect.

• The concept of Hall effect is used to measure the magnetic flux density. In some applications, the current through device is made proportional to the magnetic field, then the device based on Hall effect can be used as electronic wattmeter and squaring elements. Another application of the Hall effect is observed in the semiconductor physics. In semiconductors, the equal current is provided by holes which are positively charged as well as electrons which are negatively charged. The Hall effect is useful in determining whether the given semiconductor material is p-type or n-type as the Hall voltages for both the materials are different.

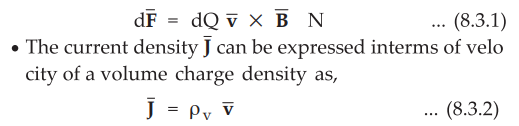
• But the differential element of charge can be expressed in terms of the volume charge density as,

dQ = ρv dv ... (8.3.3)

• Substituting value of dQ in equation (8.3.1),

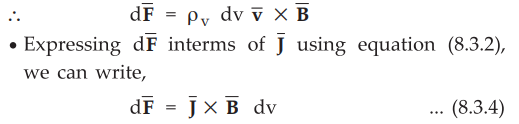
• But we have already studied in previous chapter, the relationship between current element as,

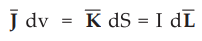
• Then the force exerted on a surface current density is given by,

• Similarly the force exerted on a differential current element is given by,

• Integrating equation (8.3.4) over a volume, the force is given by,

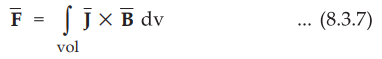
• Integrating equation (8.3.5) over either open or closed surface, we get,

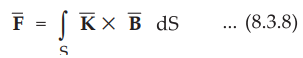
• Similarly integrating equation (8.3.6) over a closed path, we get,

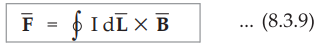
• Note that the magnetic field developed by current element to I  does not exert a force on the element itself similar to a point charge does not exert a force in itself. In other words, the magnetic field   is always external to the current element I .

• If a conductor is straight and the field B is uniform along it, then integrating equation (8.3.6) we get simple expression for the force as,

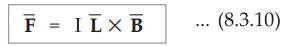
The magnitude of the force is given by,

F = I L B sin θ

• Actually the magnetic field exerts a magnetic force on the electrons which constitutes the current I. But these electrons are part of the conductor, this magnetic force gets transferred to the conductor lattice. Now this transferred force can perform work on a conductor as a whole.

Ex. 8.3.1 A conductor 6 m long, lies along z-direction with a current of 2 A in  direction. Find the force experienced by conductor if .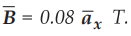

Sol. : A force exerted on current carrying conductor in a magnetic field is given by,

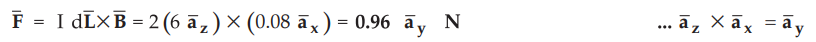
Ex. 8.3.2 A conductor of length 2.5 m in z = 0 and x = 4 m carries a current of 12 A in -  direction. Calculate the uniform flux density in the region, if the force on the conductor is 12 × 10^-2 N in the direction specified by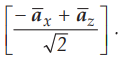 

Sol. :

Ex. 8.3.3 A magnetic field 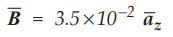 exerts a force on a 0.3 m long conductor along x axis. If a current of 5 A flows in   direction, determine what force must be applied to hold conductor in position.

Sol. : The force exerted on a straight conductor is given by,

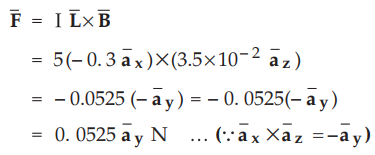
Hence the force applied to hold the conductor in position must be

Examples for Practice

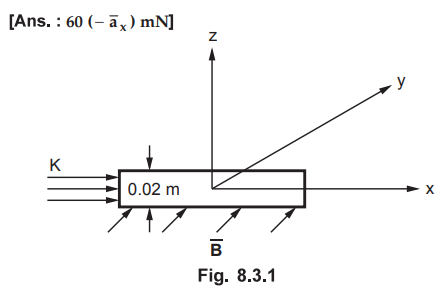
Ex. 8.3.4 A current strip 2 cm wide carries a current of 15 A in  direction, as shown in the Fig. 8.3.1. Find the force on the strip of unit length if the uniform field is  tesla.

 Ex. 8.3.5 A current element 4 cm long is along y-axis with a current of 10 mA flowing in y-direction. Determine the force on the current element due to the magnetic field, if the magnetic field H = [5 ax / µ] A/m.

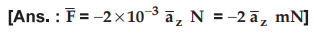
Ex. 8.3.6 A conductor 4 m long lies along the y-axis with a current of 10 A in the  direction. Find the force on the conductor if the field in the region is 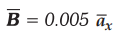 Tesla.

 Review Questions

1. Derive various expressions for force on a differential current element.

2. Write a note on force on a differential current element.