Force on a Moving Point Charge

Force on a Moving Point Charge

AU : Dec.-09, 17

• According to the discussion in the previous chapters, a static electric field  exerts a force on a static or moving charge Q. Thus according to Coulomb's law, the force  exerted on an electric charge can be obtained. The force is related to the electric field intensity  as,

• For a positive charge, the force exerted on it is in the direction of . This force is also referred as electric force (  ).

• Now consider that a charge is placed in a steady magnetic field. It experiences a force only if it is moving. Then a magnetic force ( ) exerted on a charge Q, moving with a velocity  in a steady magnetic field  is given by,

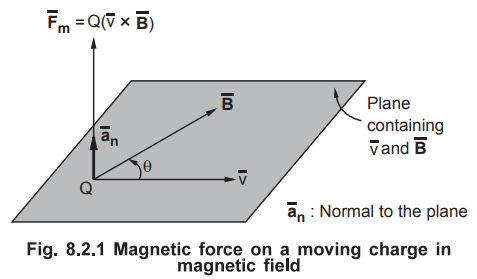
• The magnitude of the magnetic force  is directly proportional to the magnitudes of Q, 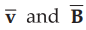  also the sine of the angle between 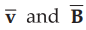. The direction of  is perpendicular to the plane containing 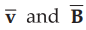 both, as shown in the Fig. 8.2.1.

• From equation (8.2.1) it is clear that the electric force  is independent of the velocity of the moving charge. In other words, the electric force exerted on the moving charge by the electric field is independent of the direction in which the charge is moving. Thus the electric force performs work on the charge. On the other hand, the magnetic force  is dependent on the velocity of the moving charge. But  cannot perform work on a moving charge as it is at right angle to the direction of motion of charge.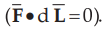 

Lorentz Force Equation : Newton stated important property of two or more forces that they act independently of each other but their net or resultant effect is the sum of the effects of all forces. That means, if a particle carrying charge + Q and moving with velocity   is present in a region where both electric and magnetic fields are present, then the particle in a motion experiences forces 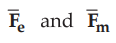 due to the electric and magnetic fields respectively and the resultant force experienced by a charged particle in motion is given by,

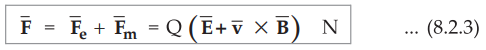
• Above equation is called Lorentz Force Equation which relates mechanical force to the electrical force.

• The important points to be remembered about the Lorentz force equation are,

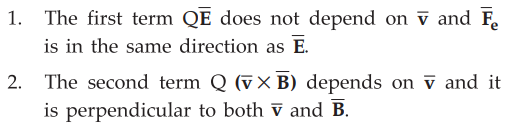
• The name given to equation was in the honour of Dutch Physicist Hendrik A. Lorentz (1853-1928) who was the second person in the word to achieve Nobel Prize for Physics in 1902. The solution of this equation is useful in the determination of electron orbits in magnetron, proton paths in cyclotron and plasma characteristics in Magnetohydrodynamic Generator (MHD generator).

• If the mass of the charge is m, then we can write,

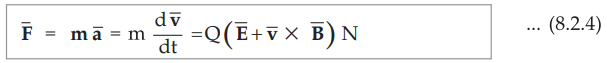
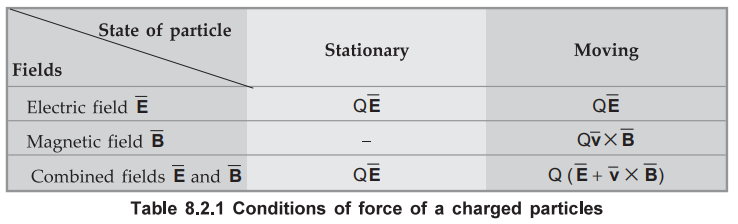
• Let us summarize the important conditions of a force on a charged particle as given in Table 8.2.1.

Key Point : 1. The electric force is exerted on a point charge irrespective of whether it is stationary or in motion. But the magnetic force is exerted on a point charge only if it is in motion.

2. The electric force is always in the direction of the electric field while the magnetic force is always perpendicular to the magnetic field.

3. The electric force displaces a point charge at the cost of energy but no work is done by the magnetic force when a point charge is displaced.

Ex. 8.2.1 A point charge of Q = - 1.2 C has velocity 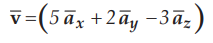 m/s Find the magnitude of the force exerted on the charge if,

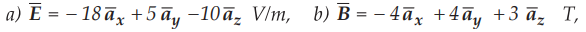
c) Both are present simultaneously.

Sol. : a) The electric force exerted by  on charge Q is given by,

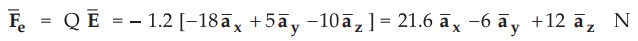
Thus, the magnitude of the magnetic force is given by, 

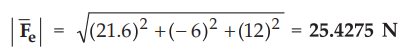
Thus, the magnitude of the total force exerted is given by,

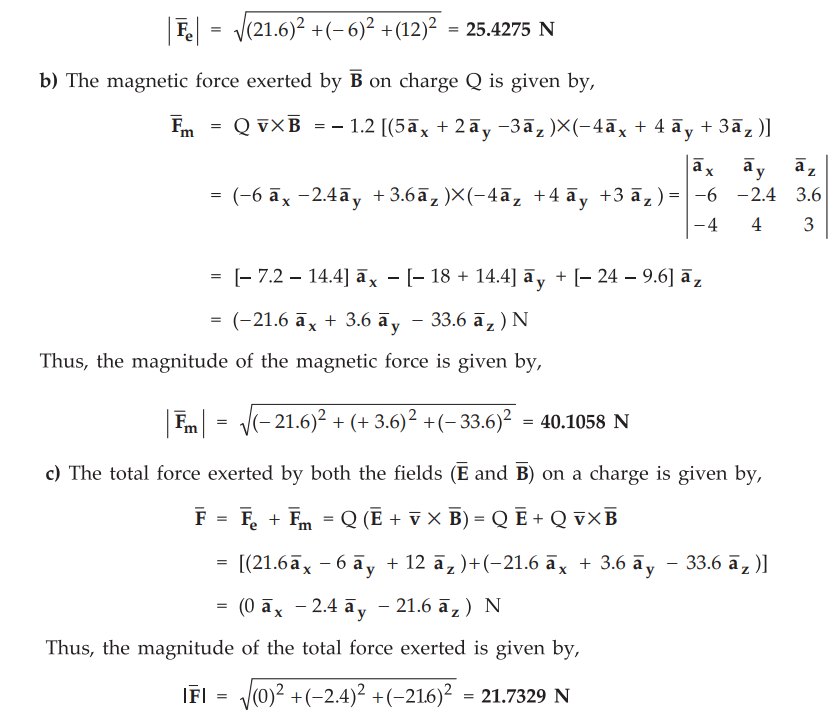
Ex. 8.2.2 A point charge, Q = - 60 nC, is moving with a velocity 6 × 10⁶ mis in the direction specified by unit vector 

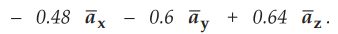
Find the magnitude of the force on a moving charge in the magnetic field,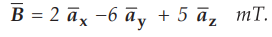

Sol. : The magnitude of velocity is given as v = 6 × 10⁶ m/s. The direction of this velocity is specified by an unit vector. Thus we can write,

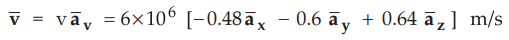
Thus the magnitude of the force on a moving charge is given by,

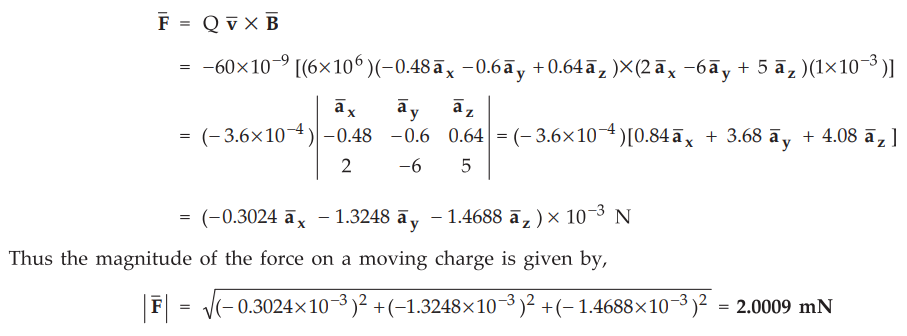
Examples for Practice

Ex. 8.2.3 A charged particle moues with a uniform velocity 4ax m/sec in a region where  Determine Bo such that the velocity of the particle remains constant.

[Ans.: 5 Wb/m²]

Ex. 8.2.4 A charge of Q = 5 × 10^-18 C is    moving through a uniform magnetic field of

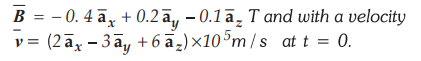
a) What is the electric field present at t = 0 if the net force on the electron is zero ?

b) If the electric field intensity is in the  direction entirety, find E_x if |F_total| = 2 pN.

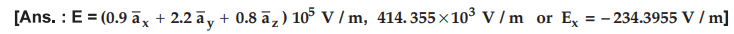
Ex, 8,2.5 A point charge Q = 18 nC has a velocity of 5 × 10⁶ m/s in the direction

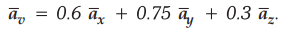
Calculate the magnitude of the force exerted on the charge by the field,

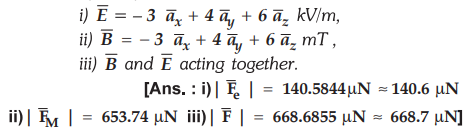
Ex. 8.2.6 If the magnetic field is 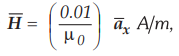 what is the force on a charge of 1 pC moving with a velocity of 10^-6  m/sec.

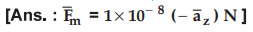
Review Questions

1. Give short note on the following : Lorentz law of force.      

AU : Dec.-09, Marks 4

2. Derive Lorentz force equation.      

3. Define Magnetic force.        

AU : Dec.-17, Marks 2