Form Factor and Crest Factor

FORM FACTOR AND CREST FACTOR

Form factor is defined as the ratio between RMS value and average value.

Form factor = RMS value / Average value ... (8)

Crest or peak factor is defiend as the ratio between maximum value and RMS value.

Crest (peak) factor = Maximum value / RMS value … (10)

 

EXAMPLE 6: Find the RMS value of the sine wave shown in figure.

Solution:

 

EXAMPLE 7: Find the RMS value of the (i) full rectified and (ii) half-rectified sine waves shown in figure.

Solution:

 (i) Full rectified sine wave

(ii) Half rectified sine wave

 

EXAMPLE 8: Find the average and effective values of the saw-tooth waveform shown in figure.

Solution:

 

EXAMPLE 9: Find the form factor and peak factor for the voltage waveform shown in figure.

Solution:

Form Factor = RMS value / Average value'

Peak Factor = Maximum value / RMS value

Since the wave is symmetrical, the average value is found over half a cycle (i.e.  upto T/2)

Area value = Area of the waveform under half the cycle / Period

Area of the waveform under half the cycle = Area of ΔOAB + Area of ΔCDE + Area of Rectangle ACDB

Area of ΔOAB = 1/2 bh = 1/2 × T/8 × 50 = 3.125 T

Area of ΔCDE = 1/2 bh =1/2 × T/8 × 50 = 3.125 T

Area of rectangle ΔCDB = b × h = T/4 × 50 = 12.5 T

Area of the waveform under half the cycle = 3.125 T + 3.125 T + 12.5 T = 18.75 T

Average value = 18.75 T / (T/ 2)  = 37.5 V

Average value = 37.5 V

RMS value = √Area of the squared wave / Period

 

EXAMPLE 10: Calculate the form factor and peak factor of the current wave of period 10 secs, having the following wave shape.

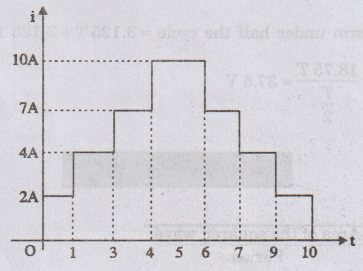
Solution :

 

EXAMPLE 11: Find the average, RMS, form factor and peak factor of the following waveform.

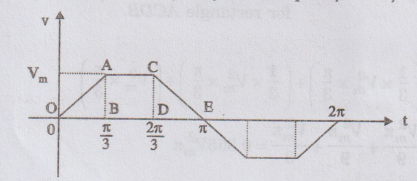
Solution:

Average value: The given waveform is symmetrical. Therefore, the average value is found over half cycle.

 

EXAMPLE 12: An alternating voltage is given by v = 310 sin 314t. Calculate (i) frequency (ii) period (iii) maximum value (iv) RMS value

Solution:

(i) Alternating voltage equation v = 310 sin 314t

EXAMPLE 13: A voltage wave has variations as shown in figure below. Find the average and effective values of the voltage.

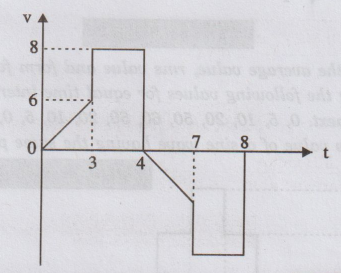
Solution:

Since the wave is symmetrical, the average value is found over half a cycle. (ie, upto 4 s)

Average value

Average value = Area of the wave under half the cycle / Period

Area of the wave under the half cycle = Area of triangle + Area of rectangle

Area of triangle = 1/2 bh = 1/2 × 3 × 6 = 9

Area of rectangle = b × h = 1 × 8 = 8

Average value = 9+8 / 4 = 17/4 = 4.25 V

Average value =  4.25 V

RMS Value

 

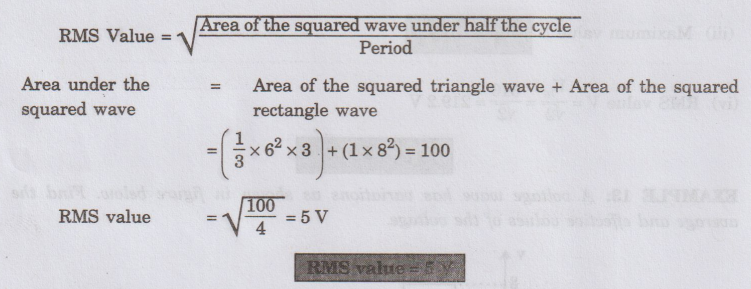
EXAMPLE 14: Find the average value, rms value and form factor and peak factor of a periodic wave having the following values for equal time intervals changing suddenly from one value to the next. 0, 5, 10, 20, 50, 60, 50, 20, 10, 5, 0, -5, -10, etc. What would be the rms value of a sine wave having the same peak value?

Solution:

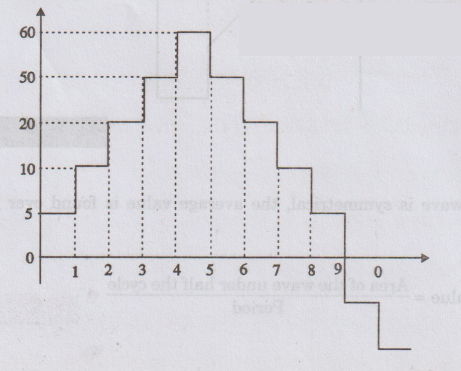
Figure shows the periodic waveform for given values.

This waveform is symmetrical. The average value is found over half a cycle.

Average value = Area of the wave under half the cycle / Period

 

EXAMPLE 15: Compute the RMS value of the current waveform given in figure.

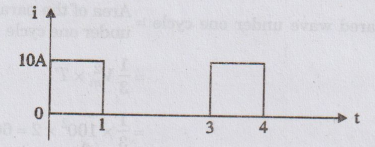
Solution:

Here, the current waveform is unsymmetrical (i.e.,) we have to consider full cycle.

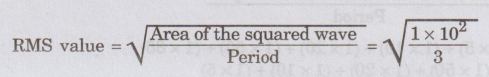
RMS value = 5.77 A

 

EXAMPLE 16: Find the average and effective values of the sawtooth wave shown in figure. Also find the form factor and crest factor.

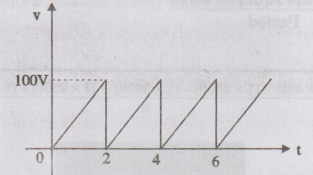
Solution:

RMS value = 57.73 V

Form factor = RMS value / Average value = 57.73 / 50

Form factor = 1.1546

Crest factor = Maximum value / RMS value = 100 / 57. 73 = 1.732

Crest factor = 1.732