Four Quadrant Variable Transconductance Multiplier Circuit

Four Quadrant Variable Transconductance Multiplier Circuit

AU : May-05, 18, Dec.-12, 14

The heart of the four quadrant variable transconductance multiplier circuit is the linearized transconductance multiplier and the differential V-I converter. Let us study these two circuits in brief.

1. Linearized Transconductance Multiplier

This circuit consists of a differential pair of transistors Q₃ - Q₄ to provide a variable transconductance and the transistors Q₁ - Q₂ used as diode with base-collector shorted. This is shown in the Fig. 4.9.1.

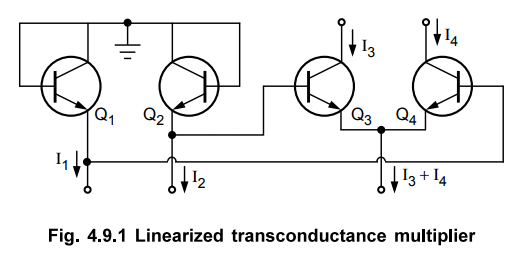
Applying KVL to the pair Q₁ - Q₂ and Q₃ - Q4

V_BE1 + V_BE4 = V_BE2 + V_BE3

i.e. V_BE3 - V_BE4 = V_BEI  - V_BE2 …. (4.9.1)

For the two matched transistors, the change in VBE is proportional to the log ratio of their currents. Hence,

Key Point : Thus current multiplies the differential current (I₁- I₂) by total emitter current (I₃+ I₄)

To get (I₁- I₂) and (I₃- I₄) from the input voltages V1 and V2, two V-I converters are necessary and to convert (I₃- I₄) to the output voltage V_o, one I-V converter is must.

2. Differential V-I Converter

To convert input voltages to get differential current, V-I converter circuit is used as shown in the Fig. 4.9.2. 

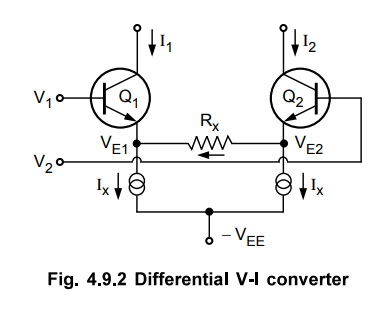
Ignoring the two base currents and applying KCL we get,

Key Point Thus circuit performs V-I conversion.

The linearized transconductance multiplier operates only over two quadrants. Hence using little modifications and using differential V-I converter, the four quadrant variable transconductance multiplier circuit is obtained in practice.

3. Four Quadrant Multiplier Circuit

The Fig. 4.9.3 shows the complete four quadrant variable transconductance multiplier circuit. It uses two linearized transconductance pairs with bases driven in antiphase. The emitters are driven by V-I converters.

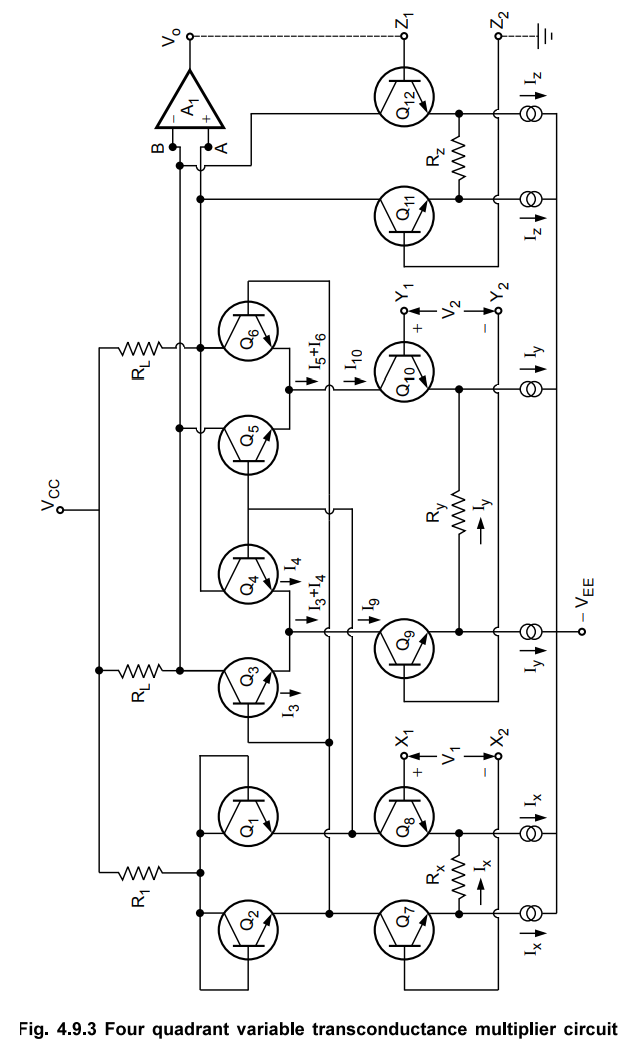
We have derived earlier that for linearized transconductance multiplier circuit,

But the transistors Q₉ and Q₁₀ form another V-I converter for which we can write, referring to the equation (4.9.13) as,

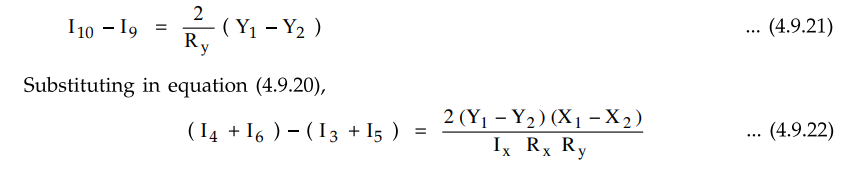
The op-amp A1 alongwith the third V-I converter of transistors Q11 and Q12, form the output I-V converter. The V-I converter of Qn and is in the feedback path of op-amp A₁.

Applying KVL we can write,

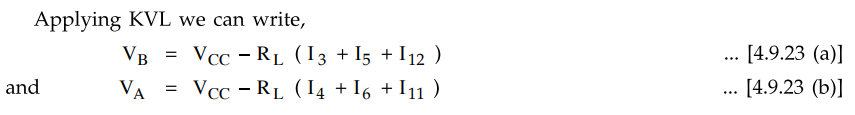
But for an op-amp, the two input terminals are always at same potential i.e. (V_A =V_B). 

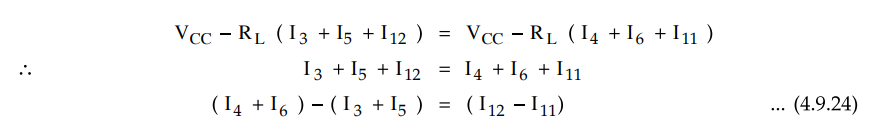
But as Q₁₁ and Q₁₂ form another V-I converter, referring to the equation (4.9.13) we can write,

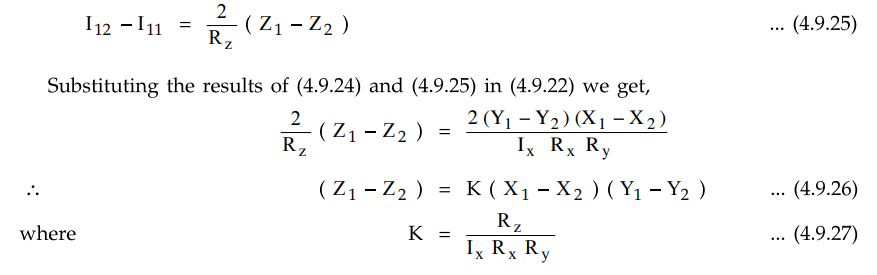
Generally K is selected as (1 / 10) and thus the equation (4.9.27) shows that the circuit functions as a four quadrant multiplier circuit.

So let V₁ = X ₁ - X₂

and    V₂ = Y₁ - Y₂

while V_o = Z₁- Z₂

hence V_o = K V₁V₂  … (4.9.28)

The Fig. 4.9.4 shows the four quadrant transfer characteristics of the transconductance multiplier

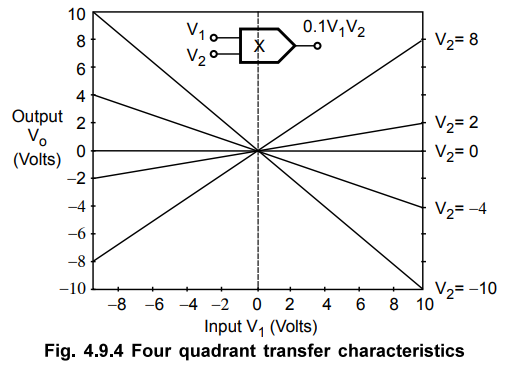
circuit shown in the Fig. 4.9.4, with value of the constant K as 0.1.

The logarithmic term neglected in the V-I converter analysis may be the main cause of error but it is compensated by introducing equal and opposite logarithmic term by means of third V-I converter  of Q₁₁ - Q₁₂ which is in the feedback path.

For maximum flexibility, the resistances R₁ R_L, R_x, R_y and R_z have been left external to the circuit. This is used to vary the scale factor K and common mode ranges of the circuit independently.

This circuit is commonly used for monolithic IC realization and available in monolithic form from variety of manufacturers. The two popular examples of four quadrant multiplier IC are AD 534 by Analog Devices and MPY 100 by Burr-Brown.

Review Question

1. Explain, with necessary equations, the basic circuits of 'Linearized transconductance multiplier' and differential V-I converter' Hence explain the 'Four quadrant variable transconductance multiplier' circuit.