Gauss's Law Applied to Differential Volume Element

Gauss's Law Applied to Differential Volume Element

 Uptill now we have considered the various cases n which there exists a symmetry and component of 

 is normal to the surface and constant everywhere on the surface. But if there does not exist a symmetry and Gaussian surface can not be chosen such that normal component of  is constant or zero everywhere on the surface, Gauss's law cannot be directly applied.

• In such a case a differential closed Gaussian surface is considered. The closed surface is so small that  is almost constant everywhere on the surface. Finally results can be obtained by decreasing the volume enclosed by Gaussian surface to approach to zero.

• Consider a cartesian co-ordinate system and a point P in it such that the electric flux density at P is given by,

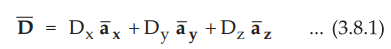
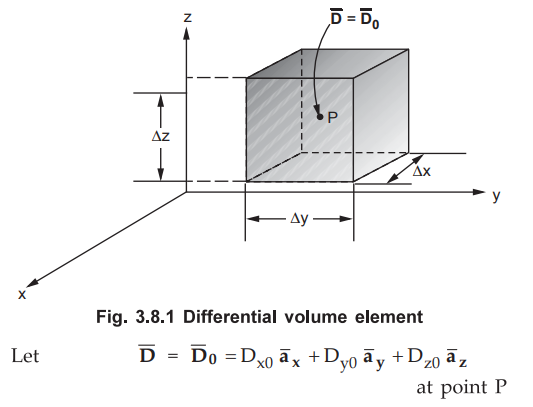
• Consider the closed Gaussian differential surface in the form of rectangular box, which is a differential volume element. The sides of this element are Δx, Δy, and Δz. The position of this element is such that the point P is at the centre of the element and treated to be origin. Hence  at P can be denoted as 0. This is shown in the Fig. 3.8.1.

• The components D_x0, D_y0 and D_z0 vary with distance in the respective directions.

• According to Gauss's law,

• The total surface integral is to be evaluated over six surfaces front, back, leftside, rightside, top and bottom.

• Consider the front surface of the differential element. Though  is varying with distance, for small surface like front surface it can be assumed constant.

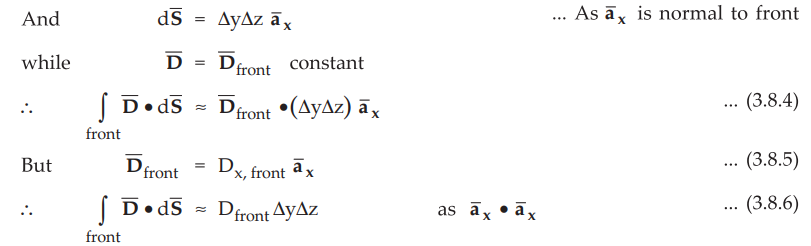
It has been mentioned that D _{x, front} is changing in x direction. At P, it is D_x0 while on the front surface it will change and given by,

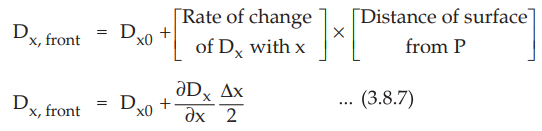
• The point P is at the centre so distance of surface in x direction from P is Δx / 2

• The rate of change is expressed as partial derivative as D_x varies with y and z co-ordinates also.

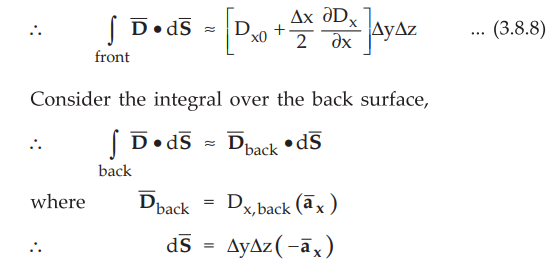
Key Point : Note that the flux is entering from back side and leaving from front in positive x direction hence While the surface considered from point P is in negative x direction hence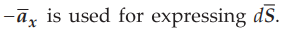  

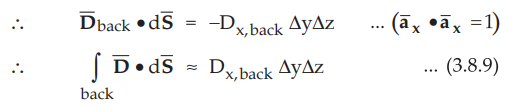
• Now D_x,back is changing with x. At P it is D_x0 while on the back side it will be different and can be obtained as,

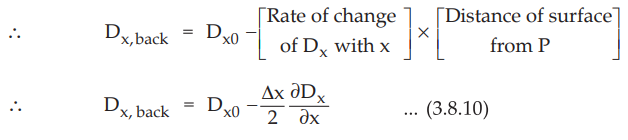
• The negative sign is used as the surface is in negative direction of x from P. Substituting in (3.8.9) we get,

• This result leads to the concept of divergence.

1. Divergence

• Applying Gauss's law to the differential volume element, we have obtained the relation,

Q = (∂D_x / ∂x + ∂D_y / ∂y + ∂Dz / ∂z) Δv

• This is the charge enclosed in the volume Δv.

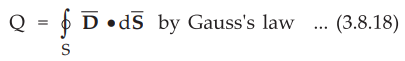
• To apply Gauss's law, we have assumed a differential volume element as the Gaussian surface, over which  is constant. Hence equations (3.8.17) and (3.8.18) can be equated in limiting case as Δv → 0.

• The relations are frequently required in the engineering electromagnetics.

Review Question

1. Explain the Gauss's law as applied to the differential volume element. Hence define divergence of a vector field.