Generalised Circuit Constants of a Transmission Line

Generalised Circuit Constants of a Transmission Line

AU: Oct.-01, May-04, 11, 15, Dec.-03, 04, 06, 10, 11, 13

Consider a two port network shown in the Fig. 2.9.1.

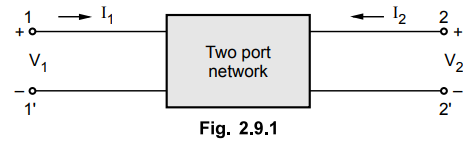
The above network is a four terminal network with 4 variables;

two on input side and two on output

 side. V₁ and I₁ are the voltage and current on input side whereas V₂ and I₂ are the voltage and current on output side.

The transmission system can also be assumed to be a four terminal network with two input terminals where power enters the network and two output terminals where power leaves the network.

Let     V_S = Sending end voltage, I_S = Sending end current

V_R = Receiving end voltage, I_R = Receiving end current

The sending end voltage and current can be expressed in terms of receiving end voltage and current through the set of parameters known as transmission line parameters or ABCD parameters. Thus we have,

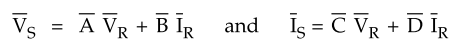
The network between the transmission line should be linear, passive and bilateral. The parameters 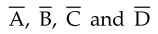 which are generally complex numbers are the constants also known as generalised circuit constants. The method which is used for analysis of transmission line has influence on these constants. With the knowledge of these constants, performance calculations of the line can be easily obtained.

These parameters are given by

Now we will find these constants in case of short and medium transmission line.

 

1. Condition of Symmetry for Transmission Parameters

The basic equations for the transmission parameters are as following, 

 

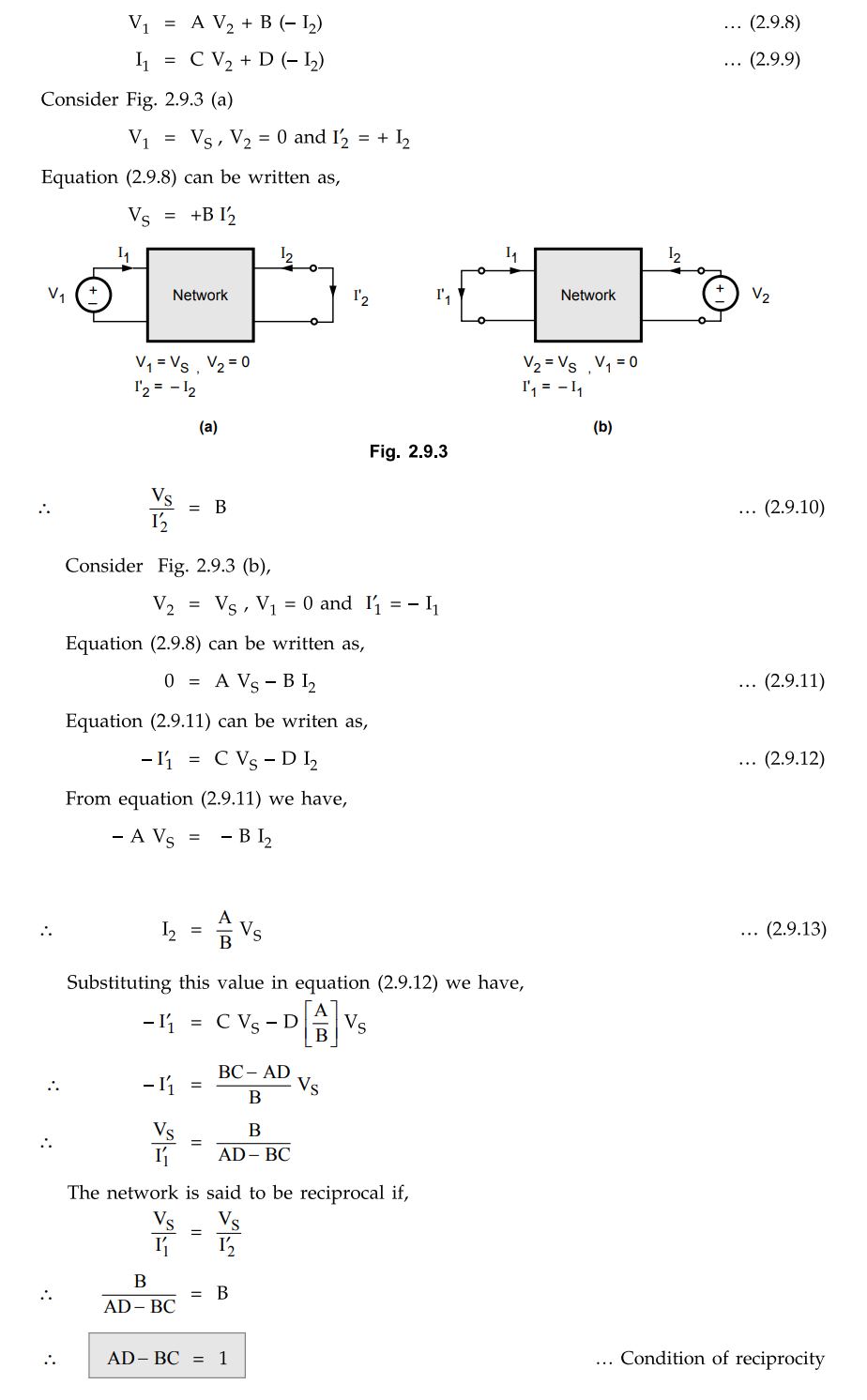
2. Condition of Reciprocity for ABCD Parameters

The basic equations for ABCD parameters are as follows,

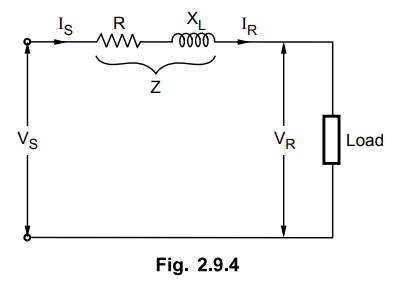
3. Short Transmission Line

The short transmission line is represented in the Fig. 2.9.4. In case of short transmission line, the effect of the line capacitance is neglected. The line is having the series impedance. In the figure only one phase is shown from the three phases.

We have,

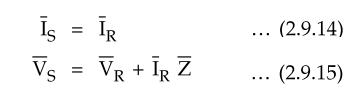
The defining equations for transmission line parameters are

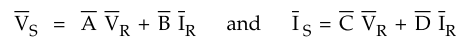
Comparing equations (2.9.14) and (2.9.15) with the standard equations written above we have

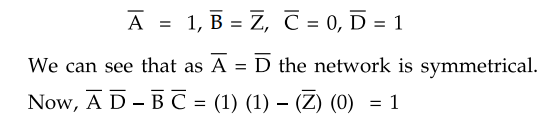
Thus the network is seen to be reciprocal also.

 

4. Medium Transmission Line

a.  Nominal T Method

In nominal T method of analysis of medium transmission line the total line capacitance is assumed to be lumped or concentrated at the center point of the line whereas half the line resistance and reactance are lumped on either side of the line. This is shown in the Fig. 2.9.5.

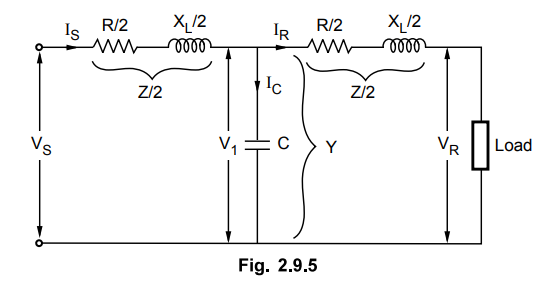
The network is seen to be reciprocal also.

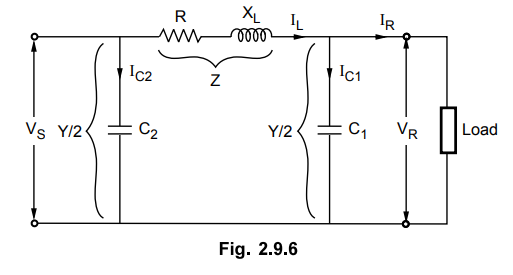
b.  Nominal π Method

In nominal π method, the total capacitance is divided into two halves with one half at the receiving end and the other half at the sending end. This is shown in the Fig. 2.9.6.

 

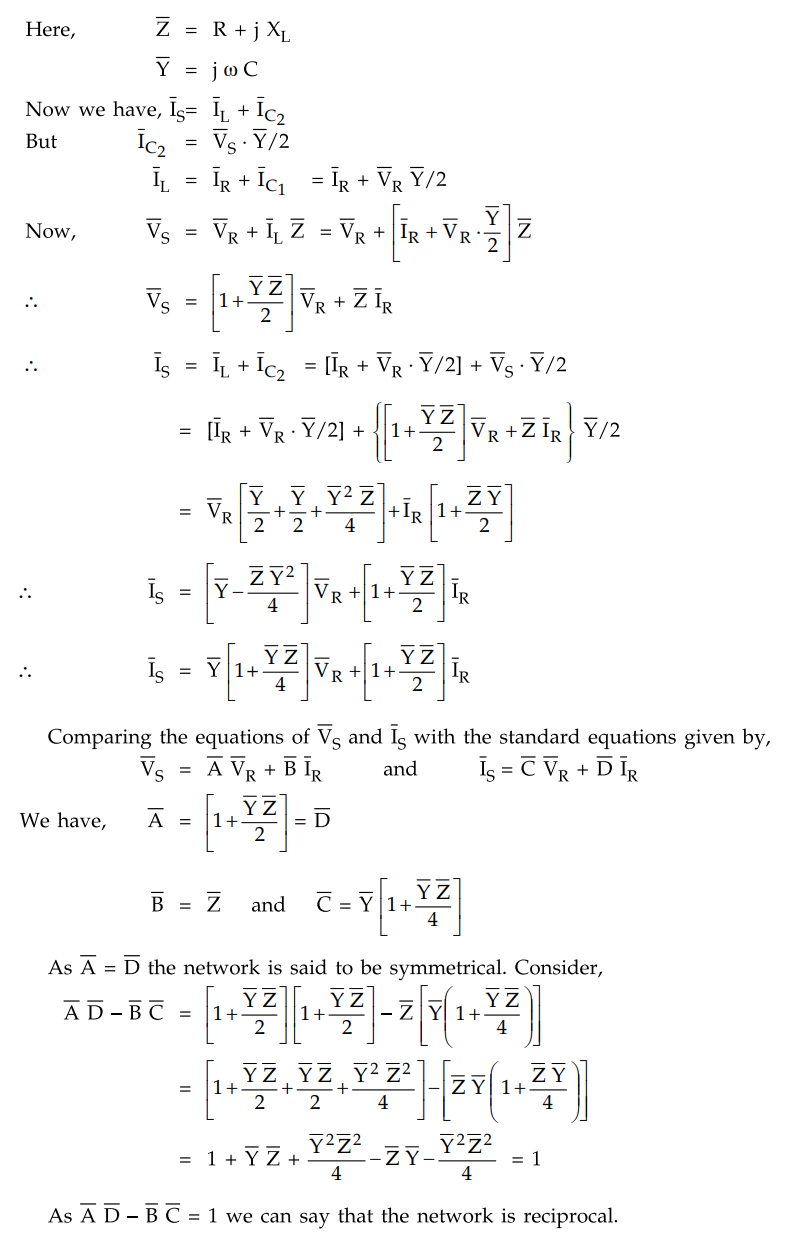
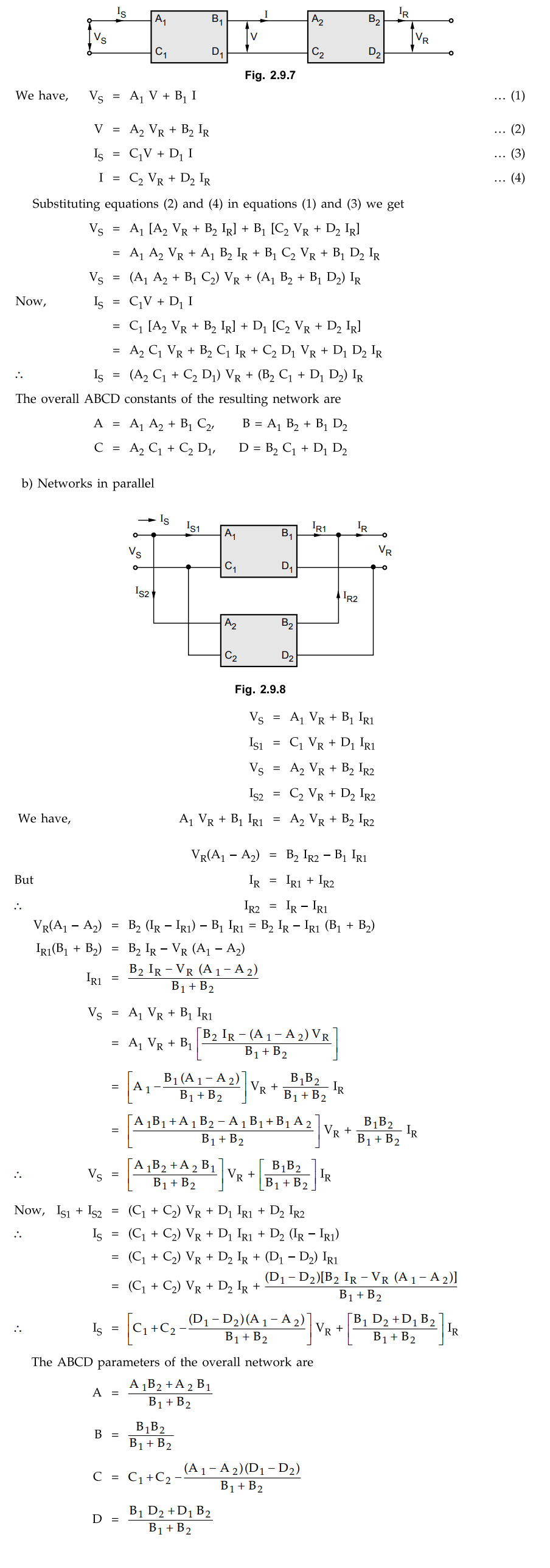
Example 2.9.1 Two transmission lines having generalised circuit constants A₁ , B₁, C₁, D₁ and A₂, B₂, C₂, D₂ are connected in a) series b) parallel.

Derive expression for overall ABCD constants of the resulting network.

Solution : a) Networks in series

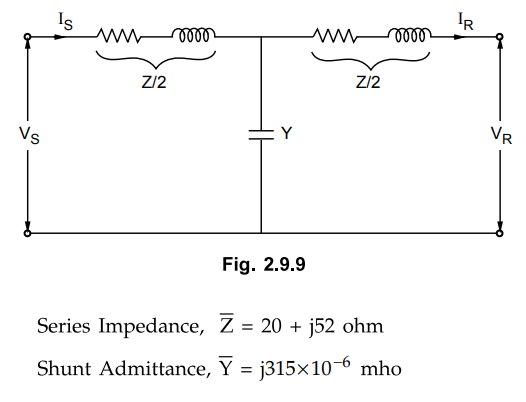
Example 2.9.2 A balanced. 3 phase load of 30 MW is supplied at 132 kV, 50 Hz and 0.85 p.f. lagging by means of a transmission line. The series impedance of a single conductor is (20 + j 52) Ω and the total phase-neutral admittance is 315 x 10_6 mho. Using nominal T method determine :

i) The A, B, C and D constants of the line ii) Sending end voltage iii) Regulation of the line.

Solution : Fig. 2.9.9 shows a representation of a transmission line using nominal T method.

Now ABCD constants of a transmission line are given by,

Receiving end voltage V_R is taken as reference

Sending end voltage per phase = 82.516 kV

Sending end line voltage = √3 × 82.516 = 142.92 kV

Voltage regulation is nothing but change in voltage at receiving end from no load to full load. 

Voltage regulation = 9.168 %

 

Example 2.9.3 A 110 kV, 50 Hz, 3 phase transmission line delivers a load of 40 MW at 0.85 lagging p.f. at the receiving end. The generalised constants of the transmission line are

A = D = 0.95∠ 1.4°

B = 96 ∠ 78° ohm

C = 0.0015 ∠ 90° mho

Find the regulation of the line and charging current use nominal T method.

Solution : Receiving end voltage, V_R = 110 kV

 

Example 2.9.4 The generalised circuit constants of a transmission line are

A = 0.93 + j 0.016

B = 20 + j 140

The load at the receiving end is 60 MVA, 50 Hz at 0.8 p.f. lagging. The voltage at the supply end is 220 kV. Determine the load end voltage.

Solution : Given that,

V_S = 220 kV 220

Phase value,V_S =  220 / √3 = 127 kV

Let the receiving end voltage per phase V_R which is taken as reference vector

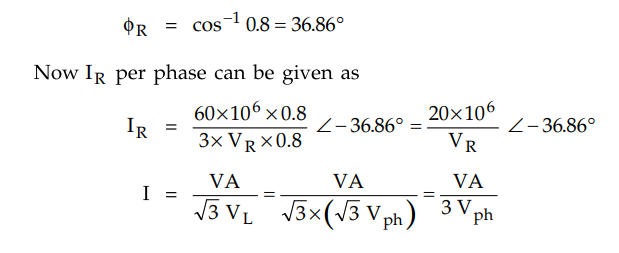
As VR is phase voltage while calculating I, factor 3 is used in the denominator.

Now we have B = 20 + j 140 = 141.421 ∠ 81.8698

The sending end voltage is given by,

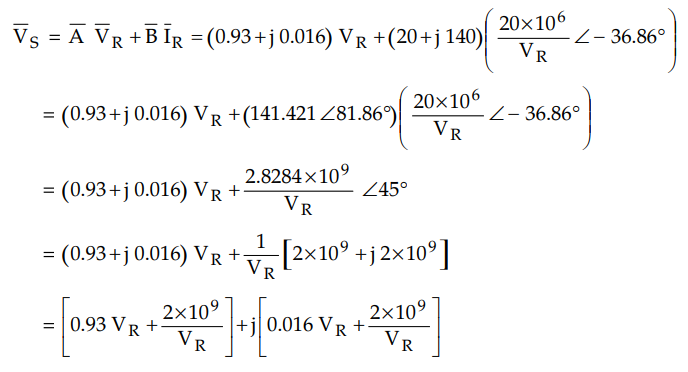
Although we are not knowing the angle associated with V_S we will consider only magnitude of V_S. |V_S| = 127 kV per phase.

Review Questions

1. What are ABCD constants ?

2. Determine the generalized circuit constants of short transmission line. State the characteristics of it. Also prove that short transmission line behaves like a symmetrical network.

3. Derive the relationship between sending end and receiving end quantities in terms of voltage and current for 'Tee' circuit medium transmission line.

4. Express the relationship for the sending end voltage and current in terms of receiving end voltage and current for a medium length transmission line with nominal pi method of representation. Evaluate the generalised circuit constants.

5. Determine the generalized circuit constants of medium transmisison line. Also prove that the transmission line behaves like a symmetrical network and reciprocal network.

6. Derive an expression for ABCD constants of a medium transmission lines using nominal T method. Show that AD - BC = 1.

7. Derive the values of generalised network constants A, B, C and D using nominal n equivalent circuit for medium transmission line.

8. A balanced 3 phase load of 30 MW is supplied at 132 kV, 50 Hz and 0.8 p.f. lagging by means of a transmission line. The series impedance of a single conductor is (20 + j 52) Ω and the total phase-neutral admittance is 315 ×10^-6 mho. Using nominal T method determine, i) The A, B, C and D constants cf the line ii) Sending end voltage.

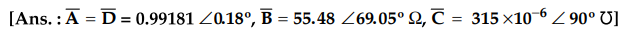
9. A 110 kV, 50 Hz, 3 phase transmission line delivers a load of 40 MW at 0.85 lagging p.f. at the receiving end. The generalised constants of the transmission line are A = D = 0.95 ∠ 1.4°, B = 96 ∠ 78° ohm, C = 0.0015 ∠ 90° mho. Find the regulation of the line and charging current, use nominal T method.  

[Ans.: 30.86%, 106.93] 

10. Find the following for a single circuit transmission line delivering a load of 45 MVA at 352 kV and p.f. 0.8 lagging.

1) Sending end voltage

2) Sending end curent

Given values are A = C = 0.99 ∠ 0.3°; B = ∠ 69° ohms, D = 4.0 ×10^{- 4} ∠  90°, where E_s = AE_r + BI_r and IS = CI_r + DE_r

[Ans.: 87.42 kV, 178.34 A]