Probability and complex function: Unit I: Probability and random variables
Geometric Distribution
Formula, Solved Example Problems | Random variables
Suppose that independent trials, each having a probability p, 0 < p < 1, of being a success, are performed until a success occurs. If we get X equal to the number of trials required, then P{X = x} = (1 − p)x - 1p = qx – 1p , x = 1,2,...
GEOMETRIC
DISTRIBUTION
1. Geometric distribution
Suppose
that independent trials, each having a probability p, 0 < p < 1, of being
a success, are performed until a success occurs. If we get X equal to the
number of trials required, then
P{X
= x} = (1 − p)x - 1p = qx – 1p , x = 1,2,...
Equation
follows because in order for X to equal n, it is necessary and sufficient that
the first x - 1 trials are failures and the nth trial is a success. Equation
then follows, since the outcomes of the successive trials are assumed to be
independent,
Since
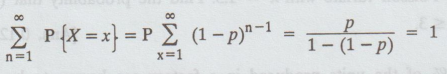
it
follows that with probability 1, a success will eventually occur. Any xod &
de viidedow random variable X whose probability mass function is given by
equation is said to be a geometric random variable with parameter p.
Note:
Geometric distribution has a important application in queueing theory, related
to the number of units which are being served or waiting to be served at any
given time.
2. Recurrence formula for Geometric Distribution.
We
have, P(X = x) = pqx – 1, p + q = 1, x = 1,2,....
P(X
= x + 1) = pqx
So
P (X = x + 1)/ P(X = x) = q
P(X
= x + 1) = q P (X = x)
If
we know P(X = 0 ) then we can write down
P (1), P (2) and so on.
Note 1:
The sum of geometric random variables is negative Binomial, whereas sum of
negative Binomial random variables is negative Binomial.
Note 2: Geometric
distribution has memoryless property that if an event has not occurred during
first r repetitions of an experiment E, then the probability that it will not
occur during the next t repetitions is same as the probability that it will not
occur during the first t repetitions.
Example 1.9.1
If X is a geometric variate taking
values 1, 2, ... ∞, then find P(X is odd). [A.U A/M 2017 R-13]
Solution:
We know that, for a geometric distribution P(X = r)qr - 1p
P(X
is odd) = P(X =1, 3, 5, ...)
=
P(X = 1) + P(X = 3) + P(X = 5) +.....
=
p + q2p + q4p +.....
==
p (1+q2 + q4 + ...)
=
p (1 - q2)-1 = p /(1 + q)(1 - q) = 1/1 + q
Example 1.9.2
If the probability that a target is
destroyed on any one shot is 0.5, what is the probability that it would be
destroyed on 6th attempt? [A.U N/D 2013] [A.U N/D 2017 R-8] [R13 RP]
Solution
:
Given:
p = 0.5; q = 10.5 = 0.5
P(X
= r) = qr - 1 p
P(X
= 6) = q5 p = (1/2)5
½ = 1/26 = 1/64
Example 1.9.3
If the probability is 0.05 that a certain
kind measuring device will show excessive drift, what is the probability that
the sixth of these measuring devices tested will be the first to show excessive
drift?
Solution
: P = 0.05, q = 1- 0.05 = 0.95
P
(X = r) = qr – 1p
P(X
= 6) = (0.95)5 (0.05)
Example 1.9.4.
Suppose that a trainee soldier
shoots a target in an independent fashion. If the probability that the target
is shot on any one shot is 0.8. (i) What is the probability that the target
would be hit on 6th attempt ? (ii) What is the probability that it takes him
less than 5 shots? (iii) What is the probability that it takes him an even
number of shots ? [A.U N/D 2006] [A.U
CBT A/M 2011]
Solution
:
p
= 0.8; q = 1-p = 1 - 0.8 = 0.2
P(X = r) = q r -1. p
(i) The probability that the target would be
hit on the 6th attempt
P(X
= 6) = (0.2)5 (0.8)
(ii)
The probability that it takes him less than 5 shots = P ( X < 5 )
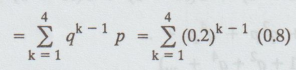
=
(0.8) + (0.2) (0.8) + (0.2)2 (0.8) + (0.2)3 (0.8)
=
0.9984
(iii)
The probability that it takes him an even number of shots is
=
P(X = 2) + P(X = 4) + P(X = 6) + ....
=
(0.2) (0.8) [1 + (0.2)2 + (0.2)4+...]
=(0.2)
(0.8) [1 + (0.04) + (0.04)2 + ....]
=
(0.2) (0.8) [1-0.04] ̄-1
=
(0.2) (0.8) [0.96]-1= 0.1667.
Example 1.9.5.
A and B shoot independently until
each has hit his own target. The probabilities of their hitting the target at
each shot 3/5 and 5/7 respectively. Find the probability that B will require
more shots than A.
Solution:
X → number of trials required by A to get his first success. Then X follows a
geometric distribution given by,
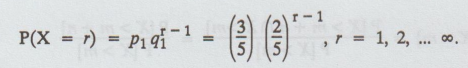 Let
Y→ number of trials required by B to get his first success. Then Y follows a
geometric distribution given by,
Let
Y→ number of trials required by B to get his first success. Then Y follows a
geometric distribution given by,
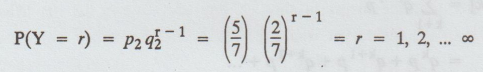
P(B
requires more trials to get his first success than A requires to get his first
success)
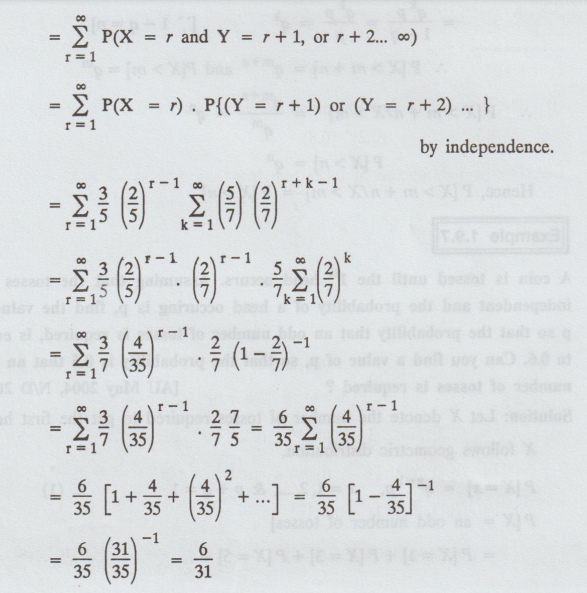
Example 1.9.6
Establish the memoryless property
of geometric distribution. [A.U Trichy A/M 2010] [A.U CH A/M 2011] [A.U N/D
2015 R13 RP] [A.U N/D 2018 R13 RP] [A.U M/J 2006] [A.U N/D 2010]
Sol.
If X has a geometric distribution, then for any two positive integers 'm' and
'n', P[X > m + n /X > m] = p[X >n]
Proof :
P[X
> m + n/ X > m] =

P[X
> m + n / X > m] = qm+ n /qm = qn
P[X
> n] = qn
Hence,
P [X > m + n/ X > m] = P[X > n]
Example 1.9.7
A coin is tossed until the 1st
head occurs. Assuming that the tosses are independent and the probability of a
head occuring is p, find the value of p so that the probability that an odd
number of tosses is required, is equal to 0.6. Can you find a value of p, so
that the probability is 0.5 that an odd number of tosses is required? [AU May
2004, N/D 2010]
Solution:
Let X denote the number of tosses required to get the first head X follows
geometric distribution.
P[X
= x] = qx - 1p, x = 1, 2,
..., & p + q = 1 ....(1)
PIX
= an odd number of tosses]
=
P[X= 1] + P[X = 3] + P[X = 5] + ...
=
p + q2 p + q4 p + ..
=
p[1 + q2 + q4 + ...]
=
P[1- q 2]-1 [ (1-
x)-1 = 1 + x + x2 + ...]
=
p/1 – q2
=
p/(1 + q) (1 - q) = 1/1 + q [p + q = 1]
Given
: P[X = odd number of tosses] = 0.6
⇒ 1/ 1 + q = 0.6 = 3/5
⇒ 1 = (3/5)(1 + q)
⇒ 5/3 – 1 = q
⇒ 2/3 = q
P
= 1 – q = 1 – 2/3 = 1/3
To
find p if P[X = odd number of tosses] = 0.5
(2) ⇒ 1/ 1 + q = 0.5 =
1/2
=>
1 = (1/2)(1 + q)
⇒ 2 = 1 + q
=>
q = 1⇒ p = 0
which
is meaningless. So value of p cannot be found out.
Example 1.9.8
If X1, X2 be
independent random variables each having geometric distribution qKp,
K = 0, 1, 2, Show that the conditional distribution of X1 given X1+
X2 is uniform. [A.U N/D 2006]
Solution:
Given: P(X1 = K) = P(X2 = K) = pqK, K =
0,1,2,...
(i.e.,)
P(X1 = K) = P(X2 = K) = pqK - 1, K = 1, 2, ...
X1+
X2 = n is a discrete uniform distribution.
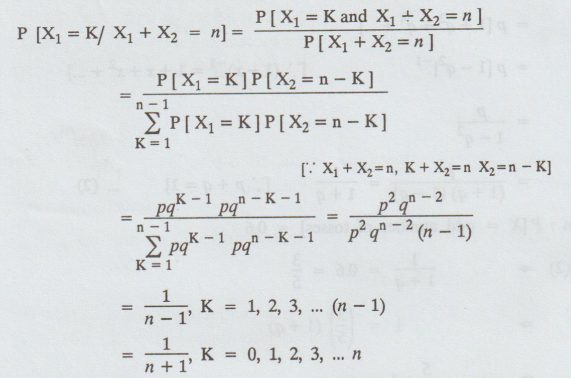
Note:
When P[X =r] = constant, the discrete random variable X is said to follow a
discrete uniform distribution.
Thus
the conditional distribution of X, given that X + Y = n, is a discrete uniform
distribution.
Example 1.9.9
If the probability that an
applicant for a driver's licence will pass the road test on any given trial is
0.8, what is the probability that he will finally pass the test (a) on the
fourth trial and (b) in fewer than 4 trials ? [A.U Trichy A/M 2010] [A.U A/M
2010, N/D 2012] [A.U A/M 2015 (RP) R13] [A.U A/M 2017 R-08]
Solution:
Let X denote the number of trials required to achieve the first success. Then X
is a geometric distribution given by
P
(X = r) = qr - 1p; r = 1, 2, 3, ..., ∞
Here
p = 0.8 and q = 0.2
(a)
P (X = 4) =(0.2)4 - 1 (0.8) (0.2)3 (0.8) = 0.0064
(b)
P (X < 4) = P[X = 1] + P(X = 2] + P [X = 3]
=
(0.2)1 - 10.8+ (0.2)2 - 1 (0.8) + (0.2)3 - 1
(0.8)
=
[1 +0.2 + (0.2)2] (0.8) = 0.992
Probability and complex function: Unit I: Probability and random variables : Tag: : Formula, Solved Example Problems | Random variables - Geometric Distribution
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
