Gradient of a Scalar

Gradient of a Scalar

AU: May-04,08,10,12, Dec.-04,10,13,18

• Consider that in space let W be the unique function of x, y and z co-ordinates in the cartesian system. This is the scalar function and denoted as W (x, y, z). Consider the vector operator in cartesian system denoted as  called del. It is defined as,

Key Point : The operation of the vector operator del () on a scalar function is called gradient of a scalar.

Key Point : Gradient of a scalar is a vector.

• The gradient of a scalar W in various co-ordinate systems are given by,

1 .Properties of Gradient of a Scalar

The various properties of a gradient of a scalar field W are,

• 1. The gradient W gives the maximum rate of change of W per unit distance.

• 2. The gradient  W always indicates the direction of the maximum rate of change of W.

• 3. The gradient  W at any point is perpendicular to the constant W surface, which passes through the point.

• 4. The directional derivative of W along the unit vector a is (dot product), which is projection of  W in the direction of unit vector 

• If U is the another scalar function then,

Ex 1.17.1 Find the gradient of scalar system t = x²y + e^z at point P(1,5,-2) AU: May-08, Marks 8

Sol. :

t = x²y + e^z  and P(1,5,-2)

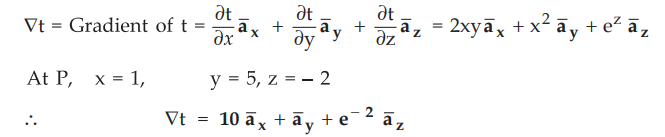
Ex. 1.17.2 Find the gradient of the following scalar fields :  1) V = e^-z sin 2x cosh y 2) U = p²z cos2ϕ 3) W = 10r sin²θ cos ϕ AU:May-10, Marks 2+2+2

Sol. : 1) V = e^-z sin 2x cosh y

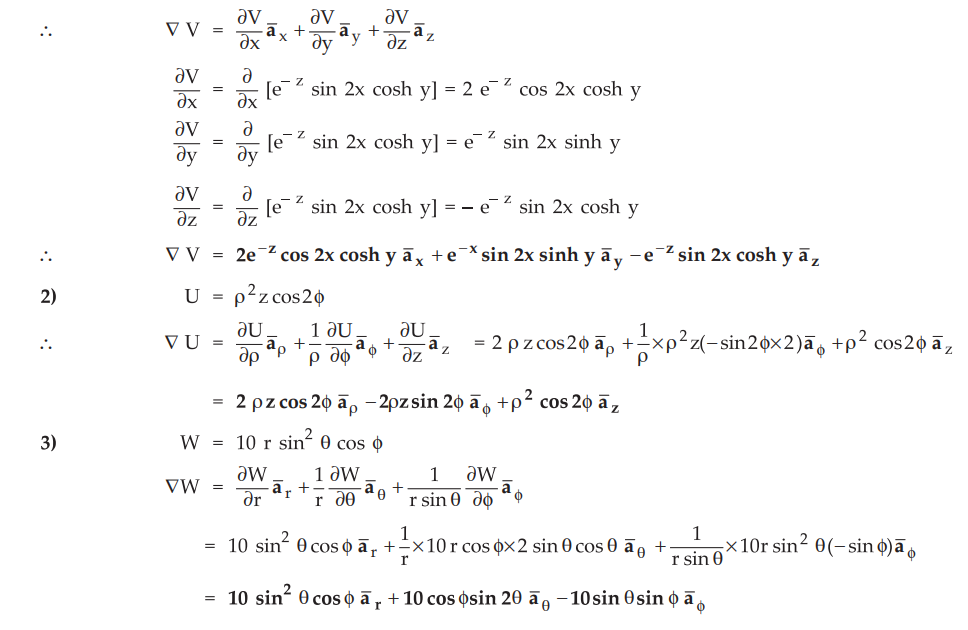
Ex. 1.17.3 Obtain in the spherical co-ordinate system the gradient of the function f(r, θ, ϕ) = 25r⁴sin θ cos ϕ+ 2cos θ + 5rsin ϕ AU: May-12, Marks 8

Sol. : Gradient of f in spherical system is,

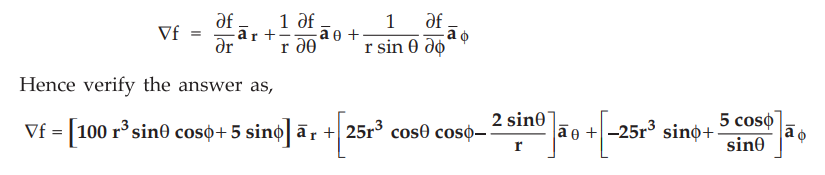
Examples for Practice

Ex. 1.17.4 The temperature in an auditorium is given by, T = x² + y²- z. A mosquito at (1, 1, 2) in the auditorium desires to fly in such a direction that it will get warm as soon as possible. In what direction must it fly?

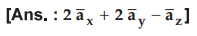
Ex. 1.17.5 If U = xz - x²y + y2z² evaluate div grad U.

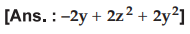
Ex. 1.17.6 Obtain in the spherical co-ordinate system the gradient of the function f(r, θ, ϕ )  = 25r⁴ sin θ cos ϕ + 2cos θ + 5r sin ϕ AU: May-12, Marks 8 

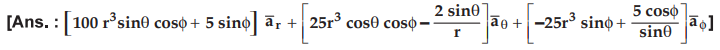
Review Questions

1. Write a note on gradient. AU: May-04, Dec.-04, 10, 13, Marks 4

2. Write the expression for gradient in three co-ordinate systems. AU: Dec.-18, Marks 3