Grading of Cables

Grading of Cables

We have seen that the stress in the insulation is maximum at the conductor surface and minimum at the sheath. To avoid the breakdown of the insulation, it is necessary to have uniform distribution of stress all along the insulation.

Practically some methods are used to obtain uniform distribution of stress. The process of obtaining uniform distribution of stress in the insulation of cables is called grading of cables.

The unequal distribution of stress has two effects,

1. Greater insulation thickness is required, which increases the cost and size.

2. It may lead to the breakdown of insulation.

Hence the grading of cables is done.

There are two methods of grading the cables which are,

1. Use of intersheaths for grading

2. Capacitance grading

Let us discuss these two grading methods in detail.

 

1. Use of Intersheaths for Grading

In this method of grading, in between the core and the lead sheath number of metallic sheaths are placed which are called intersheaths. All these intersheaths are maintained at different potentials by connecting them to the tappings of the transformer secondary. These potentials are between the core potential and earth potential. Generally lead is used for these sheaths as it is flexible and corrosion resistance but as its mechanical strength is less, aluminium also can be used. Aluminium is low weight and mechanically strong but it is much costlier than lead. 

Using the intersheaths, maintaining at different potential, uniform distribution of stress is obtained in the cables.

Consider a cable with core diameter d and overall diameter with lead sheath as D. Let two intersheaths are used having diameter d₁ and d₂ which are kept at the potentials V₁ and V₂ respectively.

The intersheaths and stress distribution is shown in the Fig. 6.8.1.

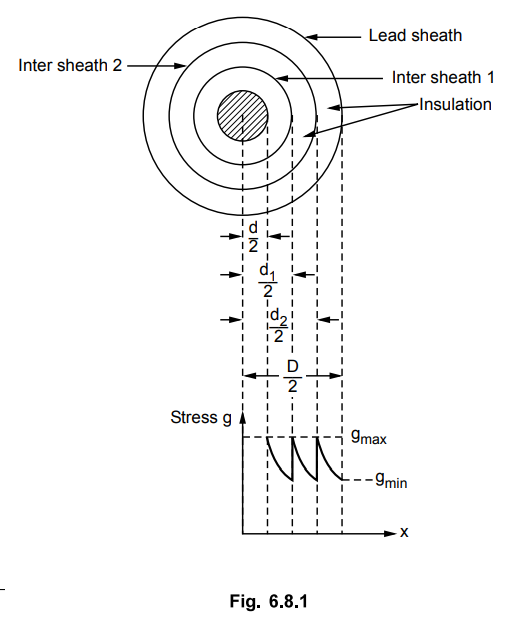
Let V₁ = Voltage of intersheath 1 with respect to earth

V₂ = Voltage of intersheath 2 with respect to earth

It has been proved that stress at a point which is at a distance x is inversely proportional to distance x and given by,

g_x = Q / 2π εx = k / x  ... (6.8.1)

where k is constant.

So electric stress g₁ between the conductor and intersheath 1 is,

g₁ = k₁ / x where k₁ = Constant

Now potential difference between core and the first intersheath is V – V₁. 

The potential difference between intersheath 2 and outermost sheath is V₂ only as potential of intersheath is maintained at V₂ with respect to earth.

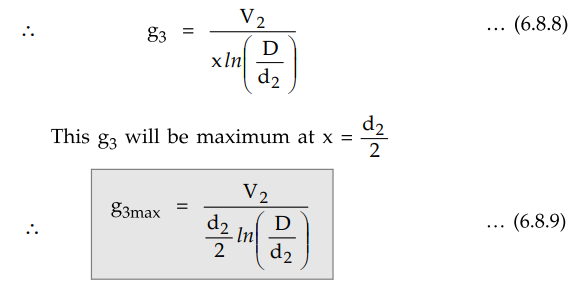
Choosing proper values of V₁ and V₂, g_lmax, g_2max etc. can made equal and hence uniform distribution of stress can be obtained.

The stress can be made to vary between same maximum and minimum values as shown in the Fig. 6.6.1, by choosing d₁ and d₂ such that,

Example 6.8.1 A single core cable of conductor diameter 2 cm and lead sheath of diameter 5.3          cm is to be used on a 66 kV, 3-phase system. Two inter sheaths of diameter 3.1 cm and 4.2 cm are introduced between the core and lead sheath. If the maximum stress in the layers is the same, find the voltages on the inter sheath.

Solution : d = 2 cm, D = 5.3 cm, V_line = 66 kV,

Solving equations (4) and (5), V1 = 36.988 kV, V2 = 18.8373 kV.

 

Example 6.8.2 A single core cable has a conductor of diameter 2.5 cm and a sheath of inside diameter 6 cm. Calculate the maximum stress. It is desired of reduce the maximum stress by using two intersheaths. Determine their best positions, the maximum stress and the voltages on each system. Voltage is 66 kV, 3 phase.

Solution :   d = 2.5 cm and D = 6 cm, V_line = 66 kV

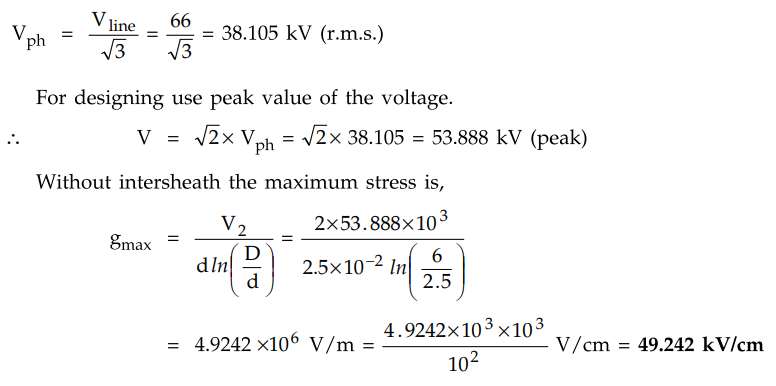
Now two intersheaths are to be used. Let d1 and d2 be the diameters of the two sheaths and maintained at the voltage Vx and V2 respectively. The best position is such that the stress in all the sections vary between the same maximum and minimum values which is possible when,

 

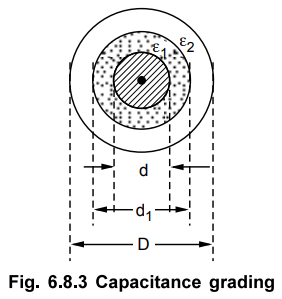
2. Capacitance Grading

The grading done by using the layers of dielectrics having different permittivities between the core and the sheath is called capacitance grading.

In intersheath grading, the permittivity of dielectric is same everywhere and the dielectric is said to be homogeneous. But in case of capacitance grading, a composite dielectric is used.

Let d₁= Diameter of the dielectric with permittivity ε₁

and D = Diameter of the dielectric with permittivity ε₂ This is shown in the Fig. 6.8.3.

The stress at a point which is at a distance x is inversely proportional to the distance x and given by,

g_x = Q / 2π εx

Hence the stress at any point in the inner dielectric is,

g₁ = Q / 2π ε₁x

Similarly the dielectric stress in the outer dielectric is,

g₂ = Q / 2π ε₂x

Hence the total voltage V can be expressed as,

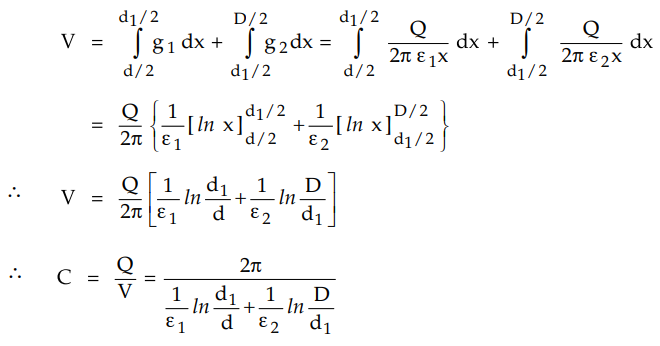
The stress is maximum at surface of conductor i.e. x = d/2.

Key Point Thus the electric stress is inversely proportional to the permittivities and the inner radii of the dielectrics.

a. Condition for Equal Maximum Stress

Let us obtain the condition under which the maximum values of the stresses in the two regions are equal.

The maximum stresses are given by,

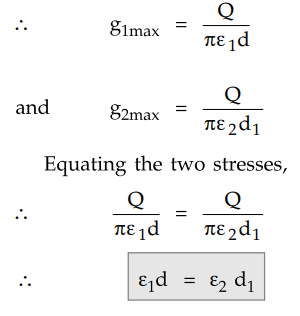
Now d₁ is greater than d so to satisfy above equation ε₂ must be less than ε1.

Thus the dielectric nearest to the conductor must have the highest permittivity.

Similar for the grading with three dielectrics with permittivities ε₁ , ε₂ and ε₃, for equal maximum stress the condition is,

 

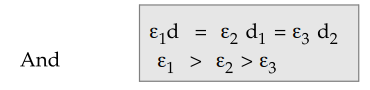
3. Difficulties in Grading

In the intersheath grading, the intersheath has to be thin. Hence there is possibility of damage to it while laying the cable. Similarly intersheath has to carry the charging current which can cause overheating of cable.

In capacitance grading, to have uniform distribution of stress it is necessary to select the dielectrics of proper permittivities. But practically it is difficult to get the proper values of permittivities. Similarly the permittivity of dielectric changes with the time which can cause uneven distribution of stress. Such uneven distribution may lead to breakdown at the normal operating voltage.

 

Example 6.8.3 For the same conductor diameter and overall dimensions compare the maximum permissible potential difference between the core and sheath when the cable is :

1. Ungraded with homogeneous dielectric

2. Graded with 3 dielectrics with permittivities 5, 4 and 3.

The maximum permissible potential gradient for all the dielectrics is the same and equals 33 kV/cm. The core diameter is 2 cm and the sheath diameter is 6 cm.

Solution : Case 1 : Ungraded cable

 

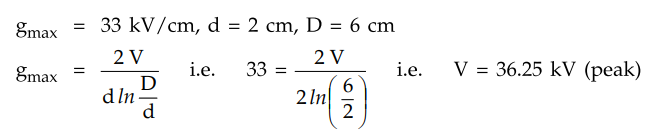
Permissible r.m.s. voltage for the cable is,

Key Point Thus the graded cable can withstand 1.42 times more voltage than the ungraded cable.

 

Example 6.8.4 A single core 66 kV cable has a conductor diameter of 2 cm and a sheath of inside diameter 5.3 cm. The cable has an inner layer of 1 cm thickness of rubber with dielectric constant 4.5 and the rest is impregnated paper with dielectric constant 3.6. Find the maximum stress in each dielectric.

Solution :  

d = 2 cm, D = 5.3 cm, t₁ = 1 cm, ε₁ = 4.5, ε₂ = 3.6

 

Example 6.8.5 Find the radius of the intersheath and the potential at which it must be maintained for a single core metal sheathed cable such that the overall radius of the cable is minimum. The operating voltage is V and overall diameter is D then show that, D = 3.76V / g_max , is the maximum stress in dielectric

Solution : Let d = Diameter of conductor, D = Overall diameter of cable

d₁ = Diameter of intersheath, V₁ = Potential of intersheath

To have overall diameter D minimum, conductor size d and also must be minimum for which we can write the relation as,

d₁ = 2.718 d         ... (1)

This is due to intersheath in between.

Now the maximum stress in between conductor and intersheath occurs on surface of the conductor given by,

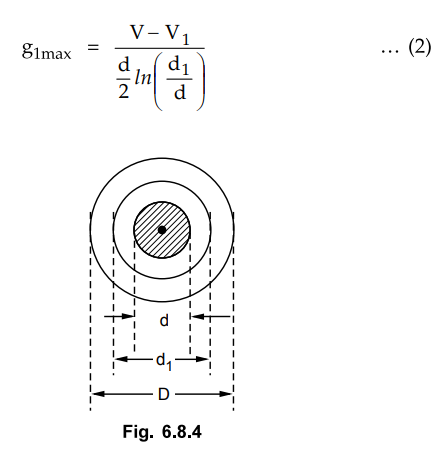
While the potential of intersheath is V₁ and lead outer sheath is earthed so maximum stress between intersheath and outermost sheath occurs on surface of intersheath given by,

And the minimum overall diameter can be obtained by substituting equations (11) and (12) in equation (9).

 

 

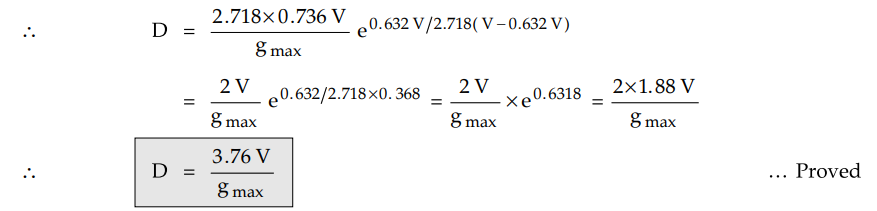
Example 6.8.6 A single core metal sheathed cable operating on 66 kV, 1 phase system is to be graded by a metallic intersheath. The core diameter is 2 cm and insulating material has a permissible potential gradient of 60 kV/cm. Find :

a) The diameter of the intersheath

b) The potential at which intersheath must be maintained

c) The diameter of outer sheath.

Calculate the sheath diameter if cable is not graded under same core diameter and operating conditions.

Solution : d = 2 cm, V = 66 kV (r.m.s.), g_max = 60 kV/cm

The arrangement is shown in the Fig. 6.8.5.

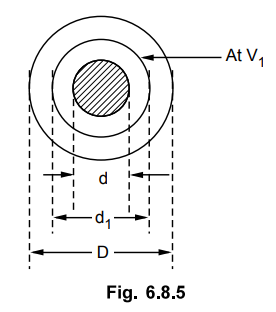
The maximum stress in between core and intersheath is given by,

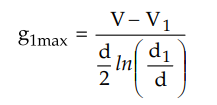
While the maximum stress between intersheath and outer sheath is given by,

To vary the stress between same maximum and minimum values,

d₁/ d = D / d₁ = α

d₁ = d α and D = d₁  α = dα² and d = 2

Substituting in equations (1) and (2),

 

Example 6.8.7 A single core cable of conductor diameter 2 cm and lead sheath of diameter 5.3 cm is to be used on a 66 kV, 3 systems. Two inter sheath of diameter 3.1 cm and 4.2 cm are introduced between the core and lead sheath. If the maximum stress in the layers is the same, find the voltage on the inter sheaths.

Solution :   d = 2 cm, D = 5.3 cm, d₁ = 3.1 cm, d₂ = 4.2 cm, V_line = 66 kV

Solving equations (1) and (2), V₁ = 36.988 kV, V₂ = 18.837 kV

 

Example 6.8.8 A conductor of 1 cm diameter passes centrally through a porcelain cylinder of internal diameter 2 cms and external diameter 7 cms. The cylinder is surrounded by a tightly fitting metal sheath. The permitivity of porcelain is 5 and the peak voltage gradient in air must not exceed 34 kV/cm. Determine the maximum safe working voltage.

AU : Dec.-04, Marks 8

Solution : For the given cable, d = 1 cm, d₁ = 2 cm, and D = 7 cm

Thus dielectric 1 is air with = ε₀ while the dielectric 2 is porcelain with ε₂  = ε₀ ε_r = 5 ε₀

 

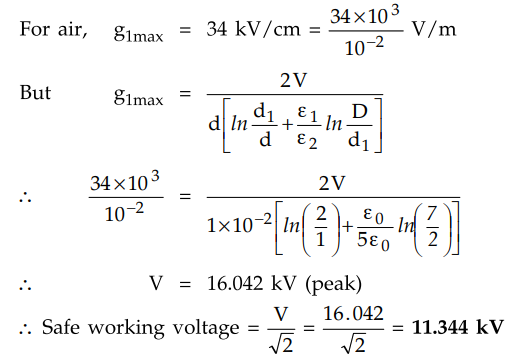
Example 6.8.9 Prove that the ratio of voltage gradient with and without intersheath will be 2/ (1+α) when there is only one layer of intersheath. (Ratio of intersheath radius to core radius = (Outer sheath to intersheath radius = α)

AU: May-06, Marks 8

Solution:  The intersheath is shown in the Fig. 6.8.6.

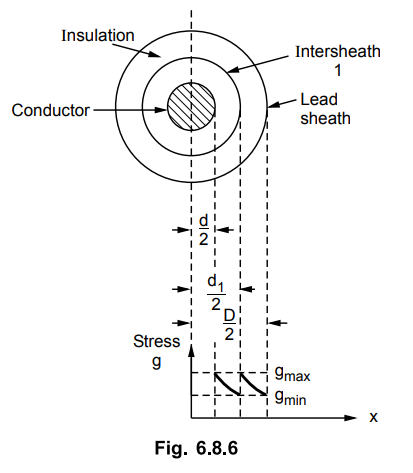
Let V₁ = Voltage of intersheath 1 with respect to earth.

The stress at a point which is at a distance x is inversely proportional to x and given by,

g_x = Q / 2 πε x = k / x

So electric stress between conductor and intersheath 1 is,

g₁ = k₁ / x

where k₁ = Constant

The potential difference between core and intersheath 1 is V - V₁

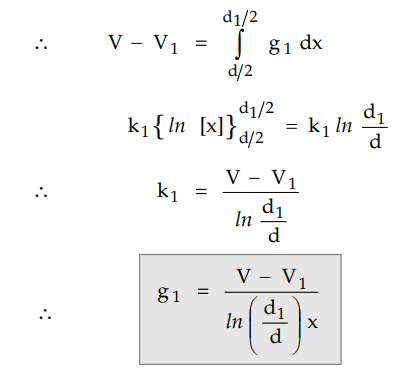
The potential difference between intersheath 1 and outermost sheath is V₁ only as outer sheath is at earth.

The ratio of voltage gradient with and without intersheath is,

 

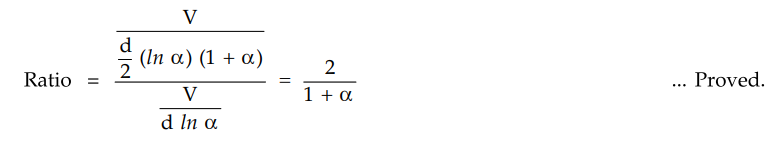
Example 6.8.10 A single core, lead covered cable is to be designed for 66 kV to earth. Its conductor radius is 0.5 cm and its three insulating materials A, B and C have the relative permittivities of 4, 4 and 2.5 with maximum permissible stresses of 50, 40 and 30 kV/cm respectively. Find the minimum internal diameter of the lead sheath.

AU : Dec.-06, Marks 10

Solution : r = 0.5 cm hence d = 2 × r = 1 cm

 

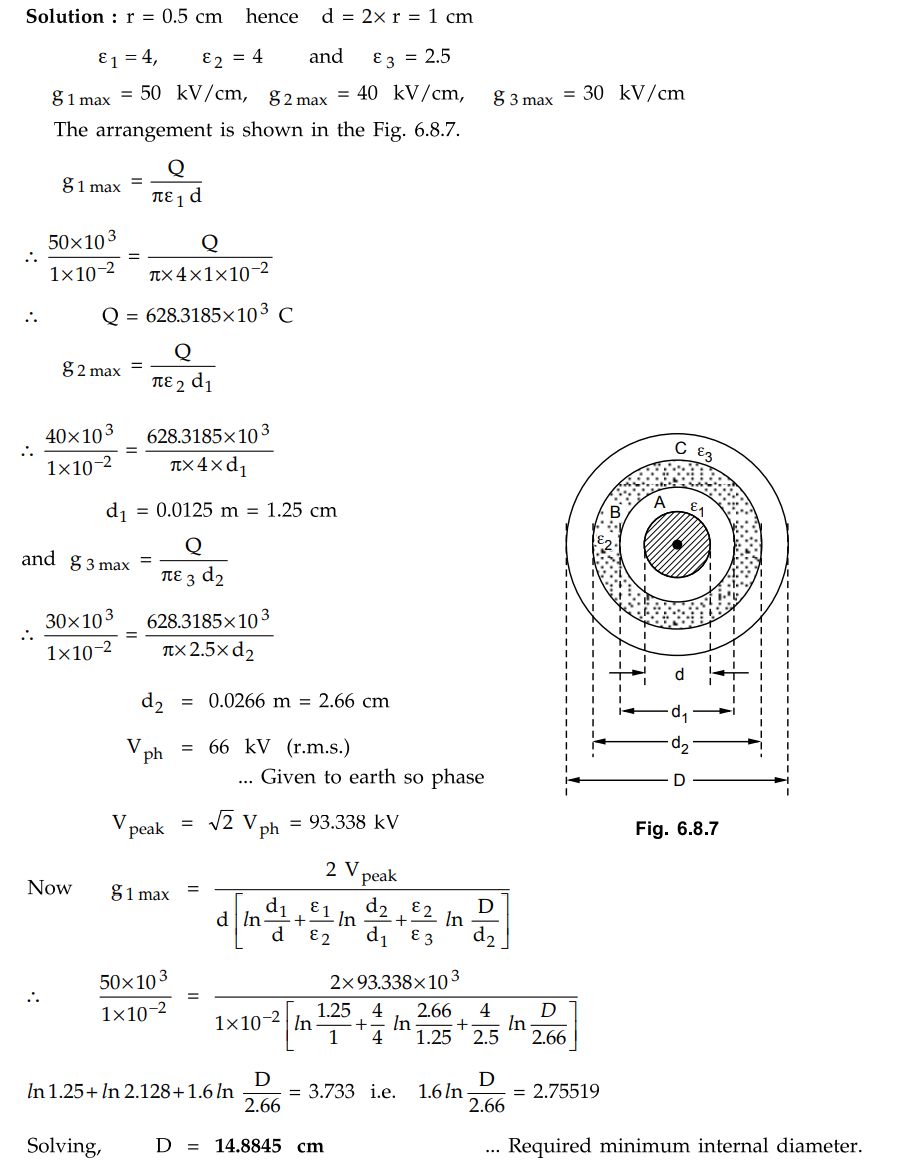
Example 6.8.11 A 66 kV, single core metal sheathed cable is to be graded by means of a metallic intersheath. Calculate the diameter of the intersheath and the voltage at which it must be maintained in order to obtain minimum overall diameter. The maximum voltage gradient at which the insulating material can be worked is 60 kV/cm. Derive the formula used.

Solution : For the derivation of formula, refer example 6.8.5. From the results,

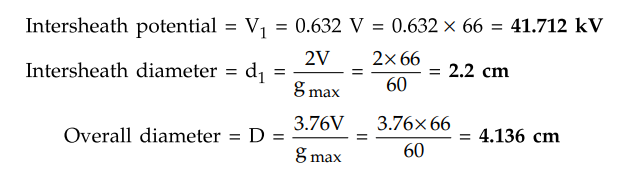
Review Questions

1. What is grading of cables ? Discuss the capacitance grading of cables in detail.

2. Discuss the intersheath grading of cables in detail.

3. With neat diagram, explain the various methods of grading of underground cables.

4. A single core lead sheathed cable is graded using two dielectrics of relative permittivity 3.6 (inner) and 2.5(outer), the thickness of each being 1 cm. The core diameter is 1 cm. System voltage is 66 kV (line value), 3 phase. Determine the maximum stress in the two dielectrics.

[Ans.: 29.376 kV/cm (peak), 28.20 kV/cm]

5. A 66 kV single cores lead sheathed cable is graded by using two dielectrics of relative permittivity 5 and 3 respectively, thickness of each being 1 cm. The core diameter is 2 cm. Determine the maximum stress in the two dielectrics.

[Ans.: 39.36 kV/cm, 32.81 kV/cm]

6. Show that in a cable using two intersheaths the maximum stress in the dielectric reduces by the factor 1 / (1/3) (1 + a + a²) of the maximum stress in an ungraded cable where d₁ / d = d₂ / d₁ = D / d₂ = a

and D = Sheath diameter, d = Core diameter whiled₁  and d₂ are the diameters of intersheaths.

7. A cable has intersheath grading which satisfies d₁ / d = D / d₁ = a

The conductor diameter is 2 cm while the intersheath diameter is 5 cm. Determine the location of the intersheath. Calculate the ratio cf maximum electric stress with and without intersheath.

[Ans.: Intersheath diameter 8.16 cm, 0.775]

8. A single core cable is graded using two dielectrics of relative permittivities 3.6 and 2.5 and thickness of each is 1 cm. The conductor diameter is 1 cm. The system voltage is 66 kV, 3 phase. Determine the peak values cf the maximum stress in the two dielectrics.

[Ans.: 58.76 kV/cm, 28.21 kV/cm]