Half Wave Rectifier

Half Wave Rectifier

AU : May-11,12, Dec.-15, 16

• In half wave rectifier, rectifying element conducts only during positive half cycle of input a.c. supply. The negative half cycles of a.c. supply are eliminated from the output.

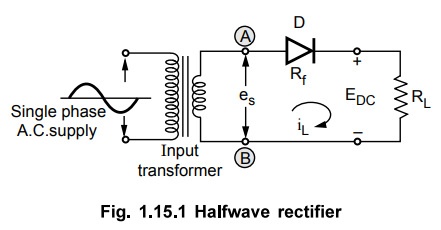
• This rectifier circuit consists of resistive load, rectifying element, i.e. p-n junction diode, and the source of a.c. voltage, all connected in series. The circuit diagram is shown in the Fig. 1.15.1. Usually, the rectifier circuits are operated from a.c. mains supply. To obtain the desired d.c. voltage across the load, the a.c. voltage is applied to rectifier circuit using suitable step-up or step-down transformer, mostly a step-down one, with necessary turns ratio.

• The input voltage to the half-wave rectifier circuit shown in the Fig. 1.15.1 is a sinusoidal a.c. voltage, having a frequency which is the supply frequency, 50 Hz.

• The transformer decides the peak value of the secondary voltage. If Nj are the primary number of turns and N2 are the secondary number of turns and Epm is the peak value of the primary voltage then,

N₂ / N₁ = E_am / E_pm

• Where E_pm = The peak value of the secondary a.c. voltage. 

• As the nature of is sinusoidal the instantaneous value will be,

es = E_sm sin ωt

where          ω = 2π f and f = Supply frequency

• Let R_f represents the forward resistance of the diode. Assume that, under reverse biased condition, the diode acts almost as an open circuit, conducting no current.

 

1. Operation of the Circuit

• During the positive half cycle of secondary a.c voltage, terminal (A) becomes positive with respect to terminal (B). The diode is forward biased and the current flows in the circuit in the clockwise direction, as shown in the Fig. 1.15.2 (a). The current will flow for almost full positive half cycle. This current is also flowing through load resistance R_L hence denoted as i_L, the load current.

• During negative half cycle when terminal (A) is negative with respect to terminal (B), diode becomes reverse biased. Hence no current flows in the circuit as shown in the Fig. 1.15.2 (b). Thus the circuit current, which is also the load current, is in the form of half sinusoidal pulses.

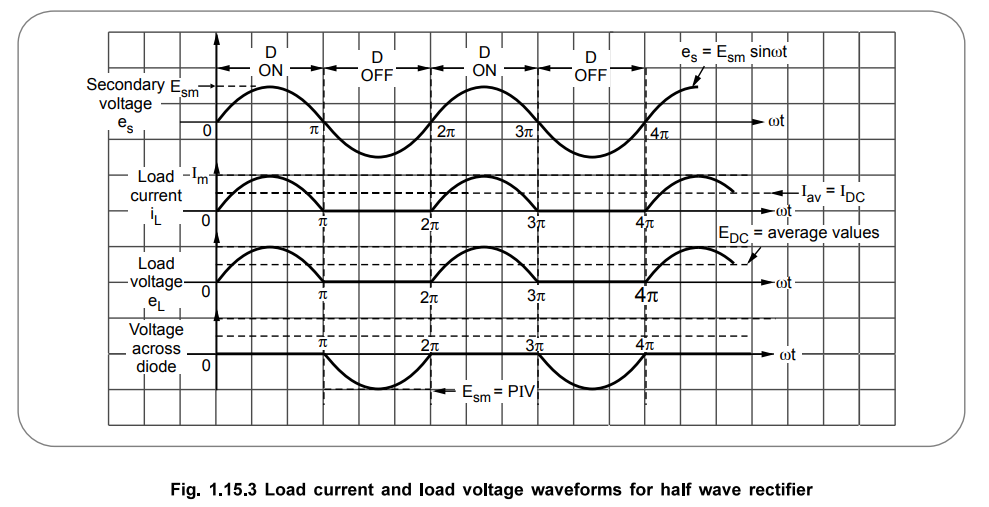
• The load voltage, being the product of load current and load resistance, will also be in the form of half sinusoidal pulses. The different waveforms are illustrated in Fig. 1.15.3.

• The d.c. output waveform is expected to be a straight line but the half wave rectifier gives output in the form of positive sinusoidal pulses.

Key Point : Hence the output is called pulsating d.c. It is discontinuous in nature. Hence it is necessary to calculate the average value of load current and average value of output voltage.

 

2. Average D.C. Load Current (lDC)

• The average or d.c. value of alternating current is obtained by integration.

• For finding out the average value of an alternating waveform, we have to determine the area under the curve over one complete cycle i.e. from 0 to 2n and then dividing it by the base i.e. 2π .

• Mathematically, current waveform can be described as,

i_L = I_m sin ωt     for 0 ≤ ωt ≤  π

i_L = 0                for π ≤ ωt ≤ 2π

where          I_m = Peak value of load current

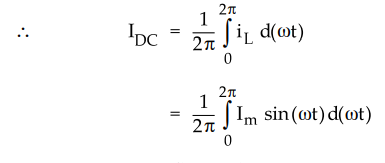
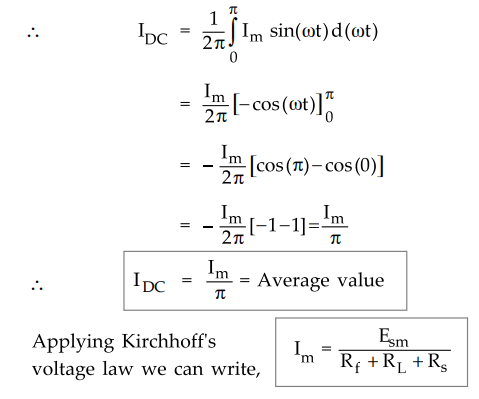
• As no current flows during negative half cycle of a.c. input voltage, i.e. between ωt = π to ωt = 2 π, we change the limits of integration.

• where R_S = Resistance of secondary winding of transformer. If R_S is not given it should be neglected while calculating I_m .

 

3. Average D.C. Load Voltage (E_DC)

• It is the product of average D.C. load current and the load resistance R_L.

E_DC = I_DCR_L

• Substituting value of I_DC,

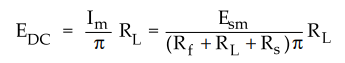
• The winding resistance Rs and forward diode resistance Rf are practically very small compared to R_L

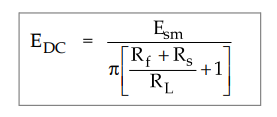
• But as Rf and Rg are small compared to RL , (Rf + RS)/RL is negligibly small compared to 1. So neglecting it we get,

EDC ≈ Esm / π

Note : When Rf and Rg are finite, calculate Im, then IDC and from that calculate E_DC as I_DCR_L

Key Point : Do not calculate E_DC as Esm / π directly for finite R, and R . Calculate I_m then I_DC and then E_DC as I_DCR_L

 

4. R.M.S. Value of Load Current (I_RMS)

The R.M.S means squaring, finding mean and then finding square root. Hence R.M.S. value of load current can be obtained as,

Note : Students must remember that this R.M.S. value is for half wave rectified waveform hence it is I_m/2. For full sine wave it is I_m/√2        which is derived later.

 

5. D.C. Power Output (PDC)

The d.c. power output can be obtained as,

 

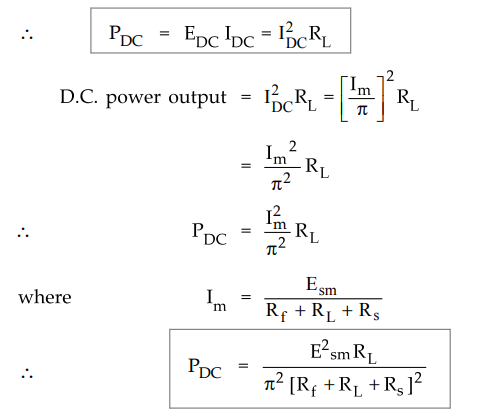
6. A.C. Power Input (P_AC)

The power input taken from the secondary of transformer is the power supplied to three resistances namely load resistance R_L , the diode resistance Rf and winding resistance R_S. The a.c. power is given by,

 

7. Rectifier Efficiency

• The rectifier efficiency is defined as the ratio of output d.c. power to input a.c. power.

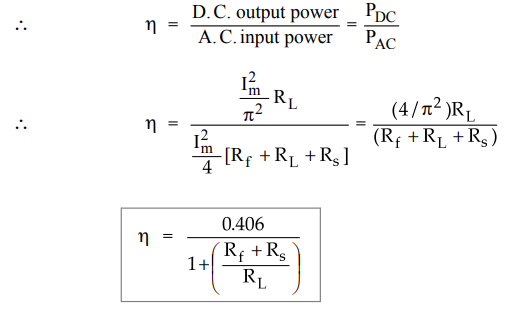
• If (Rf + Rs) << R_L as mentioned earlier, we get the maximum theoretical efficiency of half wave rectifier as,

% η_max = 0.406 × l0° = 40.6 %

• Thus in half wave rectifier, maximum 40.6 % a.c. power gets converted to d.c. power in the load. If the efficiency of rectifier is 40 % then what happens to the remaining 60 % power. It is present interms of ripples in the output which is fluctuating component present in the output.

Key Point : Thus more the rectifier efficiency, less are the ripple contents in the output.

 

8. Ripple Factor (ɤ)

• It is seen that the output of half wave rectifier is not pure d.c. but a pulsating d.c. The output contains pulsating components called ripples. Ideally there should not be any ripples in the rectifier output. The measure of such ripples present in the output is with the help of a factor called ripple factor denoted by ɤ It tells how smooth is the output.

Key Point : Smaller the ripple factor closer is the output to a pure d.c.

• The ripple factor expresses how much successful the circuit is, in obtaining pure d.c. from a.c. input.

Definition :

• Mathematically ripple factor is defined as the ratio of R.M.S. value of the a.c. component in the output to the average or d.c. component present in the output.

Ripple factor

ɤ  = R.M.S. value of a.c. component of output / Average or d.c. component of output

• Now the output current is composed of a.c. component as well as d.c. component.

Let     I_ac = R.M.S. value of a.c. component present in output

I_DC = D.C. component present in output

• This is the general expression for ripple factor and can be used for any rectifier circuit.

• Now for a half wave circuit,

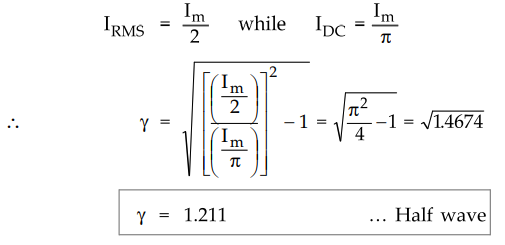
• This indicates that the ripple contents in the output are 1.211 times the d.c. component i.e. 121.1 % of d.c. component.

Key Point : The ripple factor for half wave is very high which indicates that the half wave circuit is a poor converter of a.c. to d.c.

• The ripple factor is minimised using filter circuits along with the rectifiers.

 

9. Load Current

• The load current i_L which is composed of a.c. and d.c. components can be expressed using Fourier series as,

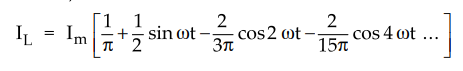
• This expression shows that the current may be considered to be the sum of an infinite number of current components, according to Fourier series.

• The first term of the series is the average or d.c. value of the load current. The second term is a varying component having frequency same as that of a.c. supply voltage. This is called fundamental component of the current having frequency same as the supply. The third term is again a varying component having frequency twice the frequency of supply voltage. This is called second harmonic component. Similarly all the other terms represent the a.c. components and are called harmonics.

• Thus ripple in the output is due to the fundamental component along with the various harmonic components. And the average value of the total pulsating d.c. is the d.c. value of the load current, given by the constant term in the series, I_m / π.

 

10. Peak Inverse Voltage (PIV)

• The Peak Inverse Voltage is the peak voltage across the diode in the reverse direction i.e. when the diode is reverse biased. In half wave rectifier, the load current is ideally zero when the diode is reverse biased and hence the maximum value of the voltage that can exist across the diode is nothing but Egm. This is shown in the Fig. 1.15.4.

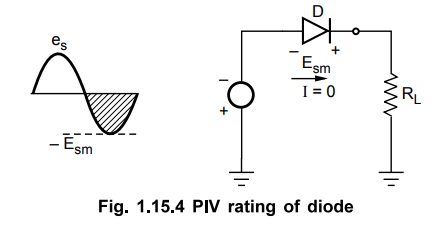
• Thus PIV occurs at the peak of each negative half cycle of the input, when diode is reverse biased and not conducting.

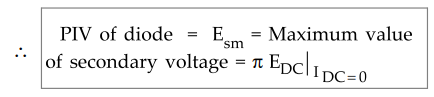
• This is called PIV rating of a diode. So diode must be selected based on this PIV rating and the circuit specifications.

 

11. Transformer Utilization Factor (T.U.F.)

• The factor which indicates how much is the utilization of the transformer in the circuit is called Transformer Utilization Factor (T.U.F.)

Definition :

• The T.U.F. is defined as the ratio of d.c. power delivered to the load to the a.c power rating of the transformer. While calculating the a.c. power rating, it is necessary to consider r.m.s. value of a.c. voltage and current.

• The T.U.F. for half wave rectifier can be obtained as,

A.C. power rating of transformer =

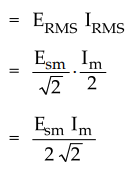
• Remember that the secondary voltage is purely sinusoidal hence its r.m.s. value is 1/V2 times maximum while the current is half sinusoidal hence its r.m.s. value is 1/2 of the maximum, as derived earlier.

D.C. power delivered to the load =

Key Point : The value of T.U.F. is low which shows that in half wave circuit, the transformer is not fully utilized.

 

12. Voltage Regulation

• The secondary voltage should not change with respect to the load current. The voltage regulation is the factor which tells us about the change in the d.c. output voltage as load changes from no load to full load condition.

Key Point : Less the value of voltage regulation, better is the performance of rectifier circuit.

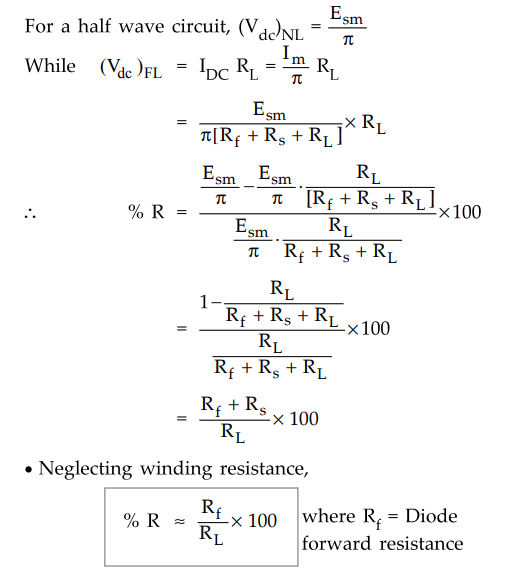
Key Point : Ideally the load regulation is zero as ideal value of R_f is zero in forward biased condition.

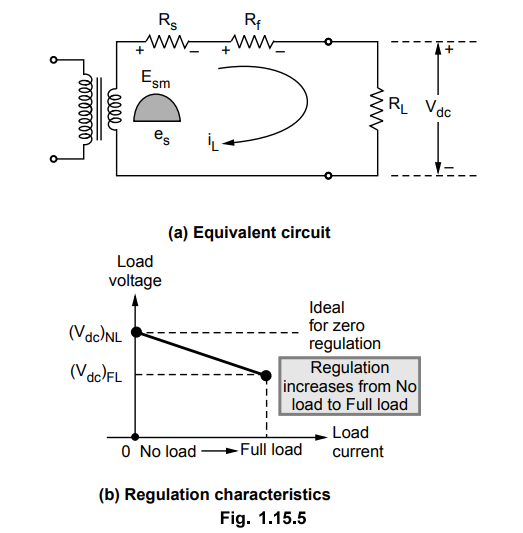
a. Regulation Characteristics

• Consider the equivalent circuit of the half wave rectifier, for positive half cycle of the transformer secondary voltage as shown in the Fig. 1.15.5 (a).

• As load current increases (RL decreases), the drop across Rg and Rf goes on increasing, but the transformer, secondary voltage remains same. Hence the d.c. output voltage decreases. Hence load voltage decreases as load changes from no load to full load. To keep the drop across Rg and Rf minimum, values of Rg and Rf. must be as small as possible. The graph of load voltage against load current is called regulation characteristics which is drooping in nature as shown in the Fig. 1.15.5 (b). 

 

13. Advantages of Half Wave Rectifier

1. Only one diode is sufficient.

2. Easy to design.

3. Centre tap transformer is not required.

 

14. Disadvantages of Half Wave Rectifier Circuit

• The various disadvantages of the half wave rectifier circuit are,

1. The ripple factor of half wave rectifier circuit is 1.21, which is quite high. The output contains lot of varying components.

2. The maximum theoretical rectification efficiency is found to be 40 %. The practical value will be less than this. This indicates that half wave rectifier circuit is quite inefficient.

3. The circuit has low transformer utilization factor, showing that the transformer is not fully utilized.

4. The d.c. current is flowing through the secondary winding of the transformer which may cause dc saturation of the core of the transformer. To   minimize the saturation, transformer size have to be increased accordingly. This increases the cost.

• Because of all these disadvantages, the half-wave rectifier circuit is normally not used as a power rectifier circuit.

• Due to the barrier potential of 0.7 V for Si diode, the peak value of the output is 0.7 V less than peak value of the input voltage.

V_P (output) = E_sm - 0.7V

• This effect is generally neglected as peak value of the input voltage is much greater than the barrier potential of 0.7 V. For Ge diodes, barrier potential is about 0.2 V which is very small and practically neglected.

 

Ex. 1.15.1 A half wave rectifier circuit is supplied from a 230 V, 50 Hz supply with a step down ratio of 3 : 1 to a resistive load of 10 fcQ. The diode forward resistance is 75 Q while transformer secondary resistance is 10 Q. Calculate maximum, average, RMS values of current, D.C. output voltage, efficiency of rectification, regulation and ripple factor.

Sol. : The circuit is shown in the Fig. 1.15.6.

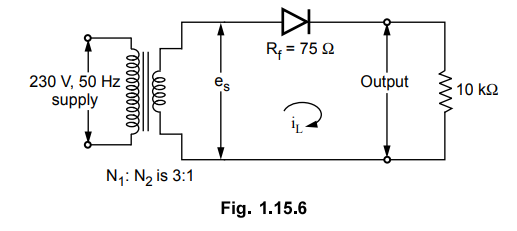
• The given values are,

R_f = 75 Ω, R_L = 10 k Ω, Rs = 10 Ω.

• The given supply voltages are always r.m.s. values.

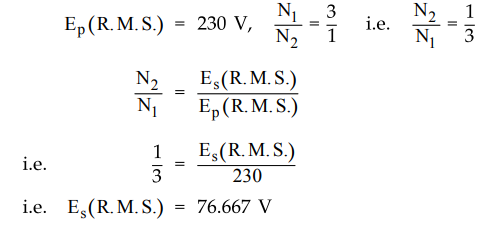
• This is r.m.s. value of the transformer secondary voltage.

Review Questions

1. What is half wave rectifier ? Explain the working principle with neat sketch.

AU : May-11, Dec.-15, 16, Marks 8

2. Derive the expressions for the following parameters of the half wave rectifier circuit :

a. Average d.c. current (I_DC)

b. Average d.c. voltage (E_DC)

c. R.M.S. value of current (I_RMS)

d. D.C. power output (P_DC)

e. A.C. power input (P_AC)

f. Rectifier efficiency (η)

g. Ripple factor (ɤ).

AU : Dec.-16, Marks 8

3. Define the following terms

i) Transformer utilization factor

ii) Ripple factor of HWR with resistive load and derive the expression for the same.

4. What are the disadvantages of a half wave rectifier circuit ?

5. Show that for a half wave circuit

%η = 40.6 / (1 + R_f/R_L) % where R_f is forward resistance of diode and RL is the load resistance.

6. Draw the circuit diagram of half-wave rectifier and explain it's operation with necessary wave form. Also derive expression for rectification efficiency and transformer utilisation factor.

AU : May-12, Marks 10

7. A voltage V = 300 cos 1001 is applied to a half wave rectifier, with RL = 5kti. The rectifier may be represented by ideal diode in series with a resistance of lkΩ,. Calculate

i) I_m  ii) D.C. power iii) A.C. power iv) Rectifier efficiency and v) Ripple factor.

[Ans.: 50 mA, 1.2665 watts, 3.75 watts, 33.77 %, 1.211]