Heat Flow in a Cable

Heat Flow in a Cable

As seen earlier, the current in the cable, dielectric loss and sheath loss together cause the increase in the temperature of the cable. The heat produced due to increase in temperature must be dissipated to the soil. When rate of heat generation and dissipation becomes equal then temperature becomes constant. This temperature infact is the important factor for deciding current carrying capacity of the cable.

The path for the heat dissipation is through the dielectric, then sheath, bedding, serving and finally into the surrounding soil or air. The heat flow in a 3 phase belted cable is shown in the Fig. 6.11.1 (a) while heat flow due to a three single core cable to ground is shown in the Fig. 6.11.1 (b).

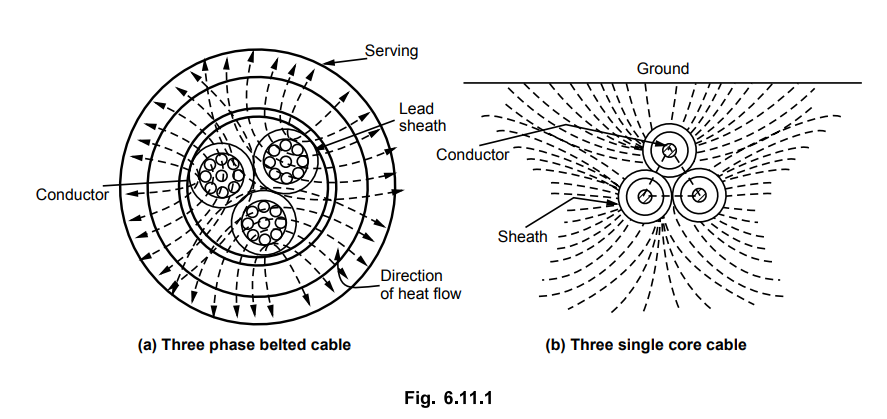In case of three phase belted cable, the heat flows through three parallel paths and all the three conductors are at same temperature.

The overall heat flow in a cable is similar to the flow of leakage current in an electric circuit ; flowing radially out from core to ground through dielectric, sheath, bedding, armouring and serving.

1. Thermal Characteristics of Cable

The current in an electric circuit is given by,

I = Potential difference / Resistance  = V/R

Similarly heat flow H is given by,

H = Temperature difference / Thermal resistance = θ/S

Thermal resistance S is defined as the resistance which allows the heat flow of 1 watt when a temperature difference of 1 °C is maintained. It is given by,

S = kl / A thermal ohms

where  k = Thermal resistivity of the material

l = Length of the path of heat flow

A = Area of section through which heat flows

The thermal resistivity is expressed in ^oC/watt/cm

Consider the equivalent circuit for heat flow in a three phase cable as shown in the Fig. 6.11.2.

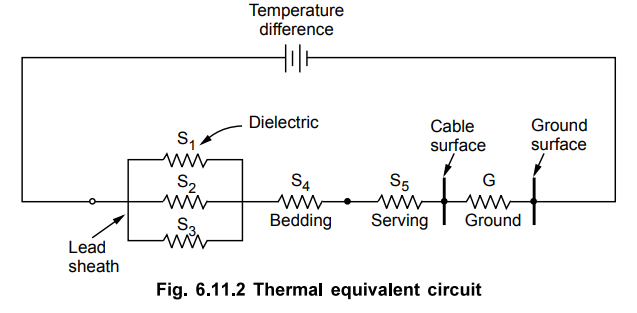
The total temperature difference is difference between conductor temperature and ambient temperature. The S₁, S₂ and S₃ are thermal resistances of the three dielectric paths which are in parallel. Then heat flows through bedding whose thermal resistance is S₄. Finally it flows trough serving whose thermal resistance is S₅. The G represents the thermal resistance of ground to ambient temperature. The current carrying capacity of cables depends on the heat dissipation and to calculate it, it is necessary to obtain the thermal resistances of various parts through which heat flows.

2. Thermal Resistance of Single Core Cable

Consider a single core cable as shown in the Fig. 6.11.3. Let

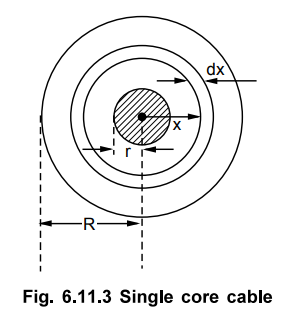
The value of k for the cables above 22 kV is 550 while it is 750 for pressure upto and including 22 kV.

It is difficult to find the expression for the thermal resistance of three core cable. The empirical formula given by Simon is,

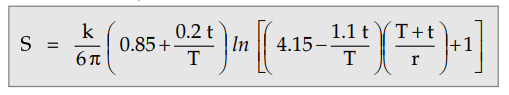
 where T = Thickness of the conductor insulation

t = Thickness of the belt insulation

r = Radius of the conductor

3. Thermal Resistance of Soil

The thermal resistance of the soil depends on the nature of the soil and its moisture content. Hence exactly thermal resistance can not be obtained for the soil. Assuming the ground to be isothermal and homogeneous, the thermal resistance of ground is given by,

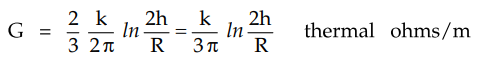where k = Thermal resistivity of soil

h = Depth of cable axis below the soil

R = Radius upto lead sheath i.e. overall radius

In practice it is necessary to multiply value of k by 2/3 which is obtained in the laboratory, to obtain actual value of G.

Review Questions

1. Explain the thermal characteristics of a cable.

2. Write a note on heat flow in a cable.