Hopkinson's Test

Hopkinson's Test

AU: Dec.-05,06,08,09,16,19, May-07,14,16

• This test is called regenerative test or back to back test which can be carried out on two identical d.c. machines mechanically coupled to each other and simultaneously tested. Thus the full load test can be carried out on two identical shunt machines without wasting their outputs. One of the machines is made to act as a motor while the other as a generator. The mechanical output obtained from the motor drives the generator whose electrical output supplies the greater part of input to the motor. The motor is connected to the supply mains only to compensate for losses since in absence of losses, the motor-generator set would have run without any external power supply. But due to losses, the generator output is not sufficient to drive the motor. Thus motor takes current from the supply to account for losses.

• The Fig. 5.8.1 shows the connection diagram for Hopkinson's test. The two shunt machines are connected in parallel. One of the machines is then started as a motor. Here the startor connections are not shown for simplicity.

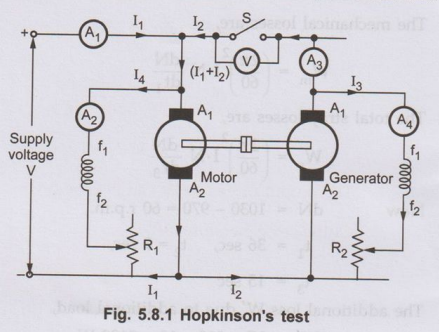
• The switch S is kept open. The other machine which is coupled to first will act as load on first which is acting as motor. Thus second machine will act as a generator. The speed of motor is adjusted to normal value with the help of the field rheostat. The voltmeter reading is observed. The voltage of the generator is adjusted by its field rheostat so that voltmeter reading is zero. This will indicate that the generator voltage is having same magnitude and polarity of that of supply voltage. This will prevent heavy circulating current flowing in the local loop of armatures on closing the swi5ztch. Now switch S is closed. The two machines can be put into any load by adjusting their field rheostats. The generator current I₂ can be adjusted to any value by increasing the excitation of generator or by reducing the excitation of motor. The various readings shown by different ammeters are noted for further calculations.

• The input to the motor is nothing but the output of the generator and small power taken from supply. The mechanical output given by motor after supplying losses will in turn drive the generator.

Let V = Supply voltage

I₁ = Current taken from the supply,

I₂ = Current supplied by generator

I₃ = Exciting current of generator,

I₄ = Exciting current of motor

R_a = Resistance of armature of each machine

η = Efficiency of both generator and motor.

But the assumption of equal efficiencies of two machines is true in case of only large output machines where difference in armature currents of two machines is not large. Also the difference in excitation current required to circulate full load current in the armature will not affect the iron losses. But in case of small machines the difference between armature and field currents is large. So efficiencies cannot be assumed to be same. Here the stray losses are assumed to be equal whereas armature and field copper losses are separately determined for estimating the efficiencies separately.

Armature copper loss in generator = (I₂ + I₃)² R_a

Armature copper loss in motor = (I₁ + I₂ −1₄)²

 Copper loss in field winding of generator = V I₃

Copper loss in field winding of motor = V I₄

But total losses in generator and motor are equal to the power supplied by the mains.

Power drawn from supply = V I₂

The stray losses of both machines can be calculated as, ananigol

Total stray loss for both the machines = VI₂ − [(I₂ + I₃)² R_a + (I₁ + I₂ – I₄)² R_a + VI₃ + VI₄] = W_s(say)

Assuming that stray losses are equally divided between the two machines.

Stray loss for each machine = W_s/2

1. Advantages

The various advantages of Hopkinson's test are,

1. The power required for conducting the test is small compared to full load powers of the two machines.

2. Since the machines are operated at full load conditions, change in iron loss due to distortion in flux at full load will be included in the calculations.

3. As the machines are tested under full load conditions, the temperature rise and quality of commutation of the two machines can be observed.

4. The test is economical as power required to conduct the test is very small which is just sufficient to meet the losses.

5. There is no need for arranging any actual load. Similarly by changing the field currents of two machines, the load can be easily changed and a load test over complete range of load can be taken.

2. Disadvantages

The various disadvantages of Hopkinson's test are,

1. There is difficulty in availability of two identical machines.

2. The iron losses in the two machines cannot be separated. The iron losses are different in both the machines because of different excitations.

3. The machines are not loaded equally in case of small machines which may lead to difficulty in analysis.

This test is better suited in case of large machines.

Ex. 5.8.1 The Hopkinson's test on two shunt machines gave the following results for full load conditions. Line voltage 250 volts, line current excluding field currents is 50 A, motor armature current 380 A, field currents 5 A, 4.2 A respectively. Calculate the efficiency of each machine. Armature resistance of each machine is 0.02 Ω AU : Dec. -08, Marks 8

Sol. : The connections and current distribution is shown in the Fig. 5.8.2.

Ex. 5.8.2 In a Hopkinson's test on a pair of 500 V, 100-kW shunt generators, the following data was obtained: Auxiliary supply, 30 A at 500 V: Generator output current, 200 A Field currents, 3.5 A 1.8 A Armature circuit resistances, 0.075 each machine. Voltage drop at brushes, 2 V (each machine). Calculate the efficiency of the machine acting as a generator. AU : Dec.-16

Sol. :  V = 500 V, P = 1000 kW

Review Questions

1. Explain the Hopkinson's test for determining efficiency of two similar d.c. shunt machines. State its merits and demerits. AU: Dec.-06, 09, 19, May-16, Marks 8

2. The following results were obtained from Hopkinson's test on two similar d.c. machines: Supply voltage 400 V, line current 50 A. Generator armature current 250 A, field currents 2.4 and 2.5 A. Estimate the efficiency of each machine on the loads of the test. Armature resistance of each machine is 0.1 Ω. AU: Dec.-05 (Ans.: 2375 W, 89.72 %, 91.22%)

3. The following results were obtained during Hopkinson's test on two similar 230 V machines; armature currents 37 A and 30 A; field currents 0.85 A and 0.8 A. Calculate the efficiencies of machines if each has armature resistance of 0.33 Ω.

(Ans.: 647.27 W, 481 W, 430.615 W, η_m = 87.61%)

4. Explain back to back test as two identical DC machines and calculate the efficiency of the machines as generator and motor. Mention the advantages of this test over the other tests.

5. The Hopkinson's test on two shunt machines gave the following results for full load conditions. Line voltage 250 volts, line current excluding field currents is 50 A, motor armature current 380 A, gfield currents 5 A, 4.2 A respectively.

Calculate the efficiency of each machine. Armature resistance of each machine is 0.02 Ω. (Ans.: 92.03 %, 92.02%)

6. The Hopkinson's test on two similar d.c. shunt machines gave the following results :

Line voltage = 220 V, Line current excluding field current = 40 A,

Armature current of motoring machine = 200 A, Field currents 6 A and 7 A.

Calculate the efficiency of each of the machines at the given load conditions. The armature resistance of each of the machines is 0.05 Ω. (Ans.: 86.75 %, 85.78%)

7. What are the merits and demerits of Hopkinson's test ?AU : May-14, Marks 4