Illustrative Problems

Illustrative Problems

AU: Dec-.19, Marks 8

In this section we will discuss various algorithms with the help of illustrative examples :

 

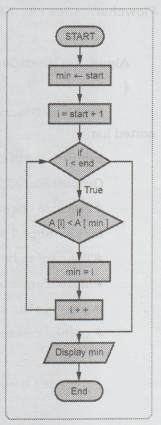
1. Finding a minimum in a list

Algorithm FindMin

{

Problem Description : Finding the minimum element in a list Input : A list of elements in an array A[start...end]

Output: minimum element

min<- start

for i from start+1 to end do

if A[i]<A[min] then

min < -i

end if

end for

}

Write("The minimum element is present at position "+min)

2. Insert a card in a list of sorted cards

Consider the cards are sorted in following manner

Step 1: Traverse the cards from first card to last card. Find the cards having value greater than keycard Shift those cards one position ahead.

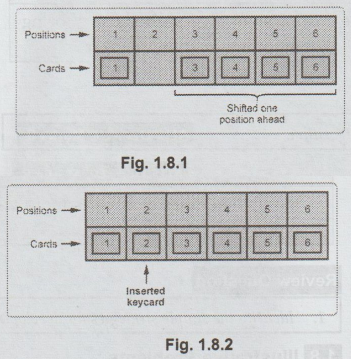
Fig. 1.8.1

Fig. 1.8.2

Flowchart : (See Fig. 1.8.3 on next page)

Algorithm InsertCard

{

Problem Description : Inserting a card at appropriate position in the list of already sorted list

Input: A list of elements in an cards A[start...end]

Output: Sorted List A

#Traverse the cards from 1 to length(A)

for i in range 1 to len(A)

#The card to be placed is called keyCard

#Move elements of arr[0..i-1], that are

# greater than key, to one position ahead

# of their current position

j=i-1

while j > = 0 and keyCard < A[j]:

A[j+1] = A[j]

j = j-1

A[j+1] = keyCard

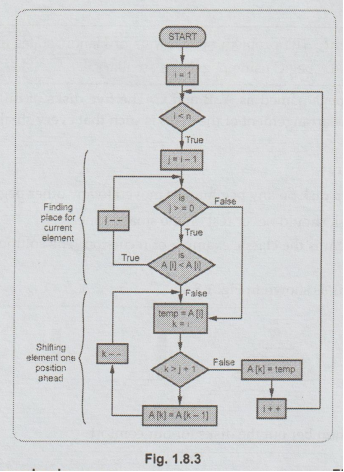
Fig. 1.8.3

 

3. Guess an integer number in a range Algorithm Guess Number

{

#Problem Description: Guess the correct number

#Input: Key element num

Output: Message about the guessing made

num = random.randint(1, 10)

while True:

print('Guess a number between 1 and 10')

Read(i)

if i == num;

print('You have guessed correct number!!!')

break

else if i < num:

print('Number is lower enter higher)

else if i > num:

print('Number is higher enter lower')

}

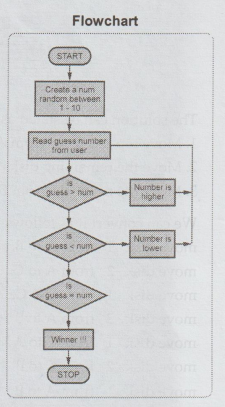
Flowchart

 

4. Towers of Hanoi

Problem Statement : The problem of " Towers of Hanoi" states that move the five disks from peg A to peg C using peg B as a auxillary.

There are three pegs named as A, B and C. The five disks of different diameters are placed on peg A. The arrangement of the disks is such that every smaller disk is placed on the larger disk.

The conditions are :

i) Only the top disk on any peg may be moved to any other peg.

ii) A larger disk should never rest on the smaller one.

The above problem is the classic example of recursion. The solution to this problem is very simple.

The initial setup is as shown in Fig. 1.8.4

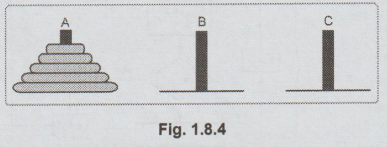
Fig. 1.8.4

First of all let us number out the disks for our comfort

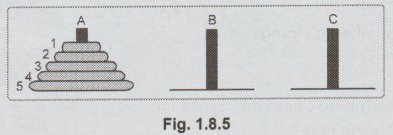
Fig. 1.8.5

The solution can be stated as,

1. Move top n-1 disks from A to B using C as auxillary

2. Move the remaining disks from A to C.

3. Move the n-1 disks from B to C using A as auxillary.

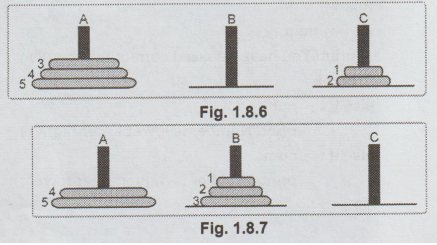
Fig. 1.8.6

Fig. 1.8.7

We can convert it as follows

move disk 1 from A to B.

move disk 2 from A to C.

move disk 1 from B to C.

move disk 3 from A to B

move disk 1 from C to A

move disk 2 from C to B

move disk 1 from A to B

move disk 4 from A to C

move disk 1 from B to C

move disk 2 from B to A

move disk 1 from C to A

move disk 3 from B to C

move disk 1 from A to B

move disk 2 from A to C

move disk 1 from B to C

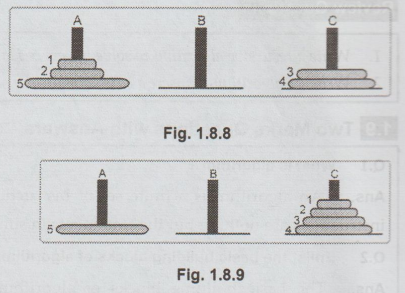
Fig. 1.8.8

Fig. 1.8.9

Thus actually we have moved n-1 disks from peg A to C. In the same way we can move the remaining disk from A to C.

This is a problem in which recursion is used.

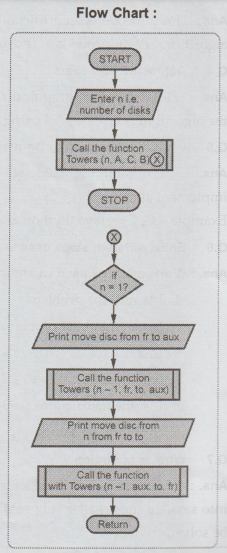
Algorithm TowerofHanoi

{

Write("\n\n Enter the total number of disks"); Read(n);

towers(n,'A','C','B');

}

Subroutine towers(n,fr,to,aux)

{

#if only one disk has to be moved if n= =1

{

Write(from, to);

return;

}

#move top n-1 disks from A to B using C

towers(n-1,from,aux,to);

Write(from, to);

# move remaining disk from B to C using A

towers(n-1, aux,to,fr);

}

Flow Chart :

Review Questions

1. Write a recursive algorithm to solve towers of Hanoi problem. AU : Dec-.19, Marks 8

2. Write an algorithm to insert a card into a list of sorted cards. AU : Dec.-.19, Marks 8