Inductance - Self Inductance and Mutual Inductance

Inductance - Self Inductance and Mutual Inductance

AU : May-12, Dec.-04, 12, 14, 16

• A wire or conductor of certain length, when twisted into coil becomes a basic inductor. For every conductor carrying current I and producing magnetic field  , there exists a self inductance. When two such coils are placed very close to each other, there exists a mutual inductance between the two. In this section, we will discuss the concept to self inductance and mutual inductance.

 

1. Self Inductance

• When a closed conducting path or a circuit carries current I, a magnetic field B is produced. This causes a magnetic flux ϕ which is given by,

In the circuit or slosed path consists N turns, the flux produced by the magnetic field  , links with each turn of the circuit. The flux linkage is defined as the product of number of turns N and the total flux ϕ  linking each of the turn. It is denoted by λ and is measured in weber turn (Wb • t). Hence we can write, 

λ = N . ϕ wb . t ….. (8.10.2)

• The flux linking with each turn of the circuit is proportional to the current flowing through the circuit. The flux linkage with the circuit of N turns, carrying current I is as shown in the Fig. 8.10.1.

• The ratio of the total flux linkage to the current flowing through the circuit is called inductance and it is given by,

L = (N ϕ / I = λ / I ) H ...(8.10.3)

• The inductance is also known as self-inductance of the circuit as the flux produced by the current flowing through the circuit links with the same circuit. The self inductance or inductance is measured in henry (H) which is equivalent to one weber-turn/ampere (Wb-1 /A).

 

2. Mutual Inductance

• Consider that two different circuits with self inductances L₁ and L₂ are kept close to each other as shown in the Fig. 8.10.2. Let N₁ and N2 be the number of turns for the two circuits and let I₁ and I₂ be the currents through two circuits as shown in the Fig. 8.10.2.

• As two circuits are placed very close to each other, these circuits interact magnetically with each other. The flux produced by circuit 1, due to current I flowing through it, is denoted by 911. Similarly the flux produced by circuit 2, due to the current I₂ flowing through it, is denoted by ϕ₂₂. The flux produced by each circuit links with the circuit itself and the other circuit too. The part of flux ϕ₁₁ that links with circuit 2 is denoted by ϕ₁₂. Similarly the part of flux ϕ₂₂ that links with circuit is denoted by ϕ₂₁. The mutual inductance between the two circuits is defined as the flux linkage of to the current in other circuit. Thus the inductance M₁₂ is given by,

M₁₂ = Flux linkage of circuit 1 / Current in circuit 2

= N₁ ϕ₂₁ / I₂  ….. (8.10.4)

• Similarly the mutual inductance M₂₁ is given by,

M₂₁ = Flux linkage of circuit 2 / Current in circuit 1

= N₂ ϕ₁₂ / I₁  ….. (8.10.5)

• If the medium surrounding two circuits is linear without ferromagnetic material, then the mutual inductances represented in equations (8.10.4) and (8.10.5) are equal. Thus for linear medium around two circuits, we can write,

M₁₂ = M₂₁ = M ….. (8.10.6)

• The mutual inductance between two magnetic circuits depends on the magnetic interaction existing between the two circuits. Similar to the self inductance, the mutual inductance is also measured in henry (H) which is equivalent to one weber-tum per ampere (Wb-1 /A).

 

3. Coefficient of Coupling between Two Circuits

• When the two magnetic circuits kept closed to each other interacts with each other magnetically through the flux linkages in the circuit due to the current in other circuit then the circuits are called magnetically coupled circuits.

• Consider an example of the magnetically coupled circuits discussed in section 8.10.2. The self inductances of the circuit 1 and circuit 2 are given by,

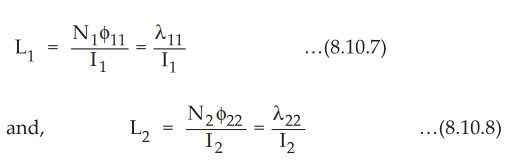
• The flux linking with circuit 2 due to current in circuit 1 is denoted by ϕ₁₂. This flux is actually the part of the total flux produced by the current in the circuit 1. Hence we can write,

ϕ₁₂ = K₁ ϕ₁₁ .....(8.10.9)

• Similarly for the flux ϕ₂₁ which is the part of flux ϕ₂₂ can be written as,

Φ₂₁ = K₂ ϕ₂₂          ...(8.10.10)

• Rewriting the expressions for the mutual inductances as follows,

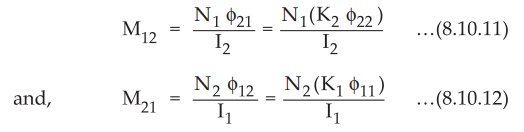
• Assuming linear medium surrounding two circuits, we can write,

M₁₂ = M₂₁ = M

Hence we can write,

where K is called coefficient of coupling between two coils.

Hence we can write,

K = M / √L₁L₂ .....(8.10.14)

 

4. Inductance of a Solenoid

• Consider a solenoid of N turns as shown in the Fig. 8.10.3.

• Let the current flowing through the solenoid be I ampere. Let the length of the solenoid be I and the cross-sectional area be A.

• From the results obtained in previous sections, the field intensity inside the solenoid is given by,

H = N_I / l A/m       ... (8.10.15)

• The total flux linkage is given by,

Total flux linkage = N ϕ = N (B) (A) = N (μH) (A)

Total flux likage = μ NHA = μN[NI / l] A

= μN²IA / l  ... (8.10.16)

• Thus the inductance of a solenoid is given by,

L = Total flux linkage / Total current = μN²IA / l(I)

L = ( μN²IA / l ) H ….. (8.10.17)

 

5. Inductance of a Toroid

• Consider a toroidal ring with N turns and carrying current I. Let the radius of the toroid be R as shown in the Fig. 8.10.4.

• The magnetic flux density inside a toroidal ring is given by,

B = µNI / 2 πR  ….. (8.10.18)

• The total flux linkage of a toroidal ring having N turns is given by,

Total flux linkage = N ϕ

But ϕ = (B) (A) where A = Area of cross-section of a toroidal ring

Total flux linkage = N (B) (A)

The inductance of a toroid is given by,

L = Total flux linkage / Total current = μN²IA / (2 πR) (I)

L = μN²IA / (2 πR) H ….. (8.10.19)

where A = Area of cross-section of a toroidal ring = πr² m²

• For a toroid with N number of turns h as the height of toroid with r₁ as inner radius and r₂ as outer radius, the inductance is given by

L = (μN²h / 2 π) ln (r₂ / r₁ ) H ….. (8.10.20)

 

6. Inductance of a Co-axial Cable

• Consider a co-axial cable with inner conductor radius a and outer conductor radius b as shown in the Fig. 8.10.5. Let the current through the coaxial cable be I.

• For the co-axial cable the field intensity at any point between inner and outer conductors is given by,

H = I / 2 πr  where a < r < b ... (8.10.21)

But B = µH = µI / 2 πr  ... (8.10.22)

• Now assume that the axis of the cable is along z-axis as shown in Fig. 8.10.5. The magnetic flux density will be in radial plane extending from r = a to r = b and z = 0 to z = d.

The inductance of a co-axial cable may be expressed per unit length as,

 

Ex. 8.10.1 Calculate the inductance of a solenoid of 200 turns wound tightly on a cylindrical tube of 6 cm diameter. The length of the tube is 60 cm and the solenoid is in air.

Sol. : For a given solenoid in air, μ = μ0 = 4л × 10-7 Wb/A.m, N = 200

d = 6 cm = 6 × 10-2m hence

r = d/2 3 × 10−2 m, l = 60 cm = 60 × 10−2 m hence

The inductance of a solenoid is given by,

 

Ex. 8.10.2 Calculate the inductance of a ring shaped coil of mean diameter 20 cm, wound on a wooden core of 2 cm diameter containing 200 turns.

AU : Dec.-16, Marks 8

Sol. : Coil diameter = 20 cm,core diameter = 2 cm, µr = 1

Ex. 8.10.3 A solenoid has an inductance of 20 mH. If the length of the solenoid is increased by two times and the radius is decreased to half of its original value, find the new inductance.

Sol. : The inductance of the solenoid is given by,

L = μN²A / l  = 20 mH

Now length is made 2l while the radius is made | Then the inductance is given by,

 

Ex. 8.10.4 Calculate the self inductance of infinitely long solenoid.

Sol. : For infinitely long solenoid, the magnetic flux density inside the solenoid per unit length is,

B = µH = µIN / l = µIn   ... (1)

Where n = N / l

= Number of turns per unit length.

Assume that A is the cross-sectional area of the solenoid, then the total flux through the cross-section is,

ϕ = BA = µInA     ... (2)

But the flux represented by equation (2) is the flux for a unit length of solenoid. The flux linkage per unit length is,

Ex. 8.10.5 A coil of 500 turns is wound on a closed iron ring of mean radius 10 cm and cross-section area of 3 cm2. Find the self inductance of the winding if the relative permeability of iron is 800.

Sol. : For a toroidal ring of iron,

Ex. 8.10.6 An air-core toroid with rectangular cross-section, has 700 turns, with inner radius of 1 cm and outer radius of 2 cm and height is 1.5 cm. Find inductance using 1) The formula for sq. cross section of toroids 2) The approximate formula for general toroid, which assumes a uniform H at mean radius.

Sol. : N = 700, h = height = 1.5 cm = 1.5 × 10^-2m

r₁ = Inner radius = 1 cm = 1 × 10^-2m  r₂ = Outer radius = 2 cm = 2 × 10^-2m

1) In general, inductance of a toroid of square cross section is given by,

= 1.0189 mH

2) By general approximate formula for toroid, the inductance is given by,

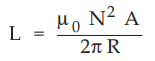
where A = Area of square cross-section = (1 cm) (1.5 cm) = 1.5 × 10^{- 4} m²

r = Mean radius = 1.5 cm = 1.5 × 10^{- 2} m

L = 4 × π × 10^-7 × (700)² × (1.5 × 10^-4) / 2 × π × 1.5 × 10^-2

= 0.98 mH

Thus for toroid, with radius larger than the cross-section, the inductance obtained by both formulae are approximately same.

 

Ex. 8.10.7 An air core toroid has circular cross section of 4 mm radius. Find the inductance if there are 2500 turns and the mean radius is 20 mm.

Sol. : Mean radius R = 20 mm = 20 × 10^-3 m ,

N = 2500

Radius of cross-section r = 4 mm = 4× 10^-3  m,

N = 2500

For air, µ r = 1

The inductance of toroid is given by,

 

Ex. 8.10.8 The core of a toroid is of 12 cm² area and is made up of material with µ_r = 200. If the mean radius of the toroid is 50 cm, calculate the number of turns needed to obtain an inductance of 2.5 H.

Sol. :

 

Ex. 8.10.9 Find inductance per unit length of a co-axial cable if radius of inner and outer conductors are 1 mm and 3 mm respectively. Assume relative permeability unity.

Sol. : For a co-axial cable, the inductance per unit length is given by,

 

Ex. 8.10.10 Calculate the inductance of a 10 m length of co-axial cable filled with a material for which µr = 80 and radii of inner and outer conductors are 1 mm and 4 mm respectively.

Sol. :

 

Ex. 8.10.11 A solenoid with N₁ = 2000, r₁ = 2 cm and li = 100 cm is concentric within a second coil of N₂ = 4000, r₂ = 4 cm and l₂ = 100 cm. Find mutual inductance assuming free space conditions.

Sol. : For a solenoid with large length as compared to small cross section, the magnetic field intensity inside the coil can be assumed to be constant and zero for points just outside the solenoid.

Let the current flowing through the coil be I₁

Then the magnetic field intensity is given by,

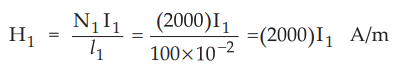
The magnetic flux density is given by,

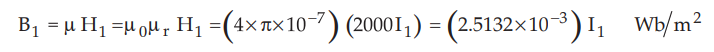
Total flux produced is given by,

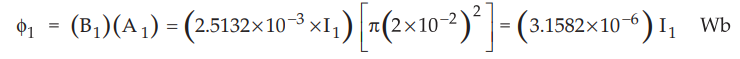
The flux calculated above can only link with the second coil as H₁ and B₁ are zero outside the coil 1.

The mutual inductance between two coils is given by,

 

Ex. 8.10.12 The magnetic circuit of an iron ring with mean radius of 10 cm has a uniform cross-section of 10^-3 m². The ring is wound with two coils. If the circuit is energized by a current i₁ (t) = 3 sin 100π t A in the first coil with 200 turns, find the induced emf in the second coil with 100 turns. Assume that µ = 500 µ₀.

AU : Dec.-14, Marks 4

Sol. : For toroid 1 :

 

Examples for Practice

Ex. 8.10.13 Calculate the inductance of a solenoid of 200 turns wound tightly on a cylindrical tube of 6 cm diameter. The length of the tube is 60 cm and the solenoid is in air.

[Ans.: 0.2368 mH]

Ex. 8.10.14 An air-core toroid with rectangular cross-section, has 700 turns, with inner radius of 1 cm and outer radius of 2 cm and height is 1.5 cm. Find inductance using i) The formula for square cross section of toroids ii) The approximate formula for general toroid, which assumes a uniform H at mean radius.

[Ans.: 1.0189 mH, 0.98 mH]

Ex. 8.10.15 A solenoid with Ni = 2000, r^ = 2 cm and Il = 100 cm is concentric within a second coil of N2 = 4000, r2 = 4 cm and 12 = 100 cm. Find mutual inductance assuming free space conditions.

[Ans.: 12.633 mH]

Review Questions

1. Derive the expressions for the inductance of

i) Solenoid ii) Toroid iii) Co-axial cable.

2. Write a note on mutual inductance.

3. Derive expression for inductance of a toroid.

AU : Dec.-04, Marks 10

4. Find self inductance of a solenoid.