Induction Motor as a Transformer

Induction Motor as a Transformer

We know that, transformer is a device in which two windings are magnetically coupled and when one winding is excited by a.c. supply of certain frequency, the e.m.f. gets induced in the second winding having same frequency as that of supply given to the first winding. The winding to which supply is given is called primary winding while winding in which e.m.f. gets induced is called secondary winding. The induction motor can be regarded as the transformer.

The difference is that the normal transformer is an alternating flux transformer while induction motor is rotating flux transformer. The normal transformer has no air gap as against this an induction motor has distinct air gap between its stator and rotor. 

In an alternating flux transformer the frequency of induced e.m.f. and current in primary and secondary is always same. However in the induction motor frequency of e.m.f. and current on the stator side remains same but frequency of rotor e.m.f. and current depends on the slip and slip depends on load on the motor. So we have a variable frequency on the rotor side. But it is important to remember that at start when N = 0 the value of slip is unity (s = 1), then frequency of supply to the stator and of induced e.m.f. in the rotor is same. The effect of slip on the rotor parameters is already discussed in the previous section.

And last difference is that in case of the alternating flux transformer the entire energy present in its secondary circuit, is in the electrical form. As against this, in an induction motor part of its energy in the rotor circuit is in electrical form and the remaining part is converted into mechanical form.

In general, an induction motor can be treated as a generalized transformer as shown in the Fig. 5.8.1. In this, the slip ring induction motor with star connected stator and rotor is shown.

So if  E₁= Stator e.m.f. per phase in volts.

E₂ = Rotor induced e.m.f. per phase in volts at start when motor is at standstill.

Then according to general transformer there exists a fixed relation between E₁ and E₂ called transformation ratio.

At start when N = 0, s = 1

and we get, 

Key Point So if stator supply voltage is known and ratio of stator to rotor turns per phase is known then the rotor induced e.m.f on standstill can be obtained.

Example 5.8.1 For a 4 pole, 3 phase, 50 Hz induction motor ratio of stator to rotor turns is 2. On a certain load, its speed is observed to be 1455 r.p.m. when connected to 415 V supply. Calculate,

i) Frequency of rotor e.m.f. in running condition

ii) Magnitude of induced e.m.f. in the rotor at standstill

iii) Magnitude of induced e.m.f. in the rotor under running condition.

Assume star connected stator.

Solution : The given values are, K = rotor tums/stator turns = 1/2 = 0.5 and

P = 4, f = 50 Hz, N = 1455 r.p.m., E_1line = 415 V

ii) At standstill, induction motor acts as a transformer so,

E _2ph / E _1ph  = Rotor turns / Stator turns = K

But ratio of stator to rotor turns is given as 2, i.e.

N₁ / N₂ = 2

N₂ / N₁ = ½ = K   

and    E_{1 line} =  415 V

The given values are always line values unless and until specifically stated as per phase.

iii) In running condition,

E_2r = s E₂ = 0.03 × 119.8 = 3.594 V

The value of rotor induced e.m.f. in the running condition is also very very small.

Example 5.8.2 A 3-phase induction motor with star connected rotor has induced electromotive force of 60 V between slip rings at standstill on open circuit with normal voltage applied to the stator. The resistance and standstill leakage reactance of each rotor phase are 0.6 Ω and 4 Ω respectively. Calculate the current per phase in the rotor :

i) When it is at standstill and connected to a resistance of 5 Ω and reactance of 2 Ω per phase and

ii) When running with a slip of 4 % with its rotor terminals short circuited.

Solution : The e.m.f. between the slip rings = E₂ = 60 V, R₂ = 0.6 Ω, X₂ = 4 Ω

i) Rotor standstill and R_x = 5 Ω, X_x = 2 Ω added externally.

The equivalent circuit is shown in the Fig. 5.8.2.

This is rotor current per phase.

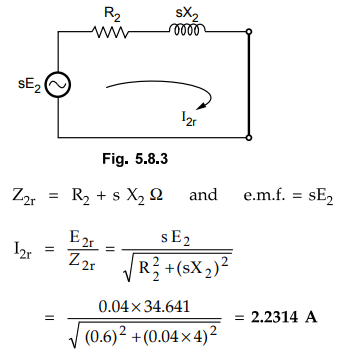
ii) s = 4 % i.e. 0.04 and rotor terminals shorted.

Rotor terminals shorted means external resistance and reactance completely removed.

R_x = X_x = 0 Ω

 This is shown in the Fig. 5.8.3.

Example 5.8.3 A 1000 V, 50 Hz, 3 phase slip ring induction motor has star connected stator. The ratio of stator to rotor turns is 3.6. The rotor standstill impedance is 0.01 + j 0.2 Ω. Calculate the external resistance per phase required in rotor circuit to limit starting rotor current to 200 A.

Solution : The given values are,

Let at start R_x be the external resistance per phase, introduced in rotor circuit.

R’₂ = R₂ + R_x        ... At start

Example for Practice

Example 5.8.4 A 3 phase, 4 pole, 50 Hz, induction motor has slip ring rotor. The rotor winding is star connected with 0.2 Q of resistance per phase and standstill reactance of 1 Q per phase. Its open circuit e.mf. between the slip rings is 120 V, when stator is excited by a rated voltage. Its full load speed is 1440 r.p.m. Find the rotor current and rotor power factor.

i) At start and ii) On full load condition.

[Ans.: 67.93 A per phase, 13.586 A] 

Review Question

1. Induction motor is a generalised transformer. "Justify the statement.