Electric Circuit Analysis: Unit III: Transient Response Analysis
Initial (boundary) condition for capacitors
Transient Response Analysis
When the capacitor has no initial charge or voltage, Q(0-) = 0 and Vc(0-) = 0. Therefore, from equations (9) and (10), Vc (0+) = q(0+) = 0.
INITIAL (BOUNDARY) CONDITION FOR CAPACITORS
We
know that, ic (t) = C dVc (t) / dt … (5)
To
determine the capacitor voltage in terms of capacitor current, we write.
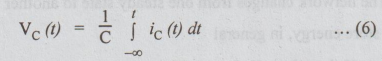
The
above expression states that the voltage at any time t, is proportional to the
integral of the current through the capacitor.
At t = 0+
The
interval from 0 to 0+ is almost zero. If ic is finite and does not contain
impulses or derivatives.
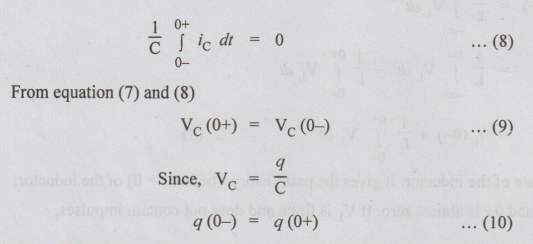
We
conclude that the voltage and hence the charge across the capacitor can not
change instantaneously. But the capacitor current has no such restriction.
ic
(0+) ≠ ic (0-)
When
the capacitor has no initial charge or voltage, Q(0-) = 0 and Vc(0-) = 0.
Therefore, from equations (9) and (10), Vc (0+) = q(0+) = 0.
Thus,
the capacitor with no initial voltage or charge behaves like a short circuit at
t = 0+.
The
capacitor with an initial charge qc (0-) = Qo is equivalent to a
voltage source of value Vco = Q0 / C at t = 0+.
Electric Circuit Analysis: Unit III: Transient Response Analysis : Tag: : Transient Response Analysis - Initial (boundary) condition for capacitors
Electric Circuit Analysis: Unit III: Transient Response Analysis
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation