Input and Output Resistance

Input and Output Resistance

 

1. Input resistance

• If the feedback signal is added to the input in series with the applied voltage (regardless of whether the feedback is obtained by sampling the output current or voltage), it increases the input resistance.

• Since the feedback voltage Vf opposes Vs, the input current I; is less than it would be if Vf were absent, as shown in the Fig. 9.9.1

• Hence, the input resistance with feedback Rif = Vs / Ii is greater than the input resistance without feedback, for the circuit shown in Fig. 9.9.1.

• On the other hand, if the feedback signal is added to the input in shunt with the applied voltage (regardless of whether the feedback is obtained by sampling the output voltage or current), it decreases the input resistance.

• Since Is = Ii + If, the current Is drawn from the signal source is increased over what it would be if there were no feedback current, as shown in the Fig. 9.9.2.

• Hence, the input resistance with feedback

is decreased for the circuit shown in Fig. 9.9.2. Now we see the effect of negative feedback on input resistance in different topologies (ways) of introducing negative feedback and obtain R^ quantitatively.

 

Ex. 9.9.1 Derive the expression for input resistance for a voltage series feedback.

Sol. : Step 1 : Draw the equivalent circuit for voltage series amplifier.

• The voltage series feedback topology shown in Fig. 9.9.3 with amplifier is replaced by Thevenin's model. Here, Av represents the open-circuit voltage gain taking Rs into account.

• Since throughout the discussion of feedback amplifiers we will consider Rs to be part of the amplifier and we will drop the subscript on the transfer gain and input resistance (A_v instead of A_vs and R_if instead of R_ifs)

• Look at Fig. 9.9.3 the input resistance with feedback is given as

R_if = V_s / I_i … (1)

Step 2 : Obtain expression for V_s .

Applying KVL to the input side we get,

Step 3 : Obtain expression for V_o in terms of I_i.

The output voltage I_o is given as

Important Concept

A_v represents the open circuit voltage gain without feedback and A_V is the voltage gain without feedback taking the load R_L into account.

Step 4 : Obtain expression for R_if.

Substituting value of Vo from equation (3) in equation (2) we get,

 

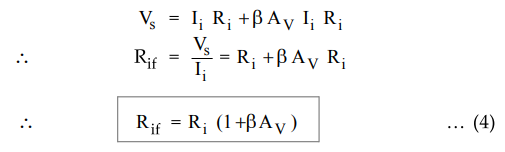
Ex. 9.9.2 Derive the expression for input resistance for a current series.

Sol. : Step 1 : Draw the equivalent circuit for current series feedback amplifier.

• The current series feedback topology is shown in Fig. 9.9.4 with amplifier input circuit is represented by Thevenin's equivalent circuit and output circuit by Norton's equivalent circuit.

• Looking at Fig. 9.9.4 the input resistance with feedback is given as

Rif = V_s / I_i

Step 2 : Obtain expression for V_s .

Applying KVL to the input side we get,

Step 3 : Obtain expression for I_o in terms of V_i.

The output voltage I_o is given as

Important Concept

G_m represents the open circuit voltage gain without feedback and G_M is the voltage gain without feedback taking the load R_L into account.

Step 4 : Obtain expression for R_if.

Substituting value of I_o from equation (2) in equation (1) we get,

 

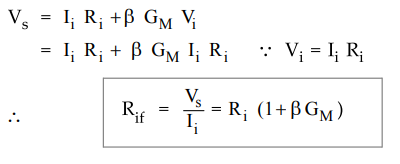
Ex. 9.9.3 Derive the expression for input resistance for a current shunt feedback.

 Sol. : Step 1 : Draw the equivalent circuit current shunt amplifier.

The current shunt feedback topology is shown in Fig. 9.9.5 with amplifier input and output circuit replaced by Norton's equivalent circuit.

Step 2 : Obtain expression for l_s.

Applying KCL at input node we get,

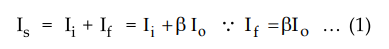
Step 3 : Obtain expression for V_o in terms of I_i

The output current I is given as

 

Important Concept

A_i represents the open circuit current gain without feedback and A_I is the current gain without feedback taking the load R_L into account.

Step 4 : Obtain expression for R_if.

Substituting value of I_o from equation (2) into equation (1) we get,

The input resistance with feedback is given as

 

Ex. 9.9.4 Derive the expression for input resistance for a voltage shunt feedback amplifier.

Sol. : Step 1 : Draw the equivalent circuit current shunt amplifier.

The voltage shunt feedback topology is shown in Fig. 9.9.6 with amplifier input circuit is represented by Norton's equivalent circuit and output circuit represented by Thevenin's equivalent.

Step 2 : Obtain expression for l_s.

Applying KCL at input node we get,

Step 3 : Obtain expression for V_o in terms of I_i

The output current I is given as

 

Important Concept

R_m represents the open circuit transresistance without feedback and R_M is the transresistance without feedback taking the load R_L into account

Step 4 : Obtain expression for R_if .

Substituting value of VQ from equation (2) into equation (1) we get,

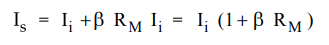
The input resistance with feedback Rif is given as

 

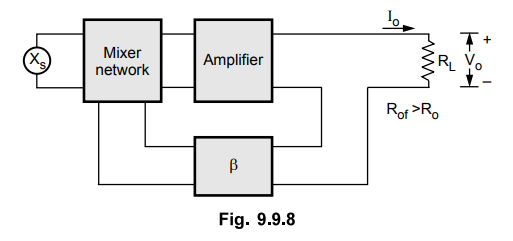
2. Output Resistance

• The negative feedback which samples the output voltage, regardless of how this output signal is returned to the input, tends to decrease the output resistance, as shown in the Fig. 9.9.7.

• On the other hand, the negative feedback which samples the output current, regardless of how this output signal is returned to the input, tends to increase the output resistance, as shown in the Fig. 9.9.8.

• Now, we see the effect of negative feedback on output resistance in different topologies (ways) of introducing negative feedback and obtain Rof quantitatively.

 

Ex. 9.9.5 Derive the expression for output resistance for a voltage series feedback amplifier.

AU : Dec.-16

Sol. : Step 1 : Draw the equivalent circuit.

In this topology, the output resistance can be measured by shorting the input source Vg = 0 and

looking into the output terminals with RL disconnected, as shown in the Fig. 9.9.9

 

Step 2 : Obtain expression for I in terms of V.

Applying KVL to the output side we get,

Substitutin the Vi from equation (2) min quation (1) we get, 

                     

Step 3 : Obtain expression for R_of.

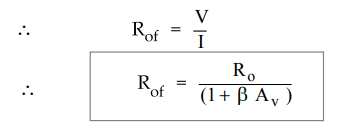
Important Concept

Here A_v is the open loop voltage gain without taking R_L in account.

Step 4 : Obtain expression for R’_of

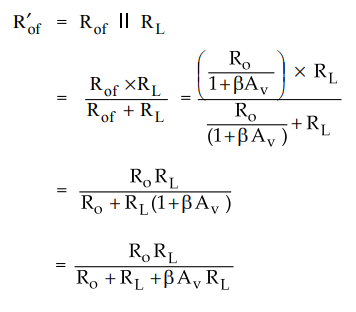
• Dividing numerator and denominator by (R_o + R_L) we get,

Important Concept

Here A_V is the open loop voltage gain taking R_L into account.

 

Ex. 9.9.6 Derive the expression for output resistance for a voltage shunt feedback amplifier.

AU : ECE : May-07

Sol. : Step 1 : Draw equivalent circuit.

In this topology, the output resistance can be measured by making Is = 0 and looking into the output terminals with RL disconnected, as shown in the Fig. 9.9.10.

Step 2 : Obtain expression for I in terms of V.

Applying KVL to the output side we get,

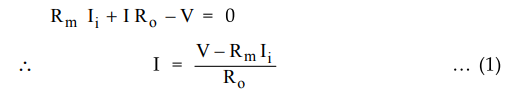
The input current is given as

I_i = -I_f - = - β V.   …. (2)

Substituting Ii from equation (2) in equation (1) we get,

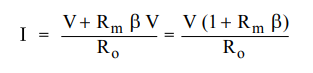
Step 3 : Obtain expression for R_of

Important Concept

Here, R_m is the open loop transresistance without taking R_L in account.

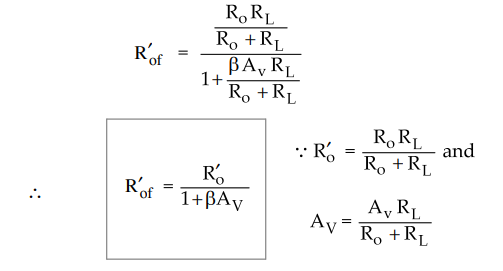
Step 4 : Obtain expression for R_of

Dividing numerator and denominator by (Ro + RL) we get,

Important Concept

Here A_V is the open loop voltage gain taking R_L into account.

 

Ex. 9.9.6 Derive the expression for output resistance for a voltage shunt feedback amplifier.

AU : ECE : May-07

Sol. : Step 1 : Draw equivalent circuit.

• In this topology, the output resistance can be measured by making Ig = 0 and looking into the output terminals with RL disconnected, as shown in the Fig. 9.9.10.

Step 2 : Obtain expression for I in terms of V.

Applying KVL to the output side we get,

Important Concept

Here, R_M is the open loop transresistance taking R_L in account.

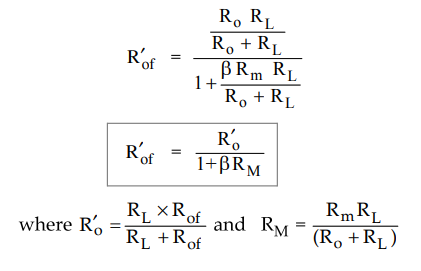
Step 4 : Obtain expression for R_of

Dividing numerator and denominator by (R_o + R_L) we get,

Important Concept

Here, AM is the open loop transresistance taking R_L into account.

 

Ex. 9.9.7 Derive the expression for output resistance for a current shunt feedback amplifier.

Sol. : Step 1 : Draw the equivalent circuit

• In this topology, the output resistance can be measured by open circuiting the input source Is = 0 and looking into the output terminals, with RL disconnected, as shown in the Fig. 9.9.11

Step 2 : Obtain expression for I in terms of V

Applying the KCL to the output node we get,

The input current is given as

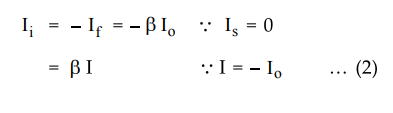
Substituting value of Ii from equation (2) in equation (1) we get,

Step 3 : Obtain expression for R_of

Important Concept

Here, A_i is the open loop current gain without taking R_L in account.

Here, Ai is the open loop tcurrent gain taking  RL in account.

 

Ex. 9.9.8 Derive the expression for output resistance for a current series feedback amplifier.

Sol. : Step 1 : Draw the equivalent circuit

• In this topology the output resistance can be measured by shorting the input source  V_s = 0 and looking into the output terminals with R_L disconnected, as shown in the Fig. 9.9.12.

Step 2 : Obtain expression for I in terms of V.

Applying KCL to the output node we get,

Important Concept

Here, G_m is the open loop transconductance without taking R_L in account.

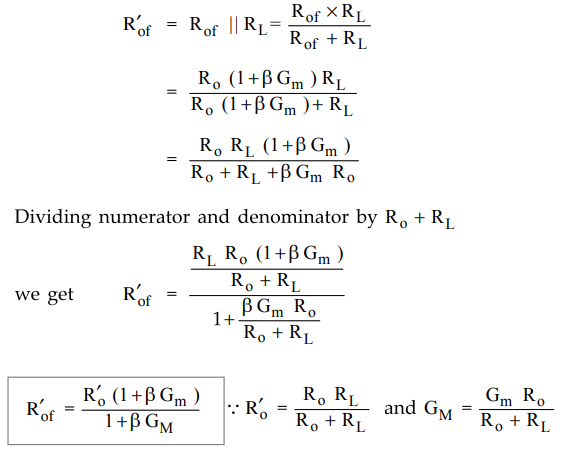
Important Concept

Note that here, G_M is the open loop current gain taking R_L in account.

Review Questions

1. Obtain the expression for output resistance for all four topologies.

AU : ECE : May-09, Marks 8

2. Derive the input impedance of a voltage series and current shunt.

AU : ECE : May-05, 06, Marks 8

3.Draw a block diagram of voltage shunt feedback amplifier and give its input resistance.

AU : ECE : May-07, Marks 2

4.Draw the block diagram of current series feedback and derive the expression for Ry

5. Mention the effect of negative feedback amplifier performance such as :

1) Gain 2) Input and output impedance 3) Sensitivity 4) Bandwidth.

Also explain the significance of the term (1 + XP) on the above performance parameters.

6. With a neat block diagram, explain the operation of following feedback amplifiers :

i) Voltage series feedback amplifiers ii) Current shunt feedback amplifier.

AU : May-17, Marks 13