Introduction to Bandpass Filters using Op-amp

Introduction to Bandpass Filters

A bandpass filter is basically a frequency selector. It allows one particular band of frequencies to pass. Thus, the pass band is between the two cut-off frequencies f_H and f_L where f_H > f_L. Any frequency outside this band gets attenuated. The frequency response of band pass filter is shown in Fig. 3.10.1.

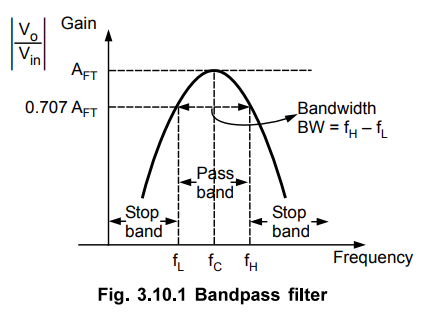
The pass band which is between f_H and f_L is called bandwidth of the filter denoted as BW.

BW = f_H - f_L  ….. (3.10.1)

The frequency at the centre of the pass band is called centre frequency denoted as f_C.

The gain is maximum at f_C and is denoted as A_FT called total passband gain.

Practically, the f_C is not exactly at the centre of the pass band hence, it is also called as resonant frequency. The gain at f_L and f_H is 0.707 A_FT.

There are two types of bandpass filters which are classified based on the figure of merit or quality factor (Q).

i) For Q < 10, the bandpass filter is called wide bandpass filter. In this type, the bandpass is wide and we get large bandwidth. The response is shown in the Fig. 3.10.2 (a).

ii) For Q > 10, the bandpass filter is called narrow bandpass filter. The bandpass is very narrow and the bandwidth is very small. Higher the value of Q, narrower is the passband and more selective is the filter. In the narrow band filter, the gain peaks at the centre frequency. The response is shown in Fig. 3.10.2 (b). 

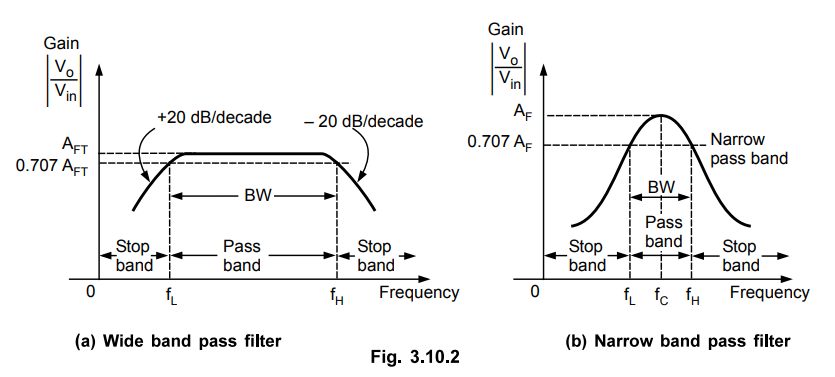
The gain roll off for f < f_L is + 20 dB/decade while f > f_H it is - 20 dB/decade.

For wide band pass filter, the centre frequency is given by,

f_C = √f_L f_H  … (3.10.2)

The relationship between Q and 3 dB bandwidth with fc is given by,

Q = f_C / B_W = F_C / f_H – f_L  … (3.10.3)

1. Wide Band Pass Filter

The wide band pass filter can be realised by simply cascading a high pass filter and low pass filter. If both high pass and low pass filters are of first order, the gain roll off in both the stop bands are ± 20 dB/decade and wide band pass filter is of first order. To get gain roll off ± 40 dB/decade and second order wide band pass filter, both high pass and low pass filters must be of second order and so on.

The Fig. 3.10.3 shows the first order wide band pass filter obtained by cascading first order high pass and low pass filter sections.

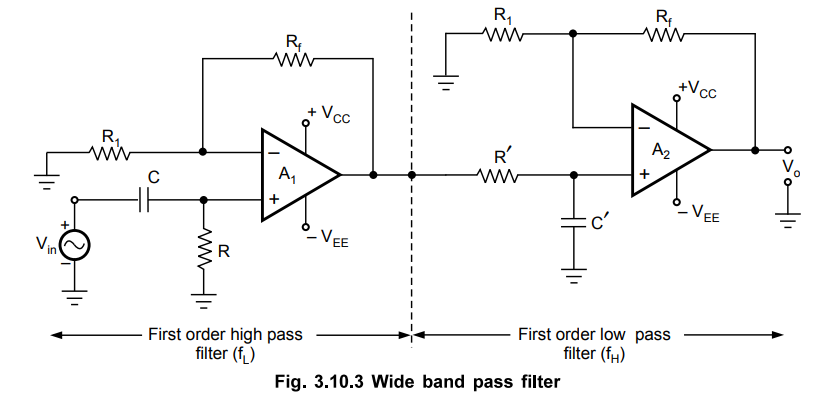
For wide band pass response, f_H must be greater than f_L. The voltage gain expressions for the two sections are reproduced here for the convenience.

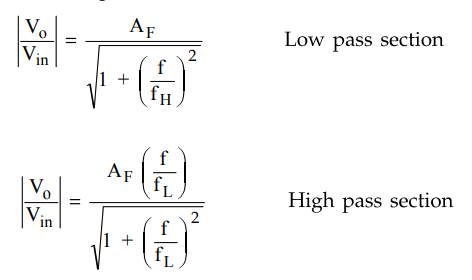
The design steps discussed earlier for first order low pass and high pass filters, are to be used to design the wide band pass filter of first order.

As the two circuits are in cascade, the overall gain of wide band pass filter is the product of the two gains expressed as,

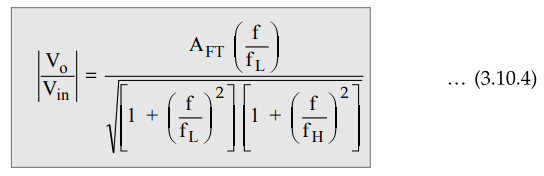
where  A_FT = Total pass band gain

f = Input frequency in Hz

f_L = Lower cut off frequency in Hz

f_H = Higher cut-off frequency in Hz

and  A_FT = A₁ A₂ …. (3.10.5)

where

A₁ = Gain of high pass section

A₂ = Gain of low pass section

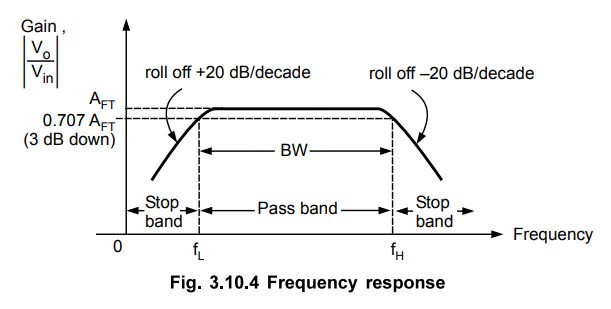
The frequency response for such a first order wide band pass filter is shown in the Fig. 3.10.4

2. Narrow Band Pass Filter

The narrow band pass filter uses only one op-amp as against two by wide band pass filter. It has following features :

i) It has two feedback paths.

ii) The op-amp is in the inverting configuration.

Due to the two feedback paths, it is called multiple feedback filter.

The Fig. 3.10.5 shows the circuit diagram of narrow band pass filter.

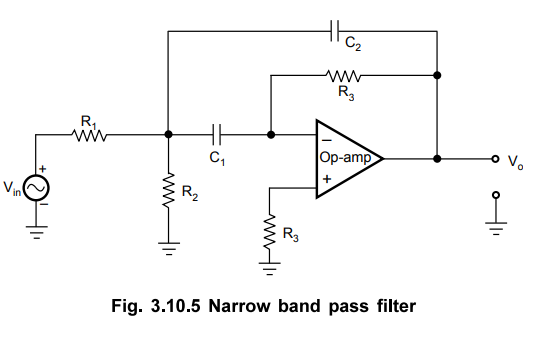
As seen from Fig. 3.10.5, the input is applied to the inverting input terminal. Thus, op-amp is in inverting configuration. The resistance R₃ connected to non-inverting input terminal is offset compensating resistance.        

The important parameters of the narrow band pass filter are f_L' f_H' the center frequency f_C' the gain at the center frequency AF and the quality factor Q.

The relationship of components with the various parameters are given by the following expressions.

Changing the centre frequency f_C :

Let     f_C = Original frequency

f_C = New centre frequency

The new centre frequency can be achieved by changing the resistance R₂. The new value of resistance say R₂, can be obtained as,

R₂ = R₂ (f_C / f_C )  ... (3.10.11)

This is an important advantage of the multiple feedback circuit, that f_C can be changed without changing gain A_F or bandwidth BW.

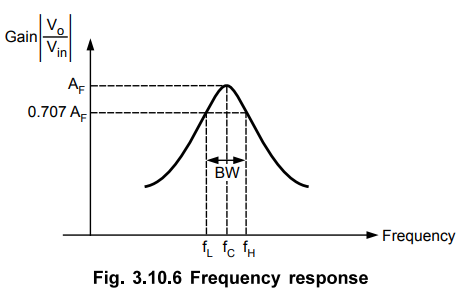
The frequency response of the narrow band pass filter is shown in Fig. 3.10.6.

Example 3.10.1 A bandpass filter has lower and upper cut-off frequencies of 300 Hz and 3000 Hz. Find the bandwidth and the resonant frequency.

May-05, Marks 6

Solution : f_L = 300 Hz,   f_H = 3000 Hz

The centre frequency f_C is also called resonant frequency.

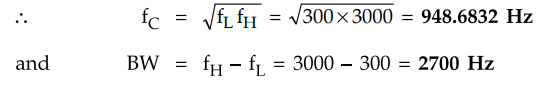
Example 3.10.2 Design a narrow band pass filter with fC = 3kHz,Q = 30,AF = 20. Assume C₁ = C₂ = C

Solution :

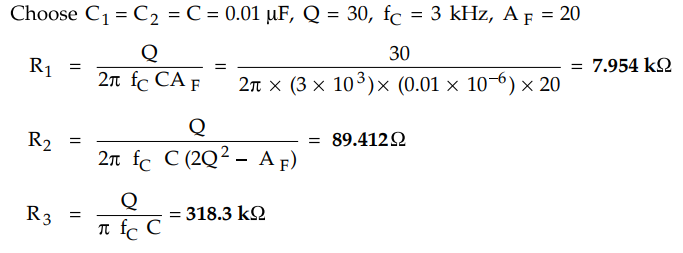
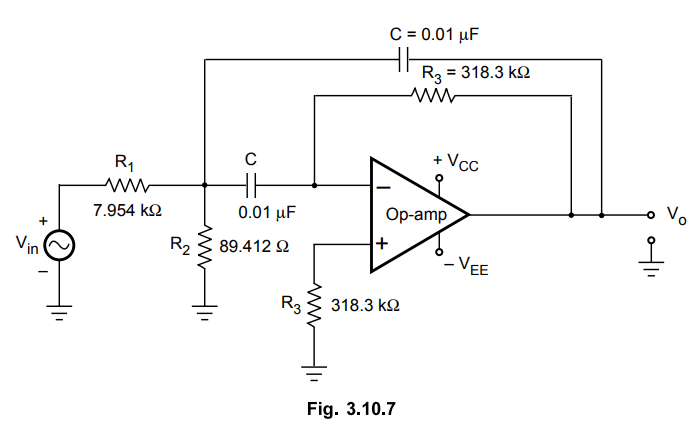
The designed circuit is shown in the Fig. 3.10.7

 Review Questions

1. What is band pass filter ? Which are the two types of band pass filters ?

2. Explain with neat diagram, the operation of wide band pass filter.

3. Explain with neat diagram, the operation of narrow band pass filter.

4. Design a wide band pass filter with f_L = 200 Hz and f_H =l kHz and a pass band gain = 4.

Draw the frequency response and calculate its Q value.

[ Ans.: Q = 0.56 ]