JFET Amplifiers

JFET Amplifiers

AU : May-03, 05, 09, 11, 14, Dec.-04, 05, 09

• In the second chapter, we described the operation of JFET, and analysed and designed the d.c. response of circuits containing JFET. In this chapter we emphasize the use of FETs in linear amplifier applications.

• JFET amplifiers provide an excellent voltage gain with the added advantages of a high input impedance. Because of their high input impedance and other characteristics JFETs are often preferred over BJTs for certain types of applications.

• Many of the concepts that relate to amplifiers using BJTs apply equally to FET amplifiers. There are three basic FET circuit configurations :

• Common source • Common drain and • Common gate 

• These are similar to the bipolar transistor common emitter, common collector and common base circuits, respectively. The only difference is that BJT controls a large output (collector) current by means of a relative small input (base current), whereas, FET controls an output (drain) current by means of small input (gate) voltage. It is important to note that in both the cases the output current is the controlled variable.

1. JFET as an Amplifier

• Field-effect transistor amplifier circuits use the voltage-controlled nature of the JFET. In the pin ch-off region, ID depends (approximately) only on V_GS

• Let us discuss the use of the JFET as an amplifier by considering the common-source circuit, shown in the Fig. 3.9.1.

• The voltage V_GG provides the necessary reverse-bias between gate and source of the JFET. The signal to be amplified is Vs. The V-I characteristics of the JFET is as shown in Fig. 3.9.2.

• On the output characteristics, a load line corresponding to VDD = 40 V and RD = 8 kQ is constructed. The transistor is biased at point Q and results in VDSQ = 20 V and IDQ = 2.70 mA.

• Assuming that the signal voltage Vs is a sinusoid of peak voltage Vm = 0.5 V, this signal is superimposed on the quiescent level. The instantaneous gate-to source voltage is

V_gs = V_s - V_GG

• The resulting waveforms for ID and VDS are as shown in Fig. 3.8.2.

• Both quantities, ID and VDS, can be considered as sinusoids superimposed on the d.c. values.

Then  V_GS = - V _GG + V_gs = -1.5 + 0.5 sin ωt

I_D = I_DQ + i_d = 2.70 + 0.5 sin ωt mA

V_out = V_DS = V_DSQ + V_dS = 20 +          4 sin ωt

• We observe that the output signal is greater than the input signal, thus indicating amplification.

• The magnitude of the voltage gain |Av | is the ratio of the output a.c. signal amplitude [4.0 V] to the input a.c. signal amplitude [0.5 V]. Then, in this example,

|A_V| = 4.0 / 0.5 = 8

• Note that the quiescent operating point Q is selected approximately at the midpoint of the load line. This gives undistorted output, i.e. output waveform is sinusoidal when the input signal is sinusoidal. If the operating point is selected either close to the ohmic region or near the pinch-off voltage, i.e. at the one of the ends of the load line, the output sinusoid would be clipped during either the positive or negative half-cycles of the input signal. In case of common-source circuit of JFET, there is a phase shift of 180° between the input and output sinusoidal voltages.

2. Small Signal A.C. Equivalent Circuit for JFET

• The JFET parameters are the major components of low frequency small signal model for JFET. We know that, drain to source current of JFET is controlled by gate to source voltage. The change in the drain current due to change in gate to source voltage can        be determined using the transconductance factor gm. It is given as

Δ I_d = gm Δ V_GS    ...(3.9.1)

• We know that, in BJT the relation between an output and input quantity is given by amplification factor P, whereas in JFET this relation is given by transconductance factor g _m.

• The another important parameter of JFET is drain resistance rd . It is given by

• It determines the output impedance Zo of the JFET amplifier.

• The amplification factor u of an FET is defined as

• The parameters gm, rd and u are related by,

µ = r_d g_m

JFET Low Frequency a.c. Equivalent Circuit

• Fig. 3.9.3 shows the small signal low frequency a.c. equivalent circuit for n-channel JFET. The relation of Id by Vgs is included as a current source gmVgs connected from drain to source. The input impedance is represented by the open circuit at its input terminals, since gate current IG is zero. The output impedance is represented by rd from drain to source.

Key Point : The lower case subscripts represent a.c. levels.

Approximate a.c Equivalent Circuit

• When the value of external drain resistance RD is very small as compared to the value of output impedance represented by rd, it is possible to replace rd by open circuit. This gives us approximate ac equivalent circuit of JFET amplifier, as shown in Fig. 3.9.4.

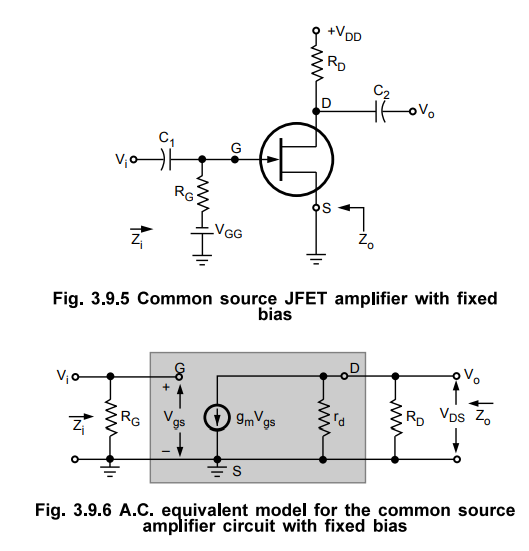
3. Common Source Amplifier with Fixed Bias

• Fig. 3.9.5 shows common source amplifier with fixed bias. The coupling capacitor Cx and C2 which are used to isolate the d.c. biasing from the applied ac signal act as short circuits for the ac analysis.

• Fig. 3.9.5 shows the low frequency equivalent model for the common source amplifier circuit with fixed bias. It is drawn by replacing :

• All capacitors and d.c. supply voltages with short circuits and

• JFET with its low frequency equivalent circuit.

• Now, we see the input impedance output impedance and voltage gain of the above model.

Input Impedance Z_i:

Looking into Fig. 3.9.5 we can say that,

Z_i = R_G ... (3.9.4)

Output Impedance Z_o:

• The output impedance Z_o is the impedance measured looking from the output side with input voltage (V_i) equal to 0. As V_i = 0,

V_gs = 0 and hence gm V_gs = 0

• The gm Vgs = 0 allows current source to be replaced by an open circuit, as shown in the Fig. 3.9.7.

Therefore the output impedance is,

Zo = R_D ||r_d  … (3.9.5)

• If the resistance r is sufficiently large compared to R_D, then we say that the output impedance is approximately equal to R_D.

Zo ≈ R_D     r_d  >> R_D … (3.9.6)

Voltage Gain Av :

Key Point : The negative sign in the equation for Av clearly indicates there is a phase shift of 180° between input and output voltages.

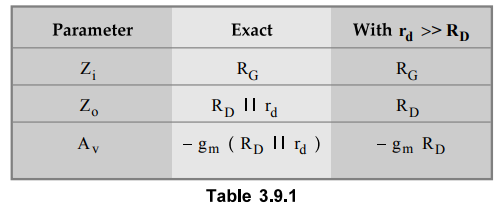
• Table 3.8.1 summarizes performance of common source amplifier with fixed bias.

Ex. 3.9.1 For the circuit shown in Fig. 3.9.8. Determine i)    Input impedance ii) Output impedance and iii) Voltage gain.

Sol. : i) We have,

Z_i = R_G = 1 MΩ 

ii) We have, Zo = rd ||RD = 50 K 115.1 K = 4628 Ω

iii) Voltage Gain Av : We have,

Av = -gm (rd ||RD )

= -2 mS (50 K 115.1 K)

= - 2 mS (4628) = - 9.256

Ex. 3.9.2 For the circuit shown in the Fig. 3.9.9 VGSQ = -2 V with IDSS = 8 mA and VP=-8V. Calculate gm, rd, Zir Zo and Ay. The value of Yos is given as 20 µS.

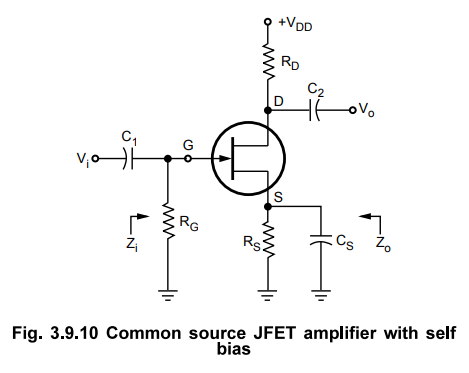
4. Common Source Amplifier with Self Bias (Bypassed Rs)

• Fig. 3.9.10 shows common source amplifier with self bias.

• The coupling capacitor C₁ and C₂ which are used to isolate the d.c. biasing from the applied a.c. signal act as short circuits for the low frequency analysis. Bypass capacitor Cs also acts as a short circuit for the low frequency analysis.

• Fig. 3.9.11 shows the low frequency equivalent model for the common source amplifier circuit with self bias. It is drawn by replacing

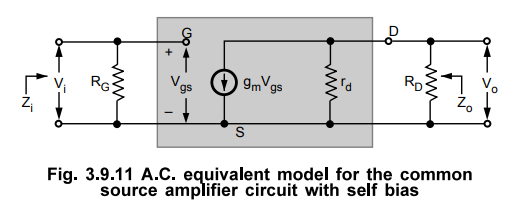
• All capacitors and d.c. supply V_DD with short circuits and,

• JFET with its low frequency equivalent circuit.

• Since the resulting low frequency equivalent circuit is same as a.c. equivalent circuit in Fig. 3.9.6, the equation for Z;, Zo and Av will also be same.

i) Input impedance Z_i :

Z_i = RG       ... (3.9.11)

ii) Output impedance Z_o :

Zo = rd||RD ...(3.9.12)

if rd >> R_D

Z_{o ≈} R_D        ... (3.9.13)

iii) Voltage gain A_v :

Av = -gm (rd ||RD )        ... (3.9.14)

If rd >> R D        

Av = “gm RD       ... (3.9.15)

• The negative sign in the equation (3.9.11) and (3.9.12) again indicates there is a phase shift of 180° between input and output voltages.