Joint distributions - marginal and conditional distributions

Joint distributions - marginal and conditional distributions.

 

1. Joint probability distribution

The probabilities of the two events A = {X ≤ x} and B = {Y ≤ y} defined as functions of x and y, respectively, are called probability distribution. functions.

Fx (x) = P(X ≤ x);

Fy (y) = P(Y ≤ y)

Note: We introduce a new concept to include the probability of the joint event {X ≤x, Y ≤y}.

 

2. Joint probability distribution of two random variables X and Y

We define the probability of the joint event {X ≤x, Y ≤y}, which is a function of the numbers x and y, by a joint probability distribution function and denote it by the symbol Fx, y (x, y). Hence

Fx, y (x,y) = p {X ≤ x, Y ≤ y}

Note: Subscripts are used to indicate the random variables in the bivariate probability distribution. Just as the probability mass function of a single random variable X is assumed to be zero at all values outside the range of X, so the joint probability mass function of X and Y is assumed to be zero at values for which a probability is not specified.

 

3. Properties of the joint distribution

A joint distribution function for two random variables X and Y h several properties.

 

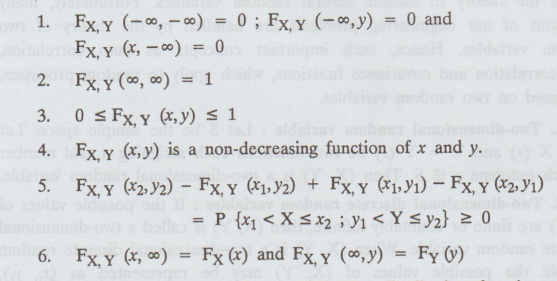
4. Joint probability function of the discrete random variables X and Y

If (X, Y) is a two-dimensional discrete random variable such that f(x_i, y_j) = P(X = x_i, Y = y_j) = P_ij is called the joint probability function or joint probability mass function of (X, Y) provided the following conditions are satisfied.

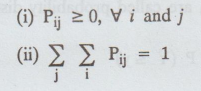
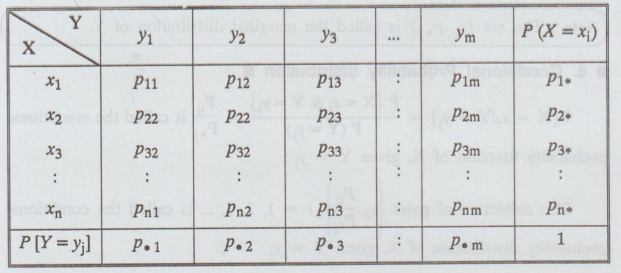
The set of triples {xi, yj, Pij), i = 1, 2, ... n, j = 1, 2, ... m is called the joint probability distribution of (X, Y). It can be represented in the form of table as given below.

 

5. Marginal probability distribution

If more than one random variable is defined in a random experiment, it is important to distinguish between the joint probability distribution of X and Y and the probability distribution of each variable individually. The individual probability distribution of a random variable is referred to as its marginal probability distribution.

In general, the marginal probability distribution of X can be determined from the joint probability distribution of X and other random variables.

 

6. Marginal probability mass function of X

If the joint probability distribution of two random variables X and Y is given, then the marginal probability function of X is given by

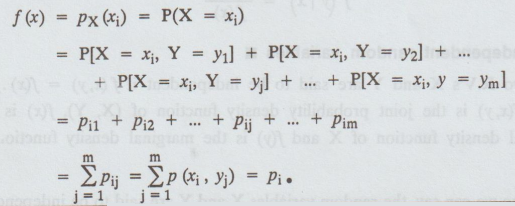
Note: The set {x_i, P_i.} is called the marginal distribution of X.

 

7. Marginal Probability mass function of Y

If the joint probability distribution of two random variables X and Y is given, then the marginal probability function of Y is given by

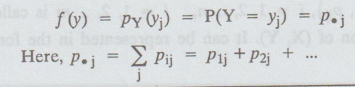
Note: The set {y_i, P.j} is called the marginal distribution of Y.

 

8. Conditional Probability distribution

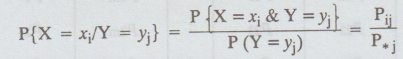 is called the conditional probability function of X, given Y = y_j

The collection of pairs {xi, p_ij/p_i} i = 1, 2, 3, ... is called the conditional probability distribution of X, given Y = y_j

Similarly, the collection of pairs, {yi, p_ij/p_i} , j = 1, 2, 3, ... is called the conditional probability distribution of Y given X = x_i.

let (X, Y) be the two dimensional continuous R.V. The conditional probability density function of X given Y is denoted by f (x | y) and is defined as,

f(x | y) = f(x, y) / f (y)

Similarly, the conditional probability density function of Y given X is denoted by f ( y | x) and is defined as,

f(y | x) = f(x, y) / f(x)

 

9. Independent random variables

Two R.V's X and Y are said to be independent if f (x, y) = f(x).flv) where f(x,y) is the joint probability density function of (X, Y), f(x) is the marginal density function of X and f(y) is the marginal density function of Y.

Also we can say, the random variables X and Y are said to be independent R.V's if

P_ij = P_i* × P_*j

where Pij is the joint probability function of (X, Y), P _i* is the marginal probability function of X and P_*j  is the marginal probability function of Y.

 

10. Joint probability density function

If (X, Y) is a two-dimensional continuous R.V such that

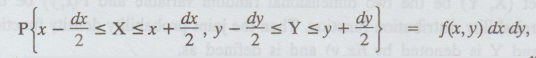
then f(x, y) is called the joint p.d.f. of (X, Y), provided f(x, y) satisfies the following conditions.

(i) f(x, y) ≥ 0, ∀ (x, y) ∈ R, where 'R' is the range space.

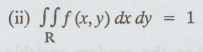
Moreover, if D is a subspace of the range space R,

P{(X, Y) E D} is defined as,

 

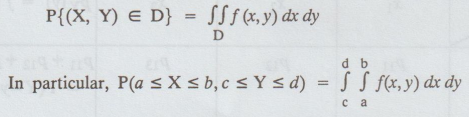
11. Cumulative distribution function

If (X, Y) is a two-dimensional continuous random variable, then F(x, y) = P(X ≤ x and Y ≤ y) is called the cdf of (X, Y) and is defined as,

 

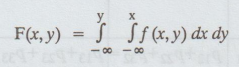
12. Marginal density function

If (X, Y) is a two-dimensional continuous random variable, then

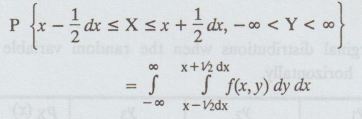
Let (X, Y) be the two dimensional random variable. Then, the marginal probability density function of X is denoted by f(x) and is defined as,

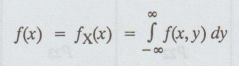
Similarly, the marginal probability density function of Y is denoted by f(y) and is defined as,

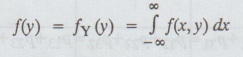
13. Joint probability density function

Let (X, Y) be the two dimensional random variable and F(x, y) be the joint probability distribution function. Then the joint probability density function of X and Y is denoted by f(x, y) and is defined as,

f(x, y) = ∂²F(x,y) / ∂x ∂y

 

14. Table I.

To calculate marginal distributions when the random variable X takes horizontal values and Y takes vertical values.

 

15. Table - II

To calculate marginal distributions when the random variable X takes vertically and Y takes horizontally.