Kirchoff's laws

KIRCHOFF'S LAWS

Kirchoff's laws help us to solve the electrical networks. There are two laws which are stated as below.

1. Kirchoff's current law (Point law or first law)

It states that, "the algebraic sum of the currents meeting at a junction (node) is equal to zero."

Explanation:

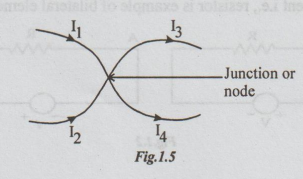
Let the currents I₁, I₂, I₃ and I₄ flow through the conductors meeting at a junction as shown. Take the currents flowing towards the junction as positive and those flowing away from junction as negative.

Then, according to the above statement,

I₁ + I₂ - I₃ - I₄ = 0

⇒ I₁ + I₂ = I₃ + I₄

i.e., At a junction, the sum of incoming currents = The sum of outgoing currents. This is other way of stating the Kirchoff's law.

Note: In case of A.C. circuits, Kirchoff's current law, states that the phasor sum of incoming currents is equal to the phasor sum of outgoing currents.

2. Kirchoff's Voltage Law: (Second law or mesh law)

"The algebraic sum of electromotive forces plus the algebraic sum of voltages across the impedances, in any closed electrical circuit is equal to zero."

Mathematically, Σ emf + Σ IZ =0, in any closed electrical circuit.

The reader may notice that we have to take algebraic sum of electromotive forces and algebraic sum of voltages across impedances. It may be either positive or negative. The following rules determine the sign for electromotive force and also for voltage drop across impedance.

To determine the sign of electromotive force

Let us traverse round the loop in a clockwise direction. If we reach negative terminal first and then positive terminal, that voltage is called voltage rise. If we reach first positive terminal and then negative terminal, it is called voltage fall.

Voltage rise is given positive sign and voltage fall is given negative sign. The reader need not try to know at present what voltage rise is and voltage fall. He can remember the following rule.

While traversing round a closed circuit, if he leaves a voltage source at positive, it must be given positive sign. If he leaves the voltage source at negative, it must be given negative sign.

For this, the polarity of the leaving terminal is important.

To determine the sign of voltage across the impedance

If the direction of current through an impedance and direction of traversing round the loop are same, the voltage drop is taken as negative.

If the direction of current through the impedance is opposite to that of traversing round the loop, then the voltage across the impedance is taken as positive.

Note:

1.Till the reader gets familiarity, he is advised to follow the above rule for sign convention.

2.In the statements given for the Kirchoff's laws, the right side of the equation is zero.

3. We can traverse round the circuit in anti-clockwise direction also, for applying KVL. Even for that, the determination of sign can be as stated above.

4. The determination of sign may be given in various ways. The reader is advised not to get confusion. He can proceed confidently in one method.

5. In these methods, the directions of currents for different branches can be given by random. Then, the laws are applied to get the equations.

6. On solving the equations, if all currents are found to be positive values, then given directions are correct. If a particular current is found to be negative, the direction of that current alone will be reversed. There is no change of magnitude.

Explanation: Consider the circuit shown in the figure.

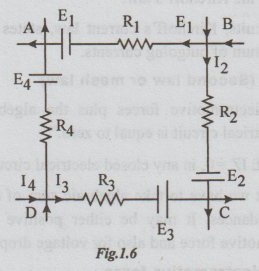
ABCDA is one of the closed paths of the given circuit. AB, BC, CD and DA are the branches. We assume that I₁, I₂, I₃ and I₄ are the branch currents. The directions of these currents are given by random, independent of the polarities of the source.

At the nodes A, B, C and D there are some more live conductors.

Let us apply KVL for the loop ABCDA. We start from A, go clockwise and come back to A at last. We know that,

Σ emf + Σ IR = 0

Applying sign convention, we get

Σ emf = -E₁ + E₂ + E₃ + E₄

Σ IR =I₁ R₁ - I₂ R₂ - I₃ R₃ - I₄ R₄

Therefore, the equation becomes,

(-E₁ + E₂ + E₃ + E₄ ) + (I₁ R₁ - I₂ R₂ - I₃ R₃ - I₄ R₄) = 0 ... (i)

Note: (i) If we traverse in the anticlockwise direction, for the loop ADCBA. Applying KVL, we get,

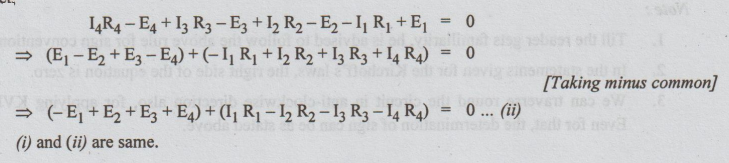
i.e., We can state that whether the circuit is traversed round either clockwise or anti-clockwise, we get the same equation.

2. The student should not traverse in one direction, say clockwise to determine the sign of emf and another direction anti-clockwise to determine the sign of IR, for any particular closed path.

Methods of solving electrical network by Branch Current Method

Step 1: Identify the nodes or junctions and hence the branches. Assume the direction of current in a branch randomly.

Step 2: Apply KCL at the nodes.

Step 3: Apply KVL for the closed paths.

Step 4: Write the equations.

Step 5: Obtain the unknown currents by solving the equations.