Loop (mesh) current method

 LOOP (MESH) CURRENT METHOD

In the loop current method, we need to write (and solve) equations for as many currents as the number of independent loops. The number of independent loops is equal to (b − n + 1).

This is based on Kirchoff's voltage law and applicable to only planar networks. Here KCL is applied automatically. In this method the loop current is an independent variable. The number of loop current equations is equal to number of independent loops.

Consider the network shown below. For convenience numerical are not given.

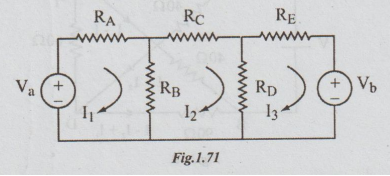
In the network given, there are three nodes (junctions) i.e., n = 3. The branches are five i.e., b = 5. If/= number of independent loops, l = b – n + 1 = 5 – 3 + 1 = 3.

Therefore, there will be three independent loop equations.

Assume, the loop currents to be I₁, I₂ andI₃ as shown in the figure, all clockwise.

Each loop current is confined to that particular loop only. The currents through R_A, R_C, R_E are I₁, I₂, I₃ respectively.

The current through R_B is I₁ - I₂, and through R_D is I₂ - I₃. Applying KVL to the left loop, we get

It is usual to write these equations in terms of self and mutual resistances (impedances). The self resistance of a loop is the sum of the resistances encountered in a traverse of that loop. Thus for the circuit drawn,

the self resistance of loop 1 = R₁₁ = R_A + R_B

the self resistance of loop 2 = R₂ = R_B+ R_C + R_D

the self resistance of loop 3 = R₃₃ = R_D + R_E

The resistance which is common to more than one loop is called mutual resistance. Denoting the mutual resistance between loop 1 and loop 2 by R₁₂ and so on.

 R₁₂ = R₂₁ = R_B

R₂₃ = R₃₂ = R_D

Introducing these in the set of loop equations (1), (2) & (3).

R₁₁I₁ - R₁₂I₂ = V_a...(4)

-R₂₁ I₁ - R₂₂ I₂ - R₂₃ I₃ = V_a ....(5)

And

- R₃₂ I₂ + R₃₃ I₃ =- V_b ....(6)

It should be noted that all the terms representing mutual resistances have a negative sign. This can be avoided by putting R₁₂ = R₂₁ - R_B.

Finally the general form of loop equations for the given circuit containing three independent loops will be

R₁₁ I₁ + R₁₂ I₂ + R₁₃ I₃ = V_a ...(7)

R₂₁ I₁ + R₂₂ I₂ + R₂₃ I₃ = 0 ...(8)

R₃₁ I₁ + R₃₂ I₂ + R₃₃ I₃ = V_b ...(9)

Writing equations (7), (8), (9) in the matrix form, we get

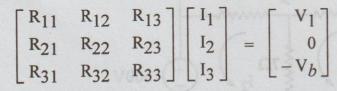
In general the above matrix form is expressed as below:

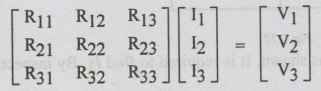
The last general form is to be remembered well for solving the problems.

Here, V₁= the algebraic sum of the e.m.f. in the loop 1.

V₂ = the algebraic sum of the e.m.f. in the loop 2.

Similarly, V₃ = the algebraic sum of the e.m.f. in loop 3. An e.m.f. is assigned positive if the loop current leaves at positive terminal of the source. For example, in loop 1, V₁ =+ V_a. I₃ leaves Vь at negative terminal. So, V₃ = - V_b.

[Note:

1. If directions of loop currents are not given assume all of them to be clockwise blindly. After solving, if a particular loop current is found to be negative, reverse only the direction of that loop current.

2. The self resistances are always taken as positive.

3. The mutual resistance is positive if the current through it is the sum of two loop currents.

 4. The mutual resistance is negative if the current through it is the difference of two loop currents.

5. From the matrix, we can find the various loop currents by using determinants. Remember,

I₁ = Δ₁/Δ ,I₂ = Δ₂ /Δ ,I₃ = Δ₃/Δ

The students will commit mistakes generally by taking I₁ = Δ/Δ₁ ,I₂ = Δ/Δ₂ and so on.

6. Loop current method can also be used for AC circuits. There, you have to replace R by Z.

7. If the network consists of practical current source it is convenient to convert it into practical voltage source, for loop current analysis.