M.M.F. Method of Determining Regulation

M.M.F. Method of Determining Regulation AU : May-13, 17,18, Dec.-15, 16, 17

This method of determining the regulation of an alternator is also called Ampere-turn method or Rothert's M.M.F. method. The method is based on the results of open circuit test and short circuit test on an alternator.

For any synchronous generator i.e. alternator, it requires M.M.F. which is product of field current and turns of field winding for two separate purposes.

1. It must have an M.M.F. necessary to induce the rated terminal voltage on open circuit.

2. It must have an M.M.F. equal and opposite to that of armature reaction m.m.f.

Key Point : In most of the cases as number of turns on the field winding is not known, the M.M.F. is calculated and expressed in terms of the field current itself.

The field M.M.F. required to induce the rated terminal voltage on open circuit can be obtained from open circuit test results and open circuit characteristics. This is denoted as F_O 

We know that the synchronous impedance has two components, armature resistance and synchronous reactance. Now synchronous reactance also has two components, armature leakage reactance and armature reaction reactance. In short circuit test, field M.M.F. is necessary to overcome drop across armature resistance and leakage reactance and also to overcome effect of armature reaction. But drop across armature resistance and leakage reactance is very small and can be neglected. Thus in short circuit test, field M.M.F. circulates the full load current balancing the armature reaction effect. The value of ampere-turns required to circulate full load current can be obtained from short circuit characteristics. This is denoted as F_AR.

Under short circuit condition as resistance and leakage reactance of armature do not play any significant role, the armature reaction reactance is dominating and hence the power factor of such purely reactive circuit is zero lagging. Hence F^ gives demagnetising ampere turns. Thus the field M.M.F. is entirely used to overcome the armature reaction which is wholly demagnetising in nature.

The two components of total field M.M.F. which are Fo and F, Circuit Characteristics) and S.C.C. (Short Circuit Characteristics) as shown in the Fig. 2.14.1.

If the alternator is supplying full load, then total field M.M.F. is the vector sum ofits two components F_O and FAR- This depends on the power factor of the load which alternator is supplying. The resultant field M.M.F. is denoted as FR. Let us consider the various power factors and the resultant F_R.

Zero lagging p.f. : As long as the power factor is zero lagging, the armature reaction is completely demagnetising. Hence the resultant FR is the algebraic sum of the two components F_O and F_AR. Field M.M.F. is not only required to produce rated terminal voltage but also required to overcome completely demagnetising armature reaction effect.

This is shown in the Fig. 2.14.2.

OA = Fo    

AB = F_AR Demagnetising        

OB = F_R = F_O + F_AR

Total field M.M.F. is greater than F_O.

Zero leading p.f. : When the power factor is zero leading then the armature reaction is totally magnetising and helps main flux to induce rated terminal voltage. Hence net field M.M.F. required is less than that required to induce rated voltage normally, as part of its function is done by magnetising armature reaction component. The net field M.M.F. is the algebraic difference between the two components F_O and F_AR. This is shown in the Fig. 2.14.3

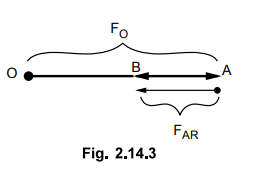
OA = F_O

AB = F_AR Magnetising

OB = F_O - FAR = FR

Total M.M.F. is less than F_O

Unity p.f. : Under unity power factor condition, the armature reaction is cross magnetising and its effect is to distort the main flux. Thus F_O and F^ are at right angles to each other and hence resultant M.M.F. is the vector sum of F_O and F_AR. This is shown in the Fig. 2.14.4.

OA = F_O

AB = FAR Cross magnetising

General Case : Now consider that the load power factor is cos . In such case, the resultant M.M.F. is to be determined by vector addition of F_O and F_AR.

Cos ϕ , lagging p.f. : When the load p.f. is cos lagging, the phase current Iaph lags Vph by angle . The component F_O is at right angles to V_ph while F_AR is in phase with the current I_aph. This is because the armature current Iaph decides the armature reaction. The armature reaction FAR due to current Iaph is to be overcome by field M.M.F. Hence while finding resultant field M.M. F-/ - F_AR should be added to F_O vectorially. This is because resultant field M.M.F. tries to counterbalance armature reaction to produce rated terminal voltage. The phasor diagram is shown in the Fig. 2.14.5. 

From the phasor diagram the various magnitudes are,

OA = F_O,

AB = F_AR' OB = F_R

Consider triangle OCB which is right angle triangle. The F_AR is split into two parts as,

AC = F_AR

sin ϕ and BC = F_AR cos ϕ

(F_R)² = (F_O + F_AR sin ϕ)² + (F_AR cos ϕ)² … (2.14.1)

From this relation (2.14.1), FR can be determined.

Cos ϕ J leading p.f. : When the load p.f. is cos ϕ leading, the phase current I_aph leads V_ph by ϕ • The component F_O is at right angles to V_ph and F_AR is in phase with I_aph. The resultant F_AR can be obtained by adding - F_AR to F_O. The phasor diagram is shown in the Fig. 2.14.6.

From the phasor diagram, various magnitudes are,

AC = F_AR sin ϕ and

BC = F_AR COS ϕ

OA = F_O, AB = F_AR and OB = F_R

Consider triangle OCB which is right angle triangle.

(OB)² = (OC)2 + (BC)²

(FR)² = (Fo - F_AR sin ϕ) ² + (F_AR cos ϕ)² …(2.14.2)

From the relation (2.14.2), F_R can be obtained.

Using relations (2.14.1) and (2.14.2), resultant field M.M.F. F_R for any p.f. load condition can be obtained. 

Once F_R is known, obtain corresponding voltage which is induced e.m.f. E_ph, required to get rated terminal voltage V_ph. This is possible from open circuit characteristics drawn.

Once E_ph is known then the regulation can be obtained as,

% Reg. = E_ph - V_ph / V_ph × 100

Note : To obtain E_ph corresponding to F_R, O.C.C. must be drawn to the scale, from the open circuit test readings.

Key Point : This ampere-turn method gives the regulation of an alternator which is lower than that actually observed. Hence the method is called optimistic method.

Important note : When the armature resistance is neglected then Fo is field m.m.f. required to produce rated V_ph at the output terminals. But if the effective armature resistance R_aph is given then Fo is to be calculated from O.C.C. such that Fo represents the excitation (field current) required to produce a voltage of V_ph + I_aph R_a cos ϕ

where          V_ph = Rated voltage per phase

I_aph = Full load current per phase

R_a = Armature resistance per phase

cos ϕ = Power factor of the load

It can also be noted that, F_R can be obtained using the cosine rule to the triangle formed by F_O, F_AR and F_O as shown in the Fig. 2.14.8. 

Using cosine rule to triangle OAB,

(F_R)² = (F_O) ² + (F_AR) ² - 2 F_O F_AR COS (F_O ^Λ F_AR)

F_O ^Λ F_AR = 90 + ϕ if ϕ is lagging

= 90 - ϕ if is leading

Students can use equations (2.14.1), (2.14.2) or (2.14.3) to calculate F_R.

The angle between E_O and V_ph is denoted as 8 and is called power angle.

Neglecting R_a we can write,

I_aX_s cos ϕ = E_O sin δ

P_d = V_phI_a cos ϕ = Internal power of machine

P_d = V_ph ( E_O / X_S ) sin δ

Key Point This equation shows that the internal power of the machine is proportional to sin δ.

 

Example 2.14.1 The open and short circuit test readings for a 3 phase star connected, 1000 kVA, 2000 V, 50 Hz synchronous generator are

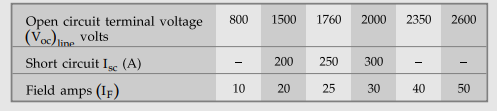
The armature effective resistance is 0.2 Ω per phase. Draw the characteristics curves and estimate full load percentage regulation (a) 0.8 p.f. lagging (b) 0.8 p.f. leading. Use M.M.F. method. AU : May-17, Dec.-15, Marks 16

Solution : While sketching O.C.C., convert the given line values to phase by dividing each value by √3. This is because the alternator is star connected. The characteristics are shown in Fig. 2.14.11.

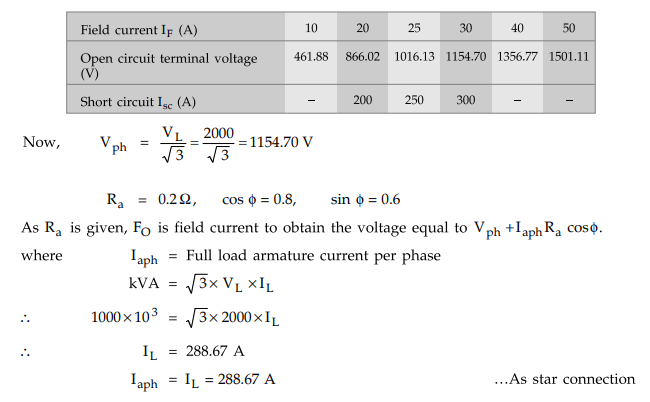
Vph + Iph Ra cos ϕ = 1154.70 + (288.67) (0.2) (0.8) = 1200.8872 volts

Find F_O corresponding to voltage of 1200.88 V from O.C.C

So F_O = 32.5 A

While FAR is field current required to circulate full load short circuit current of 288.67 so obtain it from S.C.C.

F_AR - 29.5 A

For lagging power factor the phasor diagram is shown in Fig. 2.14.9.

From triangle OCB,

(FR)² - (F_O + F_AR sin ϕ)² + (FAR cos ϕ)²

= (32.5 + 29.5 × 0.6)² + (29.5 × 0.8)² = (2520.04) + (556.96)

= 3077

F_R = 55.47 A

Now obtain E_ph corresponding to F_R = 55.47 A of field current from O.C.C. For F_R = 55.47, E_ph = 1560 V from graph shown in the Fig. 2.14.11.

For 0.8 p.f. leading, F_R can be obtained as follows,

cos ϕ = 0.8, ϕ = 36.86° 

90 - ϕ = 90 - 36.86 = 53.14°

Using cosine rule to triangle OAB

 

Example 2.14.2 A 1.1 MVA, 2.2 kV, 3 phase, star - connected alternator gave the following test result during OC and SC tests :

The effective resistance of the 3 - phase winding is 0.22 Ω /ph. Estimate the full - load voltage regulation at 0.8 pf. lagging. 

i) By Synchronous impedance method and ii) Ampere – turn method

Solution :

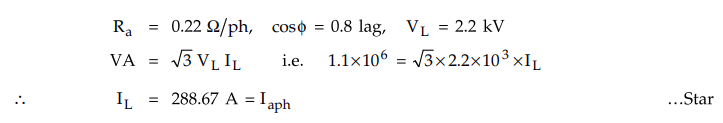
Plot O.C.C. and S.C.C. on graph. Convert the open circuit voltage values to phase values while sketching O.C.C., by dividing each value by √3 as alternator is star connected. The graphs are shown in the Fig.2.14.12

i) Synchronous impedance method

ii) Ampere - turn method :

As R_a is given, F_O is the field current to obtain the voltage equal to V_ph + I_aph-R_a cos ϕ

V_ph + I_aph R_a cos ϕ = 1270.17 + 288.67 × D.22 × 0.8 = 1320.97 V

From O.C.C. in    Fig .2.14.12, I_f corresponding to 1320.97 V is F_O = 32.5 A.

While F_AR is I_f required to circulate full load short circuit current of 288.67 A i.e. F_AR = 14 A

Consider the phasor diagram for 0.8 lagging p.f. as shown in the Fig. 2.14.13. From the Fig. 2.14.13,

(FR)² = (F_O + F_ARsin ϕ) ² + (FAR cos ϕ) ² = (32.5 + 14 × 0.6)² + (14 × 0.8)²

F_R = 42.4 A

From O.C.C. in the graph, E_ph corresponding to F_R = I_f = 42.4 A is 1520 V. 

 

Example 2.14.3 A 3.3 kV alternator gave the following results :

A field current of 18 A is found to cause the full load current to flow through the winding during short circuit test. Predetermine the full load voltage regulation at (1) 0.8 pf lag and (2) 0.8 pf lead by MMF method. AU : May-13, Marks 8

Solution : The field current required for producing rated terminal voltage of 3.3 kV is 37.5 A i.e. F_O = 37.5 A. The field current required to circulate full load current during short circuit is 18 A i.e. F_AR = 18 A

Vph = 3.3 kV / √3 = 1905.2558 V

73

i) cos ϕ = 0.8 lagging : The phasor diagram is shown in the Fig. 2.14.14 (a).

(F_R)² = (F_O + F_AR sin ϕ)² + ( F_AR cos ϕ)² = (37.5 + 18 × 0.6)² + (18 × 0.8)²

i.e. F_R = 50.4 A

Alternative method to obtain F_R is to use consine rule to triangle OAB.

To find E_ph corresponding to F_R, plot open circuit characteristics to the scale from given table as shown in the Fig. 2.14.14 (b). Note that phase values are obtained by dividing the given voltages by √3 and are used to obtain the graph.

 

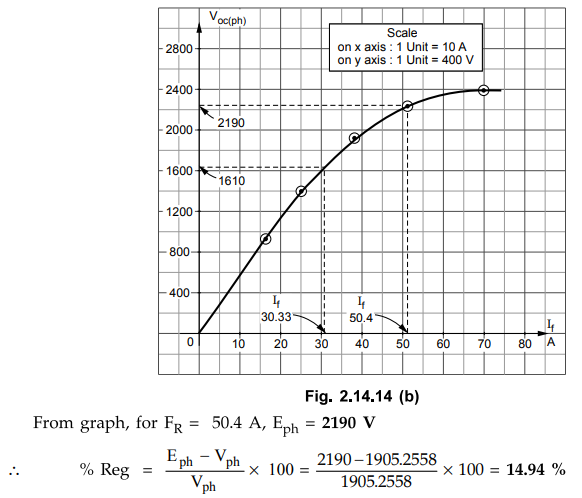
 ii) cos ϕ = 0.8 leading

The phasor diagram is shown in the Fig. 2.14.14(c).

 

Examples for Practice

 Example 2.14.4 The following test results are obtained on 6600 V, alternator,

A field current of 20 A is found necessary to circulate full load current on short circuit of the armature. Calculate by a) mmf method and b) The synchronous impedance method, the full load regulation of 0.8 p.f. (lagging). Neglect resistance and leakage reactance.

[Ans.: - 21.27 %, -19.71 %]

Example 2.14.5 A 3 phase, 200 kVA, 1.1 kV, 50 Hz star connected alternator having an effective per phase resistance of 0.62 Ω, gave the following results

Using MMF method, find the voltage regulation at 100 A, at a) 0.8 lagging and b) 0.8 leading p.f.

[Ans.: 104.38 % 73.205 %]

Example 2.14.6 A 1 MVA, 11 kV, 3- ϕ, star connected synchronous machine has the following OCC test data,

where E_OL is line to line voltage at no load. The short circuit test yielded full load current at a field current of 65 A, the armature resistance is negligible, Calculate the voltage regulation at full load 0.866 p.f. lagging by m.m.f. method.

[Ans.: 22.031 %]

Review Question

1. Explain M.M.F. method cf predeterming the regulation of alternator.