Electromagnetic Theory: Unit III: (b) Magnetic Forces, Magnetic Materials and Inductance
Magnetic Boundary Conditions
with Example Solved Problems
• The conditions of the magnetic field existing at the boundary of the two media when the magnetic field passes from one medium to other are called boundary conditions for magnetic fields or simply magnetic boundary conditions.
Magnetic Boundary Conditions
AU
: Dec.-04, 11, 14, 17, May-17
•
The conditions of the magnetic field existing at the boundary of the two media
when the magnetic field passes from one medium to other are called boundary
conditions for magnetic fields or simply magnetic boundary conditions. When we
consider magnetic boundary conditions, the conditions of 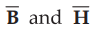 are
studied at the boundary. The boundary between the two different magnetic
materials is considered. To study conditions of
are
studied at the boundary. The boundary between the two different magnetic
materials is considered. To study conditions of 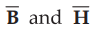 at the boundary,
both the vectors are resolved into two components ;
at the boundary,
both the vectors are resolved into two components ;
a)
Tangential to boundary and
b)
Normal (perpendicular) to boundary.
•
Consider a boundary between two isotropic, homogeneous linear materials with
different permeabilities µ1 and µ2 as shown in the Fig.
8.8.1. To determine the boundary conditions, let us use the closed path and the
Gaussian surface.

1. Boundary Conditions for Normal Component
•
To find the normal component of ![]() , select a closed Gaussian surface in the form of a right
circular cylinder as shown in the Fig. 8.8.1. Let the height of the cylinder be
Ah and be placed in such a way that Δh/2 is m medium 1 and remaining Δh/2 is in
medium 2. Also the axis of the cylinder is in the normal direction to the
surface.
, select a closed Gaussian surface in the form of a right
circular cylinder as shown in the Fig. 8.8.1. Let the height of the cylinder be
Ah and be placed in such a way that Δh/2 is m medium 1 and remaining Δh/2 is in
medium 2. Also the axis of the cylinder is in the normal direction to the
surface.
•
According to the Gauss's law for the magnetic field,
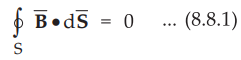
•
The surface integral must be evaluated over three surfaces,
i)
Top, ii) Bottom and iii) Lateral.
•
Let the area of the top and bottom is same, equal to ΔS.
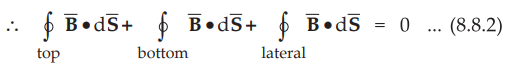
•
As we are very much interested in the boundary conditions, reduce Δh to zero.
As Δh → 0, the cylinder tends to boundary
and only top and bottom surfaces contribute in the surface integral. Thus
surface integrals are calculated for top and bottom surfaces only. These
surfaces are very small. Let the magnitude of normal component of ![]() be
BN1 and BN2 in medium 1 and medium 2 respectively. As
both the surfaces are very small, we can assume B N1 and B N2
constant over their surfaces. Hence we can write,
be
BN1 and BN2 in medium 1 and medium 2 respectively. As
both the surfaces are very small, we can assume B N1 and B N2
constant over their surfaces. Hence we can write,
For
top surfaces

•
Note that the negative sign is used for one of the surface integrals because
normal component in medium 2 is entering the surface while in medium 1 the
component is leaving the surface. Hence B N1 and B N2 are
in opposite direction.
•
From equation (8.8.6), we can write,
B
N1 ΔS = B N2 ΔS
i.e.
B N1 = B N2 ...
(8.8.7)
•
Thus the normal component of ![]() is continuous at the boundary.
is continuous at the boundary.
•
As the magnetic flux density and the magnetic field intensity are related by,
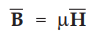
•
Thus equation (8.8.7) can be written as,
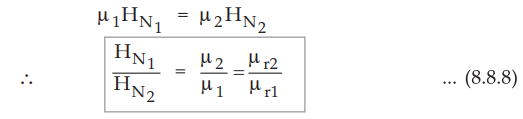
•
Hence the normal component of ![]() is not continuous at the boundary. The
field strengths in two media are inversely proportional to their relative
permeabilities.
is not continuous at the boundary. The
field strengths in two media are inversely proportional to their relative
permeabilities.
2. Boundary Conditions for Tangential Component
•
According to Ampere's circuital law,
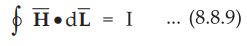
•
Consider a rectangular closed path abcda as shown in the Fig. 8.8.1. It is
traced in clockwise direction as a-b-c-d-a. This closed path is placed in a
plane normal to the boundary surface. Hence 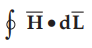 can be divided into 6
parts.
can be divided into 6
parts.
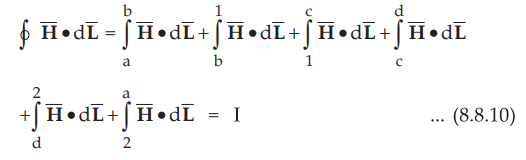
•
From the Fig. 8.8.1 it is clear that, the closed path is placed in such a way
that its two sides a-b and e-d are parallel to the tangential direction to the
surface while the other two sides are normal to the surface at the boundary.
This closed path is placed in such a way that half of its portion is in medium
1 and the remaining is in medium 2. The rectangular path is an elementary
rectangular path with elementary height Ah and elementary width Δw. Thus over
small width Δw, ![]() can be assume constant say Htan1 in medium
1 and Htan2 in medium 2. Similarly over a small height
can be assume constant say Htan1 in medium
1 and Htan2 in medium 2. Similarly over a small height 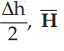 can
be assumed
can
be assumed
constant
say HN1 in medium 1 and HN2 in medium 2. Now assume that ![]() is the surface current normal to the path. Also from the Fig. 8.8.1 it
is clear that the normal and tangential components in medium 1 and medium 2 are
in opposite direction. Thus equation (8.8.10) can be written as,
is the surface current normal to the path. Also from the Fig. 8.8.1 it
is clear that the normal and tangential components in medium 1 and medium 2 are
in opposite direction. Thus equation (8.8.10) can be written as,
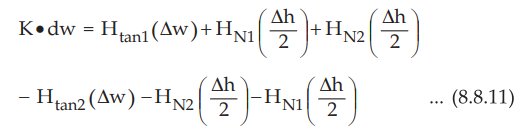
•
To get conditions at boundary, Δh → 0.
Thus,
K•
dw = Htan1 (Δw) - Htan2 (Δw)
Htan1
- Htan2
In
vector form, we can express above relation by a cross product as
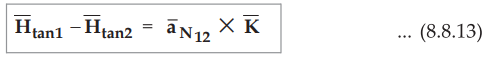
•
where 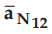 is the unit vector in the direction normal at the boundary
from medium 1 to medium 2.
is the unit vector in the direction normal at the boundary
from medium 1 to medium 2.
•
For ![]() , the tangential components can be related with permeabilities
of two media using equation (8.8.12),
, the tangential components can be related with permeabilities
of two media using equation (8.8.12),

•
Consider a special case that the boundary is free of current. In other words,
media are not conductors; so K = 0. Then equation (8.8.12) becomes
Htan1
- Htan2 = 0
Or
Htan1 - Htan2 ….. (8.8.15)
• For tangential components of ![]() we
can write,
we
can write,
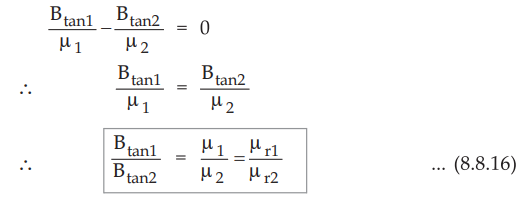
•
From equations (8.8.15) and (8.8.16) it is clear that tangential component of ![]() are continuous, while tangential component of
are continuous, while tangential component of ![]() are discontinuous at
the boundary, with the condition that the boundary is current free.
are discontinuous at
the boundary, with the condition that the boundary is current free.
•
Let the fields make angles a1 and a2 with the normal to
the interface as shown in the Fig. 8.8.2.
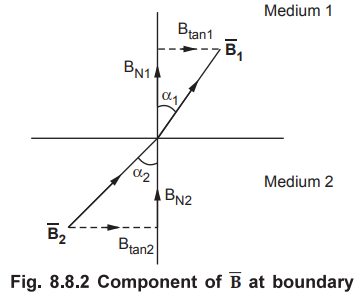
•
Interms of angle a1 and a2, we can write relationship
between normal components and tangential components of ![]() .
.
In
medium 1,
tan
ɑ1 = Btan1 / BN1 ….. (8.8.17)
•
Similarly in medium 2,
tan
ɑ2 = Btan2 / BN2 ….. (8.8.17)
As
we know, BN1 = BN2
•
Consider an interface between air (medium 1) and soft iron (medium 2). For air,
µr1 = 1. For soft iron, let µr2 = 7000. Then
Btan1
/ Btan2 = tan ɑ1 / tan ɑ2 = 1 / 7000
If
ɑ2 = 85°, then ɑ1 = 0.093° and Btan1 = 0.
•
Thus practically when fields cross a medium of high µr to low µr, then the
magnetic fields  are always perpendicular to the boundary.
are always perpendicular to the boundary.
Ex.
8.8.1 Given that 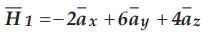 in region y - x - 2 ≤ 0 where µ1 = 5µ0, calculate
in region y - x - 2 ≤ 0 where µ1 = 5µ0, calculate  in the region y - x – 2 ≥ 0 where µ1 = 2µ0
in the region y - x – 2 ≥ 0 where µ1 = 2µ0
Sol.
:
As y – x – 2 ≤ 0 is a plane , the region 1 is given as y - x ≤ 2 , i.e. y ≤ x +
2

Let the surface be defined as,
f(x,y)
= y – x - 2
Then
the unit vector normal to the plane is given by,

Ex.
8.8.2 There exists a boundary between two magnetic material at z = 0, having
permittivities µ1 = 4 µ0 for region 1 where z > 0 and µ2 = 7 µ0 for region 2
where z < 0. For a field 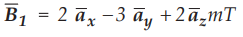 in region 1, find tangential component
of magnetic field intensity in region 2. Surface current density at boundary z
= 0 is 60
in region 1, find tangential component
of magnetic field intensity in region 2. Surface current density at boundary z
= 0 is 60 ![]() A/m.
A/m.
Sol.
:
From the given data, it is clear that z = 0 plane separates two magnetic
materials. That means z-axis is normal to the boundary. Then normal component
of ![]() is given by
is given by
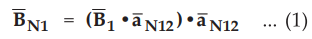
Now
above z = 0 there exists 1st magnetic material with µ1 = 4 µ0
while below z = 0, there exists
2nd magnetic material 1 to material 2.
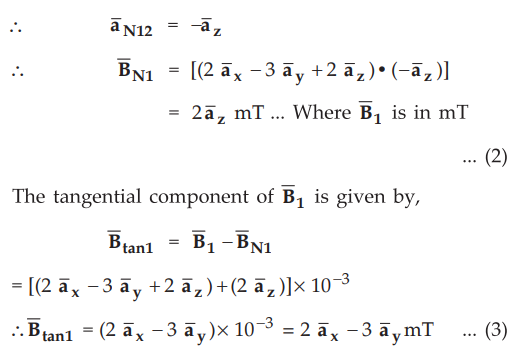
•
According to boundary condition, the normal component is continuous. Hence we
can write,
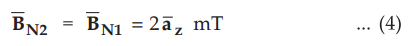
Now
according to boundary condition, for tangential component we can write,

Thus
from equations (4) and (8), the magnetic field in 2nd material is given by,

Ex.
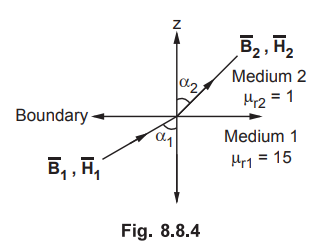
8.8.3 In region 1, as shown in the Fig. 8.8.4

Determine  in other medium and also calculate the angles made by the fields
with the normal.
in other medium and also calculate the angles made by the fields
with the normal.
Sol.
:
Assume that the boundary is current free.
In
medium 1,
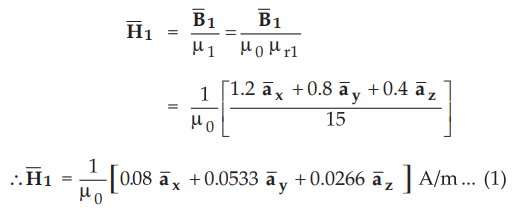
As
per the boundary shown in the Fig. 8.8.4, x and y are tangential, while z
component is normal. So according to the boundary conditions for current free
boundary, the tangential component for 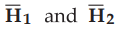 remain same. The normal
component can be calculated as
remain same. The normal
component can be calculated as

From
equation (1), the normal component i.e. component in z-direction is

Then
the magnetic flux density in medium 2 is given by
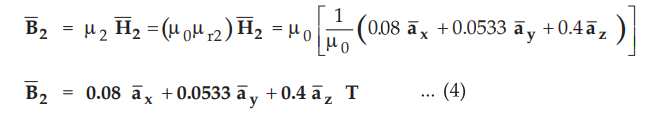
As
z-direction is perpendicular to boundary, in medium 1, we can write,
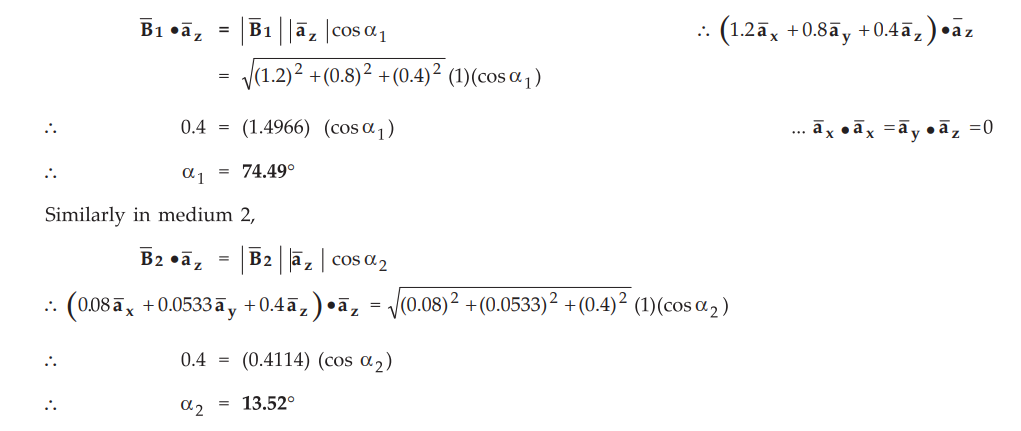
The
fields make angle 74.49° in medium 1 while 13.52° in medium 2.
Ex.
8.8.4 A current sheet  A/m is located at z = 0. The region 1 which is
at z < 0 has µr1 =4 and region 2 which is at z > 0 has µ r2
= 3. Given
A/m is located at z = 0. The region 1 which is
at z < 0 has µr1 =4 and region 2 which is at z > 0 has µ r2
= 3. Given 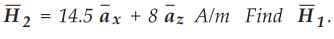
Sol.
: From
the given data, z-axis is normal to the boundary. The normal component of 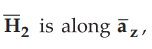 i.e. HN2 = 8 A/m. Similarly the tangential
component of
i.e. HN2 = 8 A/m. Similarly the tangential
component of 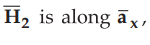 = 4.5 A/m.
= 4.5 A/m.
As
there is a current sheet at z = 0, tangential component of ![]() is not
continuous at the boundary. For the boundary containing current sheet we must
write,
is not
continuous at the boundary. For the boundary containing current sheet we must
write,
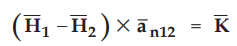
where  is unit vector normal to the boundary drawn from medium 1 to
medium 2. In this case
is unit vector normal to the boundary drawn from medium 1 to
medium 2. In this case
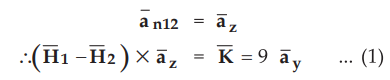
For
the boundary containing a current sheet, normal component of ![]() is
discontinuous. So we can write,
is
discontinuous. So we can write,

Examples
for Practice
Ex.
8.8.5 Let the permittivity be 5 uH/m in
region A where x < 0 and 20 uH/m in the region B where x > 0. If there is
surface current density

Ex.
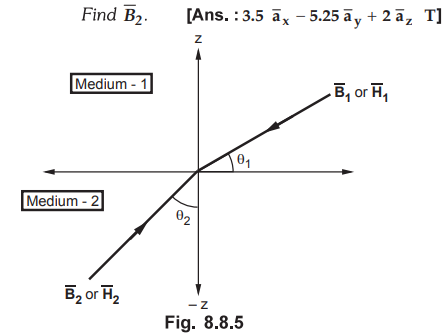
8.8.6 In the Fig. 8.8.5 shows 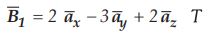 is incident on xy plane (z = 0). The medium 1 at z > 0 has µ1 =
4 µ0 z < 0 has µ2 = 7µ0
is incident on xy plane (z = 0). The medium 1 at z > 0 has µ1 =
4 µ0 z < 0 has µ2 = 7µ0
Ex.
8.8.7 Region 1 is the semi-infinite space in
which 2x-5y>0, while region 2 is defined by 2x -5y < 0. Let µr1=
3, µr2 = 4 and
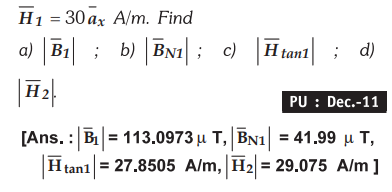
Ex.
8.8.8 Two regions are separated by a surface
3x - 2y + 5z = 0 . Region 1 has permeability µ1 = 2µ0 and
region 2 has µ2 = 5µ0. The point ϕ (2,2,2) lies in the
region 2 for a field
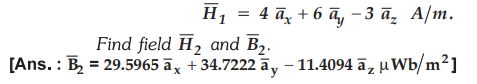
Review Questions
1. Write a short note on boundary conditions in magnetic field.
2. Derive the boundary conditions to explain the behaviour of
magnetic field at the interface of two magnetic media.
AU : Dec.-11, Marks 16; Dec.-14, 17, May-17, Marks 8
Electromagnetic Theory: Unit III: (b) Magnetic Forces, Magnetic Materials and Inductance : Tag: : with Example Solved Problems - Magnetic Boundary Conditions
Related Topics
Related Subjects
Electromagnetic Theory
EE3301 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
