Magnetic Circuits

Magnetic Circuits

AU : Dec.-02,10,11,13,17,18,19, May-11,13,14,19

 • The magnetic circuit can be defined as, the closed path traced by the magnetic lines of force i.e. flux. Such a magnetic circuit is associated with different magnetic quantities as m.m.f., flux reluctance, permeability etc.

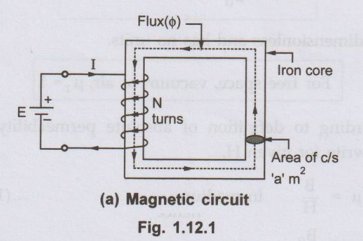
 • Consider simple magnetic circuit shown in the Fig. 1.12.1 (a). This circuit consists of an iron core with cross-sectional area of 'a' m2 with a mean length of 'l' m. (This is mean length of the magnetic path which flux is going to trace.) A coil of N turns is wound on one of the sides of the square core which is excited by a supply. This supply drives a current I through the coil. This current carrying coil produces the flux (0) which completes its path through the core as shown in the Fig. 1.12.1 (a) 

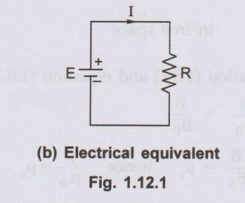
• This is analogous to simple electric circuit in which a supply i.e. e.m.f. of E volts drives a current I which completes its path through a closed conductor having resistance R. This analogous electrical circuit is shown in the Fig. 1.12.1 (b).

Let us derive relationship between m.m.f., flux and reluctance.

I = Current flowing through the coil,

N = Number of turns.

ϕ = Flux in webers,

B = Flux density in the core.

µ = Absolute permeability of the magnetic material

µ_r = Relative permeability of the magnetic material 

Magnetic field strength inside the solenoid is given by,

where NI = Magnetomotive force m.m.f. in AT

S = l/µ₀ µ_ra  = Reluctance offered by the magnetic path.

This expression of the flux is very much similar to expression for current in electric circuit.

I = e.m.f. /resistance

Key Point : So current is analogous to the flux, e.m.f. is analogous to the m.m.f. and resistance is analogous to the reluctance.

 

Ex. 1.12.1 A toroidal core made of mild steel has a mean diameter of 16 cm and a cross - sectional area of 3 cm2. Calculate a) the m.m.f to produce a flux of 4x10-4 Wb and b) the corresponding values of the reluctance of the core and the relative permeability. AU : Dec.-17, Marks 15

Sol. :

 

1. Series Magnetic Circuits

• In practice magnetic circuit may be composed of various materials of different permeabilities, of different lengths and of different cross-sectional areas. Such a circuit is called composite magnetic circuit. When such parts are connected one after the other the circuit is called series magnetic circuit.            

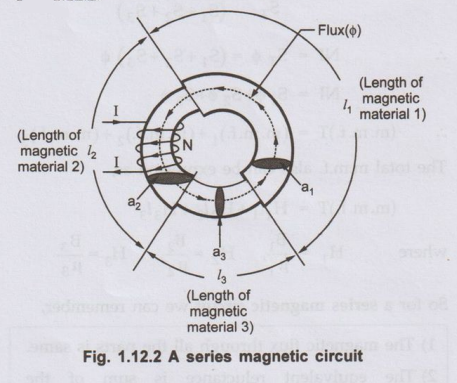
• Consider a circular ring made up of different materials of lengths l₁, l₂ and l₃ and with cross-sectional areas a₁, a2, and a₃ with absolute permeabilities µ₁, µ₂ and µ3 as shown in the Fig. 1.12.2

Let coil wound on ring has N turns carrying a current  of I amperes.

The total m.m.f. available is = NI AT

This will set the flux 'ϕ’ which is same through all the three elements of the circuit.

This is similar to three resistances connected in series in electrical circuit and connected to e.m.f. carrying same current 'T' through all of them.

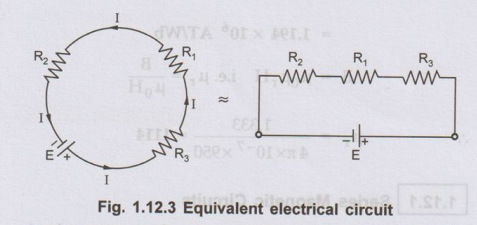
Its analogous electric circuit can be shown as in the Fig. 1.12.3.

The total resistance of the electric circuit is R₁ + R₂ + R₃. Similarly the total reluctance of the magnetic circuit is,

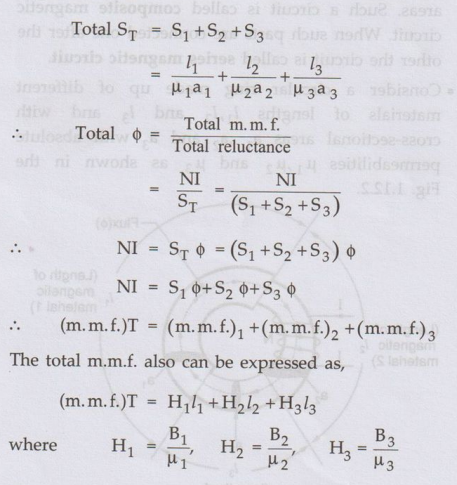
So for a series magnetic circuit we can remember,

1) The magnetic flux through all the parts is same.      

2) The equivalent reluctance is sum of the reluctance of different parts.

3) The resultant m.m.f. necessary is sum of the m.m.f.s in each individual part.

 

2. Series Circuit with Air Gap

• The series magnetic circuit can also have a short air gap.

Key Point : This is possible because we have seen earlier that flux can pass through air also.

Such air gap is not possible in case of electric circuit.

Consider a ring having mean length of iron part as ' li' as shown in the Fig. 1.12.4.

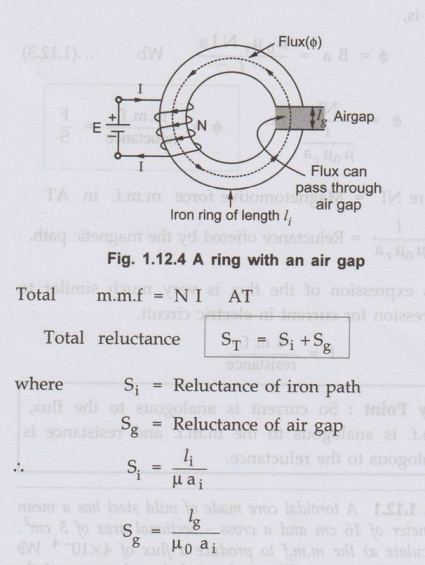
Key Point : The absolute permeability of airma µ = µ₀

The cross-sectional area of air gap is assumed to be equal to area of the iron ring.

 

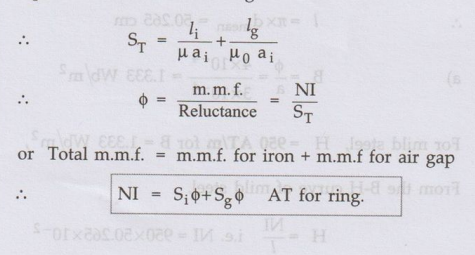
Ex 1.12.2 A ring has a diameter of 24 cm and a cross sectional area of 1000 mm . The ring is made up of semicircular sections of cast iron and cast steel with each joint having a reluctance equal to an air-gap of 0.2 mm. Find the ampere turns required to produce a flux of 8x 10^-4 Wb. The relative permeability of cast-steel and cast-iron are 900 and 170 respectively. Neglect fringing and leakage effects.

AU : Dec.-18, Marks 13

Sol. : The ring is shown in the Fig. 1.12.5.

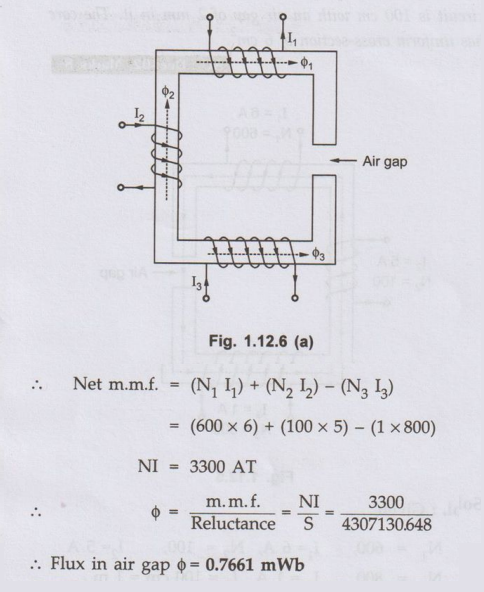
Ex. 1.12.3 A magnetic circuit is excited by three coils as shown in the Fig. 1.12.6. Calculate the flux produced in the air gap. The material used for core is iron having relative permeability of 800. The length of the magnetic circuit is 100 cm with an air gap of 2 mm in it. The core has uniform cross-section of 6 cm². AU : Dec.-02, Marks 8

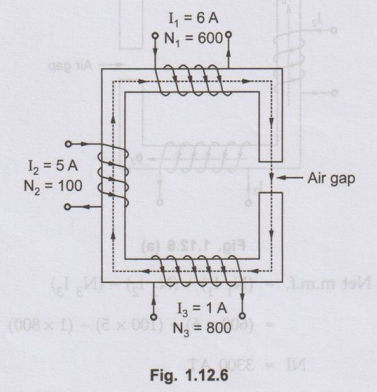
Sol. : Given,

  

Let us find the direction of flux due to various coils using right hand thumb rule.

As shown in the Fig. 1.12.6 (a) m.m.f. of coil (1) and (2) are in same direction while m.m.f. of coil (3) is in opposite direction.

 

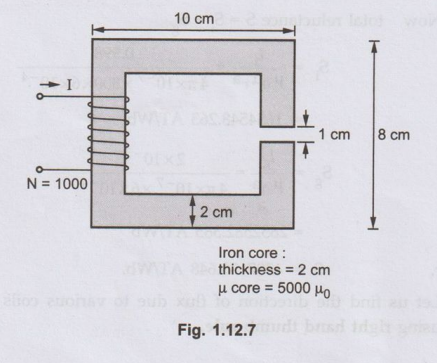
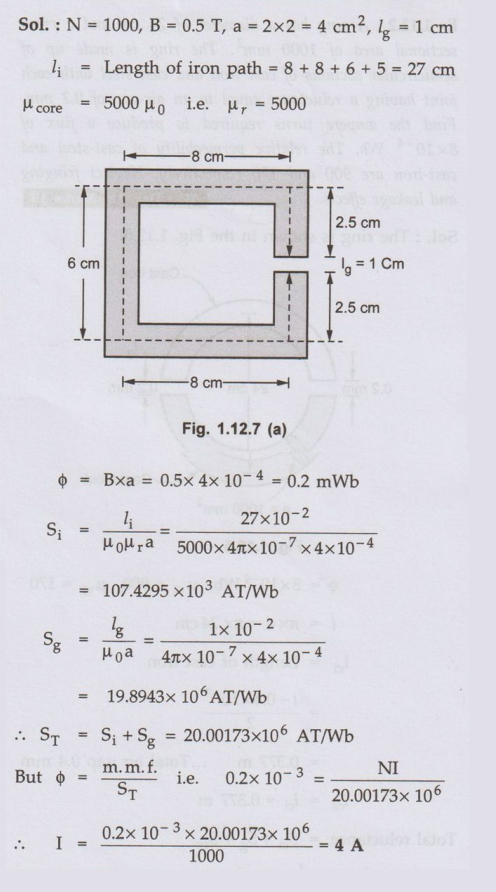
Ex. 1.12.4 For the magnetic circuit shown in Fig. 1.12.7 determine the current required to establish a flux density of 0.5 T in the air gap. AU : Dec.-10, Marks 12

Sol. :

 

Ex. 1.12.5 A ring composed of three sections. The cross section area is 0.001 m² for each section. The mean arc length are l_a = 0.3 m, l_b = 0.2 m, l_c = 0.1 m, an air gap length of 0.1 mm is cut in the ring, µ_r for sections a, b and c are 5000, 1000 and 10000 respectively. Flux in the air gap is 7.5x10^-4 Wb. Find i) m.m.f. ii) Exciting current if the coil has 100 turns iii) Reluctance of the sections. AU : Dec.-11, Marks 16

Sol. :

 

Ex. 1.12.6 A flux density of 1.2 Wb/m2 is required in 1 mm air gap of an electromagnet having an iron path of 1.5 m long. Calculate the mmf required. Given the relative permeability of iron = 1600. AU : Dec.-19, May-13, Marks 8

Sol. :

 

Ex 1.12.7 A steel ring has a mean diameter of 20 cm, a cross section of 25 cm² and a radial air-gap of 0.8 mm cut across it. When excited by a current of 1 A through a coil of turns 1000 wound on the ring core, it produces an air-gap flux of 1 mWb. Neglecting leakage and fringing. Calculate i) Relative permeability of steel and ii) Total reluctance of the magnetic circuit AU : Dec.-13, Marks 16

Sol. :

 

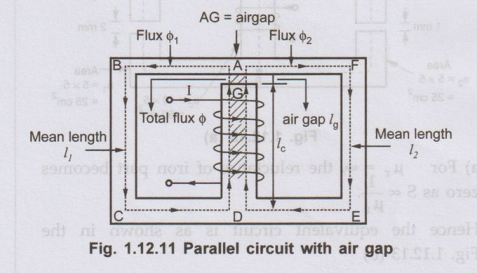
3. Parallel Magnetic Circuit

• In case of electric circuits, resistances can be connected in parallel. Current through each of such resistances is different while voltage across all of them is same. Similarly different reluctances may be in parallel in case of magnetic circuits. A magnetic circuit which has more than one path for the flux is known as a parallel magnetic circuit.

Consider a magnetic circuit shown in the Fig. 1.12.10 (a).     

At point A the total flux ϕ divides into two parts ϕ₁ and ϕ₂

ϕ = ϕ₁ +  ϕ₂

The fluxes ϕ₁ and ϕ₂ have their paths completed through ABCD and AFED respectively.

This is similar to division of current in case of parallel connection of two resistances in an electric circuit. The analogous electric circuit is shown in the Fig. 1.12.9 (b).

The mean length of path ABCD = l₁ m

The mean length of path AFED = l₂ m

The mean length of path AD = l_c m

The reluctance of path ABCD = S₁

The reluctance of path AFED = S₂

The reluctance of path AD = S_C

The total m.m.f. produced = N I AT

flux = m.m.f. / Reluctance

m.m.f. = ϕ × S

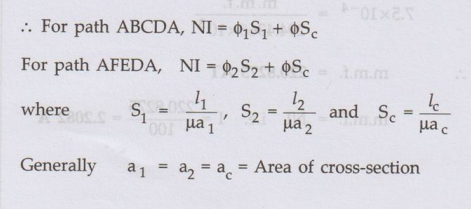
For parallel circuit,

Total m.m.f. required by central limb + m.m.f. required by any one outer limbs

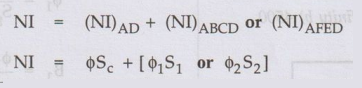
As in the electric circuit e.m.f. across parallel branches is same, in the magnectic circuit the m.m.f. across parallel branches is same.

Thus same m.m.f. produces different fluxes in the two parallel brancges. For such parallel branches,

ϕ₁ S₁ = ϕ₂ S₂

Hence while calculating total m.m.f., the m.m.f. of only one of the two parallel branches must be considered

 

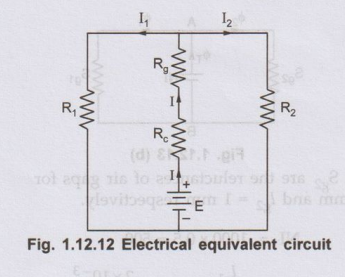
4. Parallel Magnetic Circuit with Air Gap

Consider a parallel magnetic circuit with air gap in the central limb as shown in the Fig. 1.12.11. 

The analysis of this circuit is exactly similar to the parallel circuit discussed above. The only change is the analysis of central limb. The central limb is series combination of iron path and air gap. The central limb is made up of,

Thus the electrical equivalent circuit for such case becomes as shown in the Fig. 1.12.12.

Similarly there may be air gaps in the side limbs but the method of analysis remains the same.

 

Ex. 1.12.8 For the magnetic circuit shown in Fig. 1.12.13, with a core thickness 5 cm, exciting current of 0.5 A with 1000 turns coil, find the flux density and flux in each of the outer limbs and the central limbs. Assume relative permeability for iron of the core to be a) infinity b) 4500.

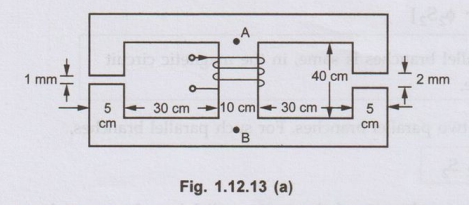
 Sol. : The fluxes are shown in the Fig. 1.12.13 (a)                                             

Key Point : The m.m.f. (NI) remains same for the parallel paths.

b) For µ_r = 4500, the equivalent circuit is as shown in the Fig. 1.12.13 (c)

Ex. 1.12.9 In the magnetic circuit detailed in Fig. 1.12.14 (a) with all dimensions in mm, calculate the required current to be passed in the coil having 200 turns in order to establish a flux of 1.28 mWb in the air gap. Neglect fringing effect and leakage flux. The B-H curve of the material is given in Fig. 1.12.14 (b). Permeability of air may be taken as µ₀ = 41x10^-2 H/m. AU : May-19, Marks 15

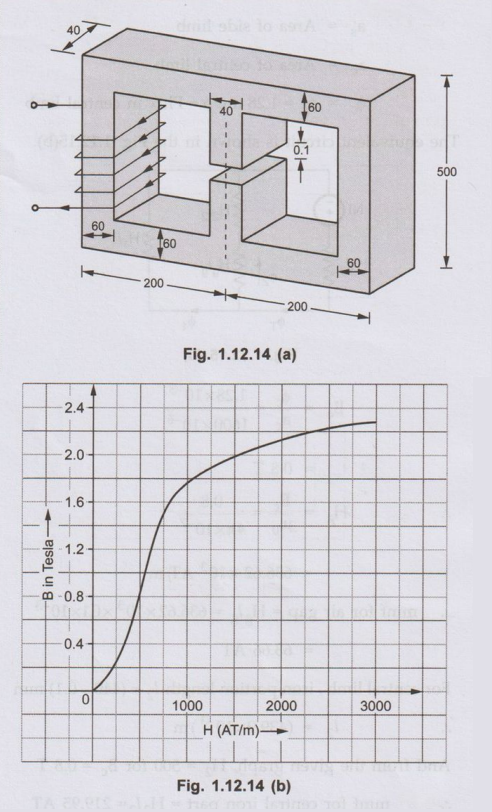
Sol. :

The simplified diagram is shown in the Fig.1.12.15 (a).

Review Questions

1. Discuss in detail about magnetic circuits. AU : May-11, Marks 5

2. Draw and explain the typical magnetic circuit with air-gap and its equivalent electric circuit. Hence derive the expression for air-gap flux. AU : Dec.-17, May-13, 14, Marks 16

3. A steel ring of 180 cm mean diameter has a cross sectional area of 250 mm2. Flux developed in the ring is 500 u Wb when a 4000 turns coil carries certain current. Find   i) m.m.f. required ii) reluctance iii) current in the coil. Given that the relative permeability of the steel is 1100. 

(Ans. : 8181.72 AT, 1.6363 x 107, 2.045 A)       

4. A coil is wound uniformly with 300 turns over a steel ring of relative permeability 900, having mean circumference of 40 mm and cross-sectional area of 50 mm². If a current of 25 A is passed through the coil, determine     

i) m.m.f. ii) reluctance of ring and iii) flux.

(Ans. : 7500 AT, 707355.3 AT/Wb, 0.0106 Wb)

5. Find the number of ampere turns required to produce a flux of 0.44 milli-weber in an iron ring of 100 cm mean circumference and 4 cm² in cross-section. B Vs ur test for the iron gives the following result :

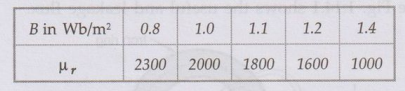
If a saw cut of 2 mm wide is made in the above ring, how many extra ampere turns are required to maintain same flux ? 

(Ans. : 486.307 AT, 1744 AT)                            

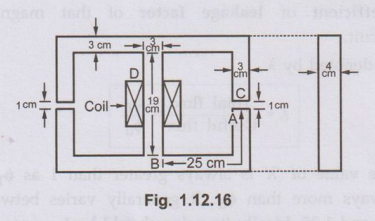
6. The Fig. 1.12.16 shows a magnetic circuit with two similar branches and an exciting coil of 1500 turns on central limb. The flux density in the air gap is 1 Wb/m² and leakage coefficient 1.2. Determine exciting current through the coil. Assume relative permeability of the iron constant equal to 600.

(Ans. : I = 6.2388 A)

7. A magnetic circuit has the mean length of flux path f 20 cm, and cross sectional area of 1 cm². Relative permeability of its material is 2400. Find the m.m.f. required to produce a flux density of 2 tesla in it. If an airgap of 1 mm is introduced in it, find the m.m.f. required for the air gap as a fraction of the total m.m.f. to maintain the same flux density.

(Ans. : 0.9234 times total m.m.f)