Magnetic circuits

Magnetic circuits

AU : May-04, 10, 13, 16, 18, Dec.-14

• In general, in magnetic circuits, we determine the magnetic fluxes and magnetic field intensities in various parts of the circuits. The magnetic circuits are analogous to the electric circuits. If we study this analogy between the electric and magnetic circuits, we can achieve simple techniques for analysis of the magnetic circuits. Also we can directly use the concepts of the electric circuits in solving the magnetic circuit problems.

• The common examples of the magnetic circuits are transformers, toroids motors, generators, relays and magnetic recording devices.

• Let us study analogy between the electric and magnetic circuits. An electric circuit forms a circuit (i.e. closed path) through which current can flow. Similar to this magnetic lines of flux are continuous and can form closed paths. So a single magnetic line  of flux or all parallel magnetic lines of flux may be considered as magnetic circuit.

• Similar to electromotive force (e.m.f.) in an electric circuit, we can define a new quantity in case of a magnetic circuit called magnetomotive force (m.m.f.). The magnetomotive force (m.m.f.) is defined as,

• The SI unit of m.m.f. is ampere (A). But generally, in magnetic circuits, the source of m.m.f. is a coil carrying conductors with N number of turns as shown in the Fig. 8.9.1 (c). Thus m.m.f. is measured in ampere-turn (A-t) very often. Note that m.m.f. is not a force measured in newton.

• In an electric circuit, resistance is defined as the ratio of voltage to current given by

R = V / I

• In case of analogous magnetic circuits, we define a new quantity reluctance (R) as the ratio of the magnetomotive force to the total flux.

Ɽ = em / ϕ ….. (8.9.2)

The reluctance is measured in Ampere . turn / Weber

• The resistance in electric circuit can be expressed interms of conductivity σ as

R =  l / σS

 

where

l = Length in m

S = Cross-sectional area in m2

σ = Conductivity of the linear isotropic homogeneous material.

• In case of magnetic circuits, we can define reluctance in very much similar way as,

R  = l / µS  ... (8.9.3)

where          µ = Permeability of the isotropic, linear homogeneous material

• For electric circuit, Ohm's law can be expressed in point from as,

• Now consider magnetic circuit. The magnetic flux density is analogous to the current density, thus we can write,

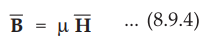
• The basic equations derived in magnetostatics are very much helpful in the analysis of the magnetic circuits. These basic equations are

• In other form, the two equations can be expressed in terms of the total current flowing in the magnetic circuit and the total magnetic flux density through cross-section of the magnetic circuit.

• The total current in the magnetic circuit is given by,

• The total magnetic flux density flowing through the cross-section of the magnetic circuit is given by

• In electric circuit, The reciprocal of the resistance is called conductance. In magnetic circuits, the reciprocal of the reluctance is called permeance denoted by p The permeance is measured in henries (H).

P = µS / l ... (8.9.9)

• The analogous electric and magnetic circuits can be represented in simple way as shown in the Fig. 8.9.1.

• In electric circuits we can apply basic Kirchhoff s laws; such as Kirchhoff's Current Law (KCL) at the node and Kirchhoff's Voltage Law (KVL). We can apply the same laws to the magnetic circuits. There are two laws namely Kirchhoff's flux law and Kirchhoff’s m.m.f. law.

• Kirchhoff's flux law states that the total magnetic flux arriving at any junction in a magnetic circuit is equal to the total magnetic flux leaving that junction. Using this law, parallel magnetic circuits can be easily analyzed. Mathematically, Kirchhoff's flux law at a junction can be expressed as,

∑ ϕ  = 0  ... (8.9.10)

• Kirchhoff's m.m.f. law states that the resultant m.m.f. around a closed magnetic circuit is equal to the algebraic sum of products of flux and reluctance of each part of the closed circuit. For closed magnetic circuit,

∑ M. M. F = ∑ ϕ R ... (8.9.11)

• Kirchhoff's m.m.f. law can be alternatively stated as resultant m.m.f. around any closed loop of a magnetic circuit is equal to the algebraic sum of the products of the magnetic field strength and the length of each part of the circuit. Hence we can write,

∑ M. M. F = ∑ H . l ... (8.9.12)

• Inspite of having analogous behaviour of the magnetic circuits with the electric circuits, it is very difficult to carryout exact analysis of the magnetic circuits. The difficulties in the analysis are due to the following points.

• In general, the magnetic circuits are made up of ferromagnetic material. The permeability of ferromagnetic materials depends on the magnentic field intensity  .

• Secondly, it is difficult to control and calculate the leakage flux which strays or leaks from the main path of the flux in the magnetic circuit.

• Lastly if there is an air gap in between the path of the magnetic flux, it spreads and bulges out. This effect is called fringing effect.

The analogy between the electric circuit and magnectic circuit is summarized in Table 8.9.1.

• The dissimilarities between the electric and Magnetic circuit are given in Table 8.9.2.

 

Ex. 8.9.1 An iron ring with a cross-sectional area of 3 cm2 and a mean circumference of 15 cm is wound with 250 turns wire carrying a current of 0.3 A. The relative permeability of the ring is 1500. Calculate the flux established in the ring.

AU: Dec.-14, Marks 8, May-18, Marks 13

Sol. : The magnetic field intensity is given by,

H = I / 2лг = I/C = 0.3 / 15 × 10^-2 = 2 A/m

where   C = Circumference

But B = µH = µ₀ µ_r H

= 4 × π × 10^-7 × 1500 × 2 = 3.7699 × 10^-3 T

The flux induced in one turn of a iron ring is given by,

ϕ = B.S where

S = Area of cross-section of iron ring

= (3.7699 × 10^-3) (3 × 10^-4)

= 1.13097 × 10^-6 Wb

Hence the total flux established in the ring for N number of turns is given by,

ϕ_Total = N. ϕ = 250. (1.13097 × 10^-6)

= 0.2827 mWb

Ex. 8.9.2 An iron ring with a cross-sectional area of 3 cm2 and a mean circumference of 15 cm is wound with 250 turns of wire carrying a current of 0.3 A. The relative permeability of the ring is 1500.

i) Calculate the flux established in the ring.

ii) If a saw cut of width 2 mm is made in the above ring, find the new value of the flux in the circuit.

Sol. : For solution of  i), refer example 8.9.1.

ii) With saw cut air gap in a iron ring, total reluctance is given by,

R_T = Reluctance of iron ring + Reluctance of air gap

 

Ex. 8.9.3 An iron ring with a cross sectional area of 8 cm and a mean circumference of 120 cm is wound with 480 turns of wire carrying a current of 2 A. The relative permeability of the ring is 1250. Calculate the flux established in the ring. 

The magnetic field intensity is given by,

The flux induced in one turn of an ion ring is given by,

Hence the total flux induced in the iron ring of 480 turns is given by,

 

Ex. 8.9.4 A coil has 1000 turns and carries a magnetic flux of 10 mWb. The resistance of the coil is 4 Q. If it is connected to a 40 V d.c. supply, estimate the energy stored in the magnetic field when the current attains its final steady state value.

Sol. : Given : N = 1000, ϕ = 10 mWb = 10 × 10^-3 Wb,

R = 4 Ω, V = 40 V

The current in the coil at steady state is given by,

I = V / R = 40 / 4 = 10 A

Hence the self inductance of a coil is given by,

L = N ϕ / I = 1000 × 10 × 10^-3 / 10 = 1 H

Thus the energy stored in a magnetic field is given by,

W_m = 1/2 LI² = 1/2 (1) (10)² = 50 W

 

Examples for Practice

Ex. 8.9.5 A cast iron C core has a mean length of 0.44 m with square cross-section 0.02 × 0.02 m. The air gap length is 2 mm and the coil has 400 turns. Find the current required to establish an air gap of 0.141 mWb, µr = 328.

[Ans. : 2.0932 A]

Ex. 8.9.6 A magnetic circuit employes an air core toroid with 500 turns, cross sectional area 6 cm², mean radius 15 cm and 4 A coil current. Determine reluctance of the circuit, flux density and magnetic field intensity.

[Ans. : 1.25 × 10⁹ A. t / Wb, 1.6 × 10^-6 Wb 2.667 × 10^-3 T, 2122.1 A.t/m]

Review Questions

1. Explain the relation between field theory and circuit theory.

2. Tabulate the similarities and dissimilarities of the electric and magnetic circuits.

3. Define a magnetic circuit with a sketch and hence obtain the expression for its reluctance.