Magnetic Field in Rotating Machines (Rotating Magnetic Field)

Magnetic Field in Rotating Machines (Rotating Magnetic Field)

AU: April-03, Dec.-03,06,07,08,09,10,12,16, May-03, 05, 07,11,14

• It is seen that the m.m.f. wave produced by the single phase a.c. winding is pulsating, whose amplitude varies sinusoidally with time. This is because the current flowing in single phase a.c. winding is alternating in nature.

• Now consider a magnetic field produced due to physical rotation of a permanent magnet in a space with a certain speed. It produces a magnetic field whose magnitude is constant but axis rotates in space with certain speed.

Key Point: Thus a magnetic field having constant amplitude but whose axis continuously rotates in a plane with a certain speed is called rotating magnetic field.

• In a pulsating m.m.f. wave, the axis is fixed while amplitude varies sinusoidally while in rotating magnetic field amplitude is constant but axis rotates with a certain speed.

• Consider a three phase a.c. winding, either star or delta connected supplied from a three phase a.c. supply. This is shown in the Fig. 2.12.1.

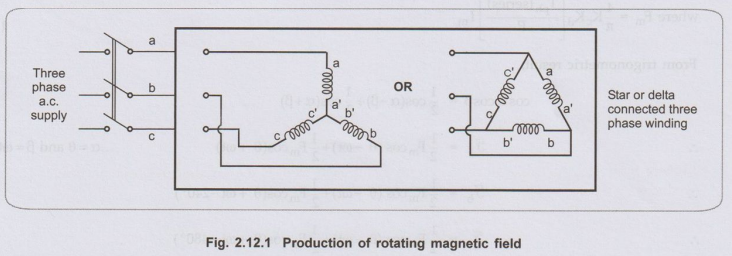
• The three sinusoidal phase currents simultaneously through the windings. These currents are displaced from each other by 120° electrical. These currents can be mathematically expressed as,

i_a   = I_m cos ωt ...(2.12.1a

i_b  = I_m cos (ωt-120°) ...(2.12.1b)

i_c   = I_m cos (ωt-240°) ...(2.12.1c)

The phase sequence is assumed to be a-b-c.

As the supply is balanced and windings are identical, the maximum value Im of each phase current is equal. These currents are shown in the Fig. 2.12.2. .

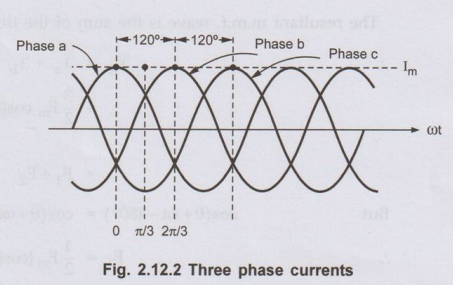
•  The instant is considered when phase a current has attained its maximum value. Such three currents produce three individual m.m.f. waves as discussed in the last section. These m.m.f. waves also displaced by 120° electrical from each other in space and their magnetic axes are coinciding with the axes of the respective phases as shown in the Fig. 2.12.3.

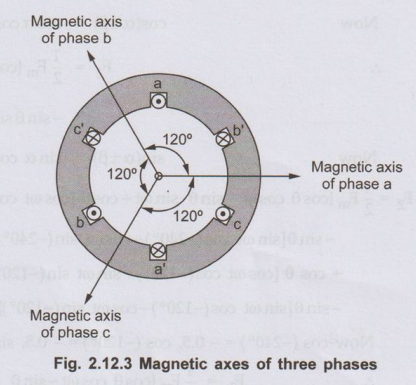
• As the three individual m.m.f waves are separated by 120^o electrical from each other in space, their mathematical representation can be obtained as,

• This equation shows that the resultant m.m.f. wave is a travelling wave. Its magnitude is constant equal to 3/ 2 F_m while its phase angle changes linearily with time as ωt. So its axis rotates in the air gap at a constant speed of ω rad(elect)/sec.

Key Point: This shows that when a three phase stationary windings are excited by balanced three phase a.c. supply then the resulting field produced is rotating magnetic field. Though nothing is physically rotating, the field produced is rotating in space having constant amplitude.

Thus at t₁ =0, F_R=3/2 F_m cosθ when phase a is at its maximum. Thus axis of resultant m.m.f coincides with the axis of the phase a.

At t₂ = 2π/3, F_R=3/2F_m cos( θ-2π/3 )and phase b is at its maximum. Thus axis of resultant m.m.f. coincides with the axis of phase b.

At t₃ = 4π/3 the axis of resultant m.m.f. coincides with the axis of phase c and so on.

Key Point: So if phase sequence is a-b-c, the rotating magnetic field rotates in the direction of phase sequence.

1. Speed of Rotating Magnetic Field

It is known that its speed is ω rad(elect)/sec. The mechanical angular velocity ωm is related to electrical ω as,

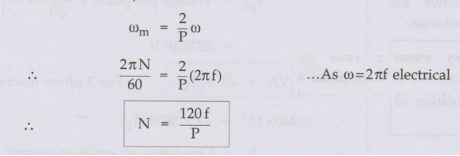
• This is the speed of the rotating magnetic field. This is called synchronous speed and denoted as Ns.

Key Point: Thus rotating magnetic field rotates with synchronous speed N_s.

2. Direction Rotating Magnetic Field

• The direction of the R.M.F. is always from the axis of the leading phase of the three phase winding towards the lagging phase of the winding. In a phase sequence of R-Y-B, phase R leads Y by 120° and Y leads B by 120°. So R.M.F. rotates from axis of R to axis of Y and then to axis of B and so on. So its 084 direction is clockwise as shown in the Fig. 2.12.4 (a). This direction can be reversed by interchanging any two terminals of the three phase windings while connecting to the three phase supply. The terminals Y and B are shown interchanged in the Fig. 2.12.4 (b). In such case the direction of R.M.F. will be anticlockwise.

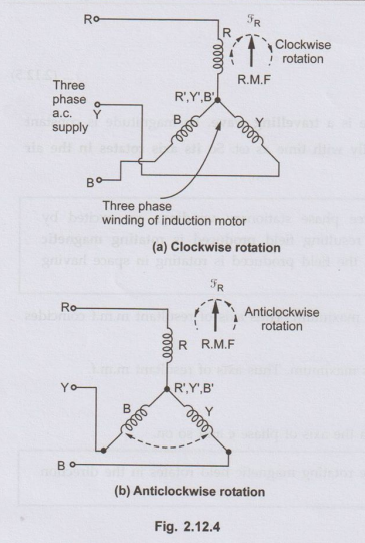
• As Y and of windings are connected to B and Y from winding point of view the phase sequence becomes R-B-Y. Thus R.M.F. axis follows the direction from R to B to Y which is anticlockwise.

Key Point : Thus by interchanging any two terminals of three phase winding while connecting it to three phase a.c. supply, direction of rotation of R.M.F. gets reversed.

3. Peak Value of Rotating Magnetic Field

• The resultant m.m.f. wave due to three phase a.c. winding is.

Where I_m = Maximum value of the phase current

Key Point: The rotating magnetic field is also called rotating m.m.f. wave in three phase a.c. machines.

• Neglecting reluctance of iron path, the resultant m.m.f. produces sinusoidal rotating flux density (B) wave in air gap whose peak value is given by,

B_peak = 3µ₀F_m / 2g

Where g =  Length of the air gap

Ex. 2.12.1 A 3-phase, 440 kVA, 50 Hz, star connected synchronous generator running at 400 r.p.m. is designed to develop 3600 between terminals. The armature consists of 180 slots, each slot having one coil side with eight conductors. Determine the peak value of the fundamental mmf in AT/pole when the machine is delivering full load current. AU: April-03, Marks 10

Sol.

Ex. 2.12.2 A 3 phase, 40 kW, 4 pole, 50 Hz induction motor has a winding (a.c.) designed for delta connection. The winding has 24 conductors per slot arranged in 60 slots. The r.m.s. value of the line current is 40 A. Find the fundamental of the m.m.f. wave of phase-A when the current is passing through its maximum value. What is the speed and peak value of the resultant m.m.f./pole?

AU: Dec.-07, 09, May-11, Marks 8

Sol.

Review Questions

1. Explain with the help of neat diagram about the nature of the rotating magnetic field produced when a three phase supply is connected across a three phase winding. AU: May-03, 05, 07, Dec.-03, 06, 08, 10, Marks 8

2. Explain the concept of rotating magnetic field. AU: Dec.-12, Marks 16

3. Prove that the resultant m.m.f. wave of three phase a.c.winding is rotating in space with speed ω but its magnitude is constant.

4. Explain briefly the production of rotating magnetic field. What are the speed and direction of rotation of the field? Is the speed uniform?