Magnetic field intensity (H) due to Straight Conductor of Finite Length

 due to Straight Conductor of Finite Length

• Consider a conductor of finite length placed along z axis, as shown in the Fig. 7.5.1.

• It carries a direct current I. The perpendicular distance of point P from z axis is r as shown in the Fig. 7.5.1. The conductor is placed such that its one end is at z = z₁ while other at z = z₂.

• Consider a differential element  along z axis, at a distance z from origin.

• The unit vector in the direction joining differential element to point P is  and can be expressed as shown in the Fig. 7.5.2.

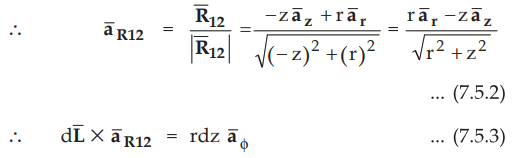
• This is same as obtained in the earlier section for infinitely long conductor.

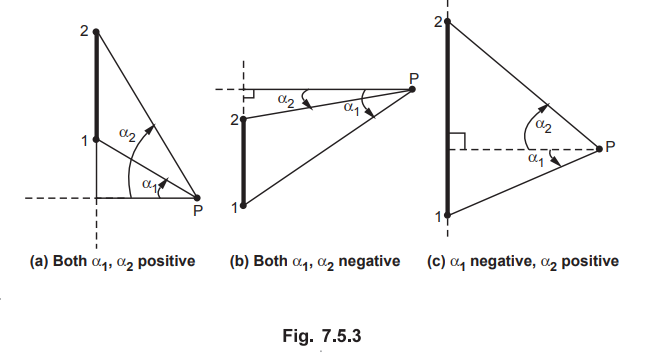
1. Sign Convention for a₁ and a₂

• If both the ends of conductor are above point P, then ɑ₁ and ɑ₂ are positive. If both the ends of conductor are below point P, then both ɑ₁ and ɑ₂ are negative. While if one end of the conductor is above P and other below then ɑ₁ is negative and ɑ₂ positive. This is shown in the Fig. 7.5.3.

• The result given by equation (7.5.8) can be used directly to obtain caused by current filaments which are arranged as the sequence of straight lines.

• Very important note : While using this result, if segment carrying current I is not along z axis then the direction of  can not be  It depends on in which plane segment carrying current is placed. The magnitude of  but direction

is always normal to the plane containing the source and to be decided by right handed screw rule.

Ex. 7.5.1 Find the magnetic field intensity at (1.5, 2, 3) due to a conductor carrying current of 24 A along z-axis extending from z = 0 to z = 6.

Sol. : The conductor is shown in the Fig. 7.5.4 (a).

Ex. 7.5.2 A conductor in the form of regular polygon of 'n' sides inscribed in a circle of radius R. Show that the expression for magnetic flux density is

at the centre, where I is the current. Show also when ’n’ is indefinitely increased then the expression reduces to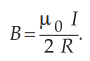 

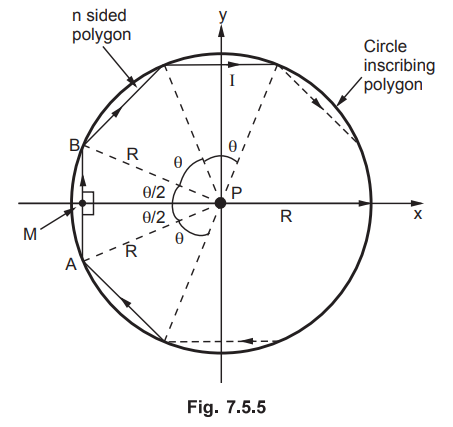
Sol. : Consider a polygon of n sides inscribed in a circle of radius R, as shown in the Fig. 7.5.5. It carries a current I.

Let the polygon is placed in the xy plane. Consider the side AB of polygon. The angle subtended by each side at the centre is say θ. The PM is perpendicular to AB. Thus ∠ BPM = ∠ AMP = θ / 2

Now as the sides are n, the angle θ can be written as,

Examples for Practice

Ex. 7.5.3 Find the magnetic flux density at the centre P of a square of sides equal to 5 m and carrying 10 amperes of current.

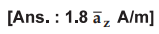
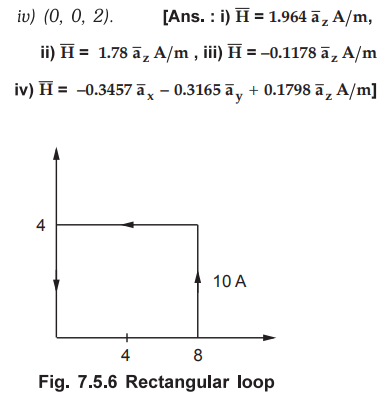
Ex. 7.5.4 A rectangular loop carrying 10 A current is placed on z = 0 plane as shown in Fig. 7.5.6. Evaluate  at :

i) (2, 2, 0) ii) (4, 2, 0) iii) (4, 8, 0) iv) (0, 0, 2).

Ex. 7.5.5 A circuit carrying a direct current of 5 A form a regular hexagon inscribed in a circle of radius 1 m. Calculate the magnetic flux density at the centre of the current hexagon. Assume the medium to be freespace.

[Ans.: B = 3.4641 µWb/m²]

Review Question

1. Find the expression for magnetic field intensity at a point in x-y plane, due to a finite length current element carrying current 1 lying along z-axis.

AU : May-17, Marks 8