Electromagnetic Theory: Unit III: (a) Magnetostatics
Magnetic field intensity (H) on the Axis of a Circular Loop
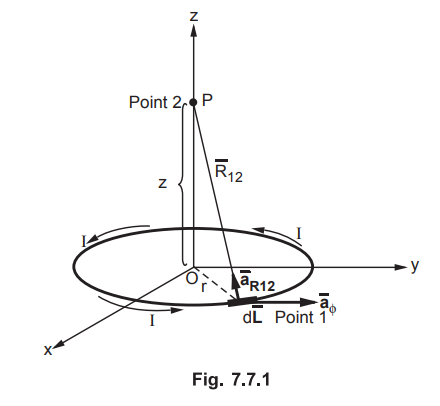
• Consider a circular loop carrying a direct current I, placed in xy plane, with z axis as its axis as shown in the Fig. 7.7.1.
![]() on the Axis of a Circular Loop
on the Axis of a Circular Loop
AU
: Dec.-02, 03, 08, 09, 10, 17, May-06, 09, 16, 18
•
Consider a circular loop carrying a direct current I, placed in xy plane, with
z axis as its axis as shown in the Fig. 7.7.1. The magnetic field intensity ![]() at point P is to be obtained. The point P is at a distance z from
the plane of the circular loop, along it's axis.
at point P is to be obtained. The point P is at a distance z from
the plane of the circular loop, along it's axis.
•
The radius of the circular loop is r. Consider the differential length ![]() of the circular loop as shown in the Fig. 7.7.1.
of the circular loop as shown in the Fig. 7.7.1.
•
In the cylindrical co-ordinate system,
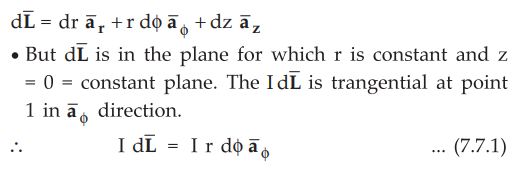
•
The unit vector 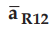 is in the direction along the line joining
differential current element to the point P.
is in the direction along the line joining
differential current element to the point P.
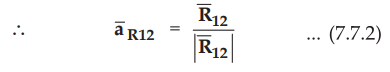
From
the Fig. 7.7.2, it can be observed that,
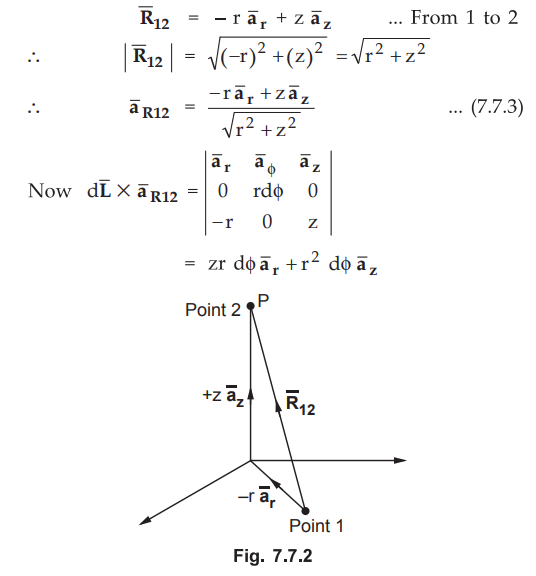
•
Note that while calculating cross product |R12| is neglected for
convenience, which must be considered in further calculations.
•
According to Biot-Savart law, the differential field strength ![]() at
point P is given by,
at
point P is given by,
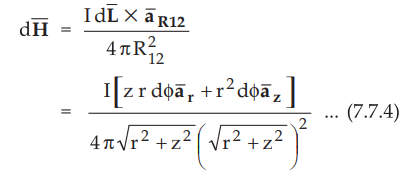
•
Note that |![]() | which was neglected while obtaining the cross
product is now considered in
| which was neglected while obtaining the cross
product is now considered in ![]() .
.
•
The total ![]() is to be obtained by integrating
is to be obtained by integrating ![]() over the
circular loop i.e. for ϕ = 0 to 2 π .
over the
circular loop i.e. for ϕ = 0 to 2 π .
Note
:
It can be observed that though ![]() consists of two components
consists of two components 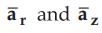 ,
due to radial symmetry all
,
due to radial symmetry all ![]() components are going to cancel each
other. So
components are going to cancel each
other. So ![]() exists only along the axis in
exists only along the axis in ![]() direction.
direction.
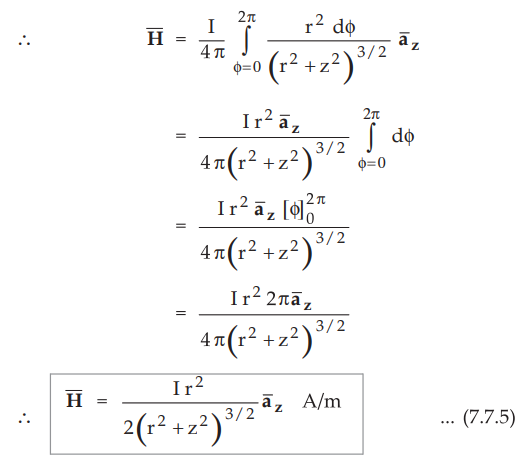
where r = Radius of the circular loop
z
= Distance of point P along the axis
Note
:
If point P is shifted at the centre of the circular loop i.e. z = 0, we get the
result obtained in earlier section.
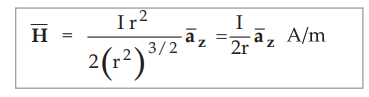
where ![]() is the unit vector normal to xy plane in which the circular loop
is lying.
is the unit vector normal to xy plane in which the circular loop
is lying.
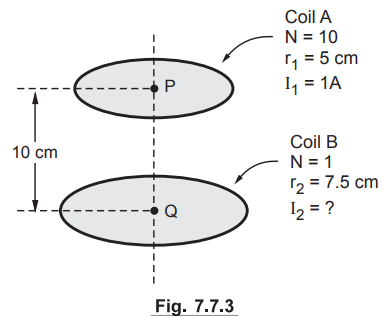
Ex. 7.7.1 Two narrow circular coils A and B have common axis and are placed 10 cm apart. The coil A has 10 turns of radius 5 cm with a current of 1 A passing through it. The coil B has a single turn of radius 7.5 cm. If the magnetic field at the centre of coil A is to be zero, what current should be passed through coil B.
Sol.
: The ![]() at the centre of the circular coil with N turns is given by,
at the centre of the circular coil with N turns is given by,
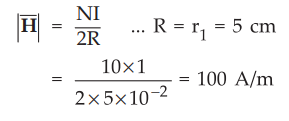
The ![]() at the centre of coil A i.e. point P due to coil
at the centre of coil A i.e. point P due to coil
B
is,
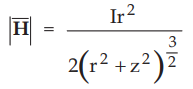
Where
r = r2 = 7.5 cm, I = I2
and
z = Distance between point P and coil = 10 cm
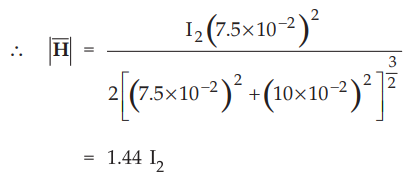
The
total ![]() at P = 100 + 1.44 I2 which must be zero,
at P = 100 + 1.44 I2 which must be zero,
I2
= -100 / 1.44 = - 69.44 A
The
negative sign indicates direction of I2, is opposite to that of I1.
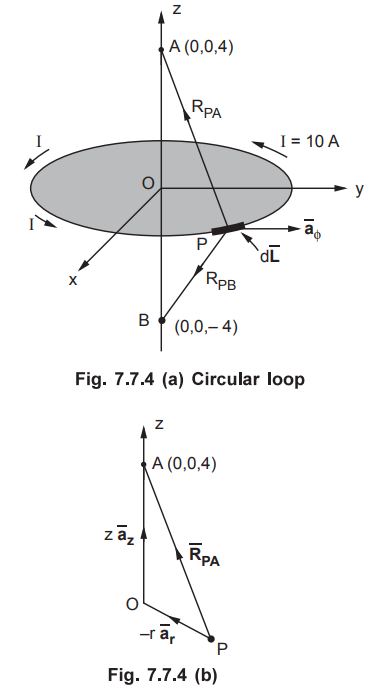
Ex.
7.7.2 A circular loop located on x2
+ y2 = 9, z = 0 carries a direct current of 10 A along ![]() Determine
Determine ![]() at (0,0,4) and (0,0,- 4).
at (0,0,4) and (0,0,- 4).
AU: Dec.-09, Marks 16
Sol.
: The
loop in x-y plane is shown in the Fig. 7.7.4 (a)
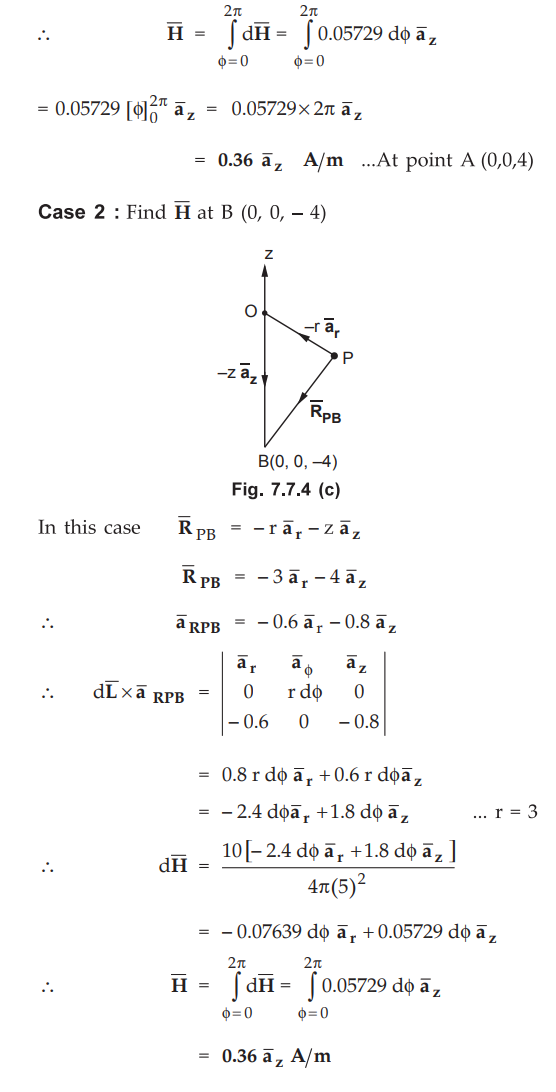
In
the cylindrical co-ordinates,
r
= √x2 + y2 = √9 = 3
Thus
the radius of the circular loop is 3.
Consider
the differential length ![]() at point P on the circular loop. This
at point P on the circular loop. This ![]() is in the plane for which r is constant and z = 0. Thus I
is in the plane for which r is constant and z = 0. Thus I ![]() is
tangential at point P in
is
tangential at point P in ![]() direction.
direction.

Key
Point : Due to the radial symmetry, all the radial (- ![]() )
components at A are going to cancel each other. Hence
)
components at A are going to cancel each other. Hence ![]() exist
only in z direction.
exist
only in z direction.
Thus
at both the points A (0, 0, 4) and B (0, 0, - 4), the ![]() remains same.
remains same.
Examples
for Practice
Ex.
7.7.3 A circular loop located on x2 + y2 = 9,
z = 0 carries a current of 10 A. Determine H at (0, 0, 5) and (0, 0, - 5). Take
the direction of current in
anti-clockwise direction.

Ex.
7.7.4 A thin ring of radius 5 cm is placed on
the plane z = 1 cm, so that its center is at (0, 0, 1 cm). If the ring carries
a direct current of 50 mA along direction, find ![]() at P (0, 0, - 1 cm)
using Biot-Savart’s law.
at P (0, 0, - 1 cm)
using Biot-Savart’s law.
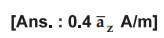
Review Question
1. What is Biot-Savart law 1 Find the magnet flux density at a
point P on the axis of a circular loop of radius 'a' that carries a direct
current I.
AU : Dec.-02, 03. 08, 10, 17, Hay-06, 09, 16, 18. Harks 16
Electromagnetic Theory: Unit III: (a) Magnetostatics : Tag: : - Magnetic field intensity (H) on the Axis of a Circular Loop
Related Topics
Related Subjects
Electromagnetic Theory
EE3301 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
