Magnetic Leakage and Fringing

Magnetic Leakage and Fringing

AU : May-10,15

•  Most of the applications which are using magnetic effects of an electric current, are using flux in air gap for their operation. Such devices are generators, motors, measuring instruments like ammeter, voltmeter etc. Such devices consist of magnetic circuit with an air gap and flux in air gap is used to produce the required effect.     

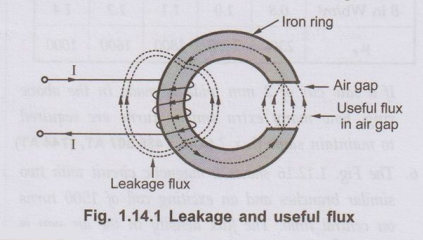
• Such flux which is available in air gap and is utilised to produce the desired effect is called useful flux denoted by ϕ_u

• It is expected that whatever is the flux produced by the magnetizing coil, it should complete its path through the iron and air gap. So all the flux will be available in air gap. In actual practice it is not possible to have entire flux available in air gap. This is because, we have already seen that there is no perfect insulator for the flux. So part of the flux completes its path through the air or medium in which coil and magnetic circuit is placed.

Key Point : Such flux which leaks and completes its path through surrounding air or medium instead of the desired path is called the leakage flux.

The Fig. 1.14.1 shows the useful and leakage flux.

1. Leakage Coefficient or Hopkinson's Coefficient

• The ratio of the total flux (OT) to the useful flux (ou) is defined as the leakage coefficient of Hopkinson's coefficient or leakage factor of that magnetic circuit It is denoted by a  λ.

 ஃ   λ = Total flux / Useful flux = ϕ_T/ϕ_u

•  The value of ‘λ is always greater than 1 as ϕ_T  is always more than ϕ_u. It generally varies between 1.1 and 1.25. Ideally its value should be 1.

2. Magnetic Fringing

• When flux enters into the air gap, it passes through the air gap in terms of parallel flux lines. There exists a force of repulsion between the magnetic lines of force which are parallel and having same direction. Due to this repulsive force there is tendency of the magnetic flux to bulge out (spread out) at the edge of the air gap. This tendency of flux to bulge out at the edges of the air gap is called magnetic fringing.

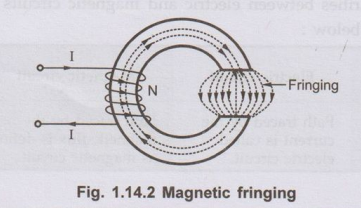
It has following two effects :

1) It increases the effective cross-sectional area of the air gap.                                     

2) It reduces the flux density in the air gap.

So leakage, fringing and reluctance, in practice should be as small as possible.

Key Point : This is possible by choosing good magnetic material and making the air gap as narrow as possible.

• Practically if fringing effect is to be considered then the corrections for short gaps are empirically made by adding one gap length to each of the two dimensions making up its area.

 • Thus if area of core is a_c = l_c × l_c, then the a_g = ( l_c + l_g) × ( l_c + l_g) is the area of cross-section of air gap for considering the effect of fringing. Thus a_g > a_c and the air gap reluctance is less due to fringing.

 • In case of circular cross-section while calculating the area of cross-section for air gap the diameter is considered as (d+2l_g) where l_g is the air gap length and d is the diameter of cross-section of core. This takes into account the effect of fringing.

3. Stacking Factor

• Generally magnetic cores are made up of laminations which are lightly insulated. The laminated construction helps to keep eddy current losses to low value. Due to stacks of laminations, the net cross-sectional area occupied by the magnetic material is less than its gross cross-sectional area. Thus the stacking factor is defined as,

Stacking factor =Net cross - sectional area occupied by magnetic material/Gross cross-sectional area

As gross cross-sectional area is higher, the stacking factor is always less than unity.

Key Point : As the thickness of the laminations increases, the stacking factor approaches to unity.

Ex. 1.14.1 A cast iron ring of 40 cm mean length and circular cross section of 5 cm diameter is wound with a coil. The coil carries a current of 3 A and produces a flux of 3 mWb in the air gap. The length of the air gap is 2 mm. The relative permeability of the cast iron is 800. The leakage coefficient is 1.2. Calculate number of turns of the coil.

Sol. : 

Ex. 1.14.2 The core of an electromagnet is made of an iron rod of 1 cm diameter, bent in to a circle of mean diameter 10 cm, a radial air gap of 1 mm being left between the ends of the rod. Calculate the direct current needed in coil of 2000 turns uniformly spaced around the core to produce a magnetic flux of 0.2 mWb in the air gap. Assume that the relative permeability of the iron is 150, that the magnetic leakage factor is 1.2 and that the air gap is parallel. AU : May-15, Marks 13

 Sol. The ring is shown in the Fig. 1.14.4.

Review Questions

1. Discuss : i) Leakage flux ii) Fringing iii) Stacking factor. AU : May-10, Marks 12

 2. For the magnetic circuit shown in the Fig. 1.14.5, calculate the exciting current required to establish a flux of 2 mWb in the air gap. Take fringing into account empirically

The B-H curve is given in the table.