Magnetic Scalar and Vector Potentials

Magnetic Scalar and Vector Potentials

AU : May-05, 07, 09, 11, 12, 14, I Dec.-02, 09, 11, 12, 17, 18, 19

• In electrostatics, it is seen that there exists a scalar electric potential V which is related to the electric field intensity .

• Is there any scalar potential in magnetostatics related to magnetic field intensity ? 

• In case of magnetic fields there are two types of potentials which can be defined :

1. The scalar magnetic potential denoted as Vm

2. The vector magnetic potential denoted as Ā.

• To define scalar and vector magnetic potentials, let us use two vector identities which are listed as the properties of curl, earlier.

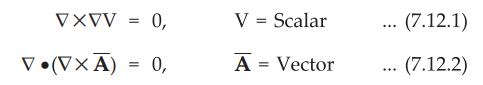
• Every Scalar V and Vector Ā must satisfy these identities.

 

1. Scalar Magnetic Potential

• If V_m is the scalar magnetic potential then it must satisfy the equation (7.12.1),

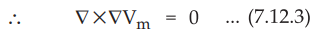
• But the scalar magnetic potential is related to the magnetic field intensity  as,

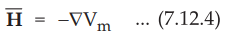
Using in equation (7.12.3),

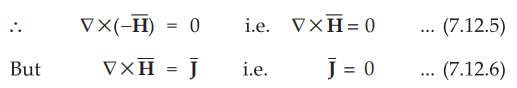
• Thus scalar magnetic potential V_m can be defined for source free region where   i.e. current density is zero.

• Similar to the relation between  and electric scalar potential, magnetic scalar potential can be expressed interms of  as,

 

2. Laplace's Equation for Scalar Magnetic Potential

• It is known that as monopole of magnetic field is non existing,

• This is Laplace's equation for scalar magnetic potential. This is similar to the Laplace's equation for scalar electric potential .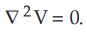

 

3. Vector Magnetic Potential

• The vector magnetic potential is denoted as Ā and measured in Wb/m. It has to satisfy equation (7.12.2) that divergence of a curl of a vector is always zero.

Thus curl of vector magnetic potential is the flux density.

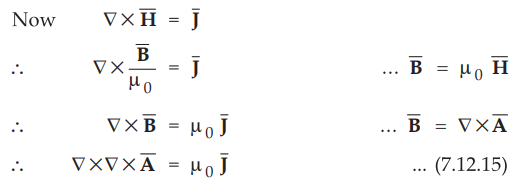
• Using vector identity to express left hand side we can write,

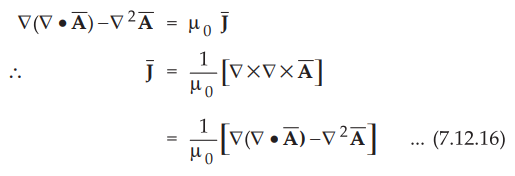
• Thus if vector magnetic potential is known then current density  can be obtained. For defining Ā the current density need not be zero.

 

4. Poisson's Equation for Magnetic Field

• In a vector algebra, a vector can be fully defined if its curl and divergence are defined.

• For a vector magnetic potential Ā, its curl is defined as  which is known.

• But to completely define Ā its divergence must be known. Assume that 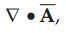 the divergence of Ā is zero. This is consistent with some other conditions to be studied later in time varying magnetic fields. Using in equation (7.12.16),

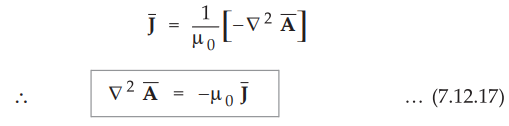
This is the Poisson's equation for magnetostatic fields.

 

5. Ā due to Differential Current Element

Consider the differential element    carrying current I. Then according to Biot-Savart law the vector magnetic potential Ā at a distance R from the differential current element is given by,

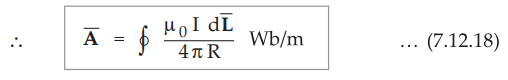
• For the distributed current sources, I can be replaced by  dS where  is surface current density.

• The line integral becomes a surface integral. If the volume current density  is given in A/m2 then Ican be replaced by  dv where dv is differential volume element.

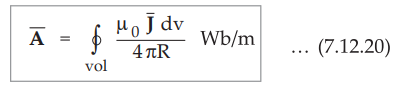
It can be noted that,

1. The zero reference for Ā is at infinity.

2. No finite current can produce the contributions as R → ∞

 

Ex. 7.12.1 Obtain an expression for magnetic vector potential in the region surrounding an infinitely long straight filamentary current I.

AU : May-05, 09, 12, 14, Dec.-02, Marks 16

Sol. : Consider an infinitely long filament carrying direct current I placed along z axis as shown in the Fig. 7.12.1.

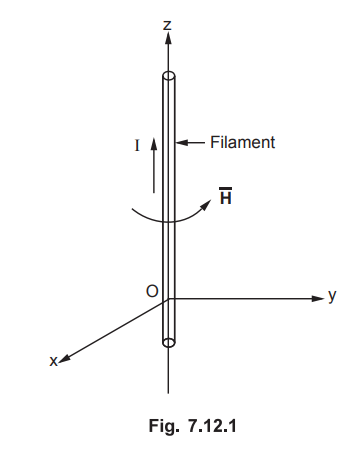
The magnetic field intensity due to such filament is given by,

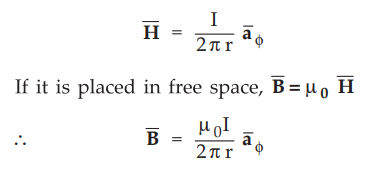
Assuming cylindrical co-ordinate system,

As   is a function of r only, the Ā will also change with r only and will be constant with respect to z.

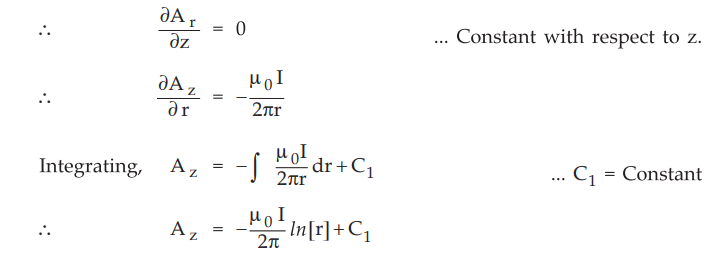
To find C, let us find reference zero where A_z will be zero. Let A_z is zero at r = r0.

 

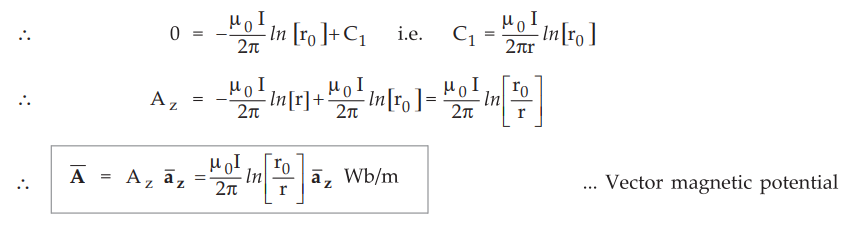
Ex. 7.12.2 In cylindrical co-ordinates 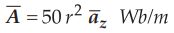 is a vector magnetic potential, in a certain region of free space.

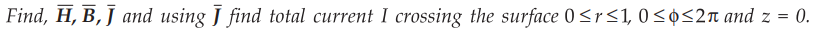
Sol . :

So current is 500 MA and negative sign indicates the direction of current.

 

Ex. 7.12.3 At a point P (x, y, z) the components of vector magnetic potential Ā are given as, Ax = A_x + 3y + 2z, A_y = 5x + 6y+3z and A_z = 2x + 3y + 5z

Determine   at point P and state its nature.

Sol. : The B from vector magnetic potential is given by,

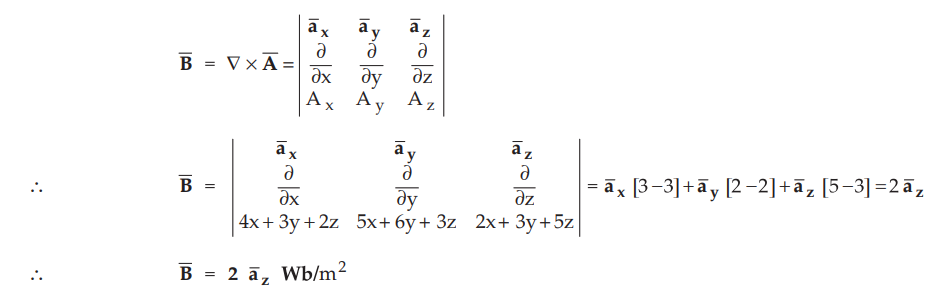
lts magnitude is constant in the direction  . It is a conservative field.

 

Ex. 7.12.5 Derive Biot-Savart’s law and Ampere's law using the concept of magnetic vector potential.

AU : Dec.-12, 18, Marks 10

Sol. :

It is know that for Ā = Vector magnetic potential,

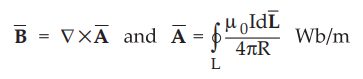
Ā is defined for differential element   as Biot-Savart's law is also defined for differential element  

The equation (6) represents Ampere's circuital law.

 

Examples for Practice

Ex. 7.12.6 If a plane z = 0 carries uniform current

Ex. 7.12.8 A differential current element Idz  is located at the origin in free space.

Obtain the expression for vector magnetic potential due to the current element and hence find the magnetic field intensity at the point (ρ, ϕ, z).

AU : Dec.-11, Marks 8

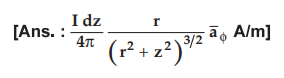
Review Questions

1. Write a note on scalar and vector magnetic potentials.

2. Compare and contrast scalar and vector potentials.

AU : Dec.-17, Marks 4

3. Derive poisson's equation for magnetostatic field.

AU : Dec.-18, Marks 4

4. Deriv vector potential for uniform magnetic field.

AU : Dec.-19, Marks 6