Magnetic Torque and Magnetic Dipole Moment

Magnetic Torque and Magnetic Dipole Moment

AU : Dec.-12,14,17, May-16,17,18,19

• In the previous section we discussed the force on a current loop in a magnetic field. Let us now consider new quantity, magnetic torque.

• The moment of a force or torque about a specified point is defined as the vector product of the moment arm  and the force  It is measured in newton meter (Nm).

• From above expression it is clear that when total force is zero, the torque is independent of the choice of the origin.

1. Torque on a Planar Coil

• Consider a differential current loop of rectangular shape with uniform magnetic field everywhere around it as shown in the Fig. 8.5.3. Assume that the loop is placed in xy-plane. Let the sides AB and CD be parallel to x-axis and sides BC and DA be parallel to y-axis. Let dx and dy be the lengths of the sides of the rectangular loop.

 • Considering origin of the rectangular co-ordinate system as the centre of the loop. The value of the magnetic field at the centre of the rectangular loop carrying current I in anticlockwise direction be BQ. As the rectangular loop is differential with the differential lengths dx and dy, the value of the magnetic field can be assumed BQ everywhere. The total force on the loop is zero and the origin for the torque can be selected as the centre of the loop.

The force exerted on side AB is given by,

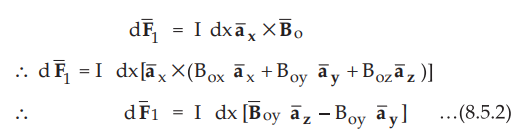
For the side AB, the level arm extends from origin to the midpoint of the side AB. Thus the lever arm for side AB is given by,

 ...(8.5.3)

Hence the torque on side 1 is given by,

• For the side BC, the lever arm extends from origin to the midpoint of the side BC. Thus the lever arm for side BC is given by,

• For side CD, the torque contribution is exactly same as that by side AB. The torque on side 3 is given by,

• Similarly for DA, the torque contribution is exactly same as that by side BC. The torque on side 4 is thus given by,

• Hence the total torque is given by,

• We can modify above equation by replacing the product term i.e. dx dy by vector area of the differential current loop i.e. 

• Above equation indicates that even though the total force exerted on the rectangular loop as a whole is zero, the torque exists along the axis of rotation, i.e. in the z-direction. The expression is valid for all the flat loops of any arbitrary shape.

2. Magnetic Dipole Moment

• The magnetic dipole moment of a current loop is defined as the product of current through the loop and the area of the loop, directed normal to the current loop. From the definition it is clear that, the magnetic dipole moment is a vector quantity. It is denoted by. The direction of the magnetic dipole moment  is given by the right hand thumb rule. The right hand thumb indicates the direction of the unit vector in which  is directed and the figures represents the current direction. The magnetic dipole moment is given by,

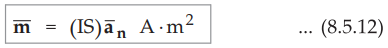
• In the previous section we have obtained the expression for the torque along the axis of rotation of a planar coil as,

• Using definition for the magnetic dipole moment, the torque can be expressed as,

• Above expression is in general applicable in calculating the overall torque on a planar loop of any arbitrary shape. But the basic requirement is that the magnetic field must be uniform. The torque is always in the direction of axis of rotation. When the planar loop or coil is normal to the magnetic field, the sum of the forces on the planar loop as well as the torque will be zero.

3. Magnetic Dipole

• A magnetic dipole is nothing but a bar magnet or the filamentary current loop. Consider small filamentary loop carrying current I as shown in the Fig. 8.5.4.

• Let the infinitesimal current element be  carrying current I. The point P is at a distance r from the loop of radius a. Assume that distance r between loop and point of observation to be very large as campared to the radius of loop i.e. a.

• The vector magnetic potential at point P differential current element is given by,

• As per the assumption r >> a, the loop appears very small at point P. Such that, Ā has only ϕ component,

It is called magnetic moment of the loop.

• It is observed that the expressions obtained for Ā and  are very much similar to those obtained for V and  in case of electric dipole. Thus we can consider a small current loop as a magnetic dipole.

• The  lines are shown around the small current loop i.e a magnetic dipole . It is also observed that the  lines due to a bar magnet are very similar to the  lines due to a small current loop. The  lines due to a bar magnet are a shown in the Fig. 8.5.5 (b). Suppose Q_m is the isolated magnetic charge which exists in association with - Qm always. When a bar of length I is placed in a uniform magnetic field , a torque is produced on bar given by,

• Note that the direction of  is always from south to north as represented in Fig. 8.5.5 (b).

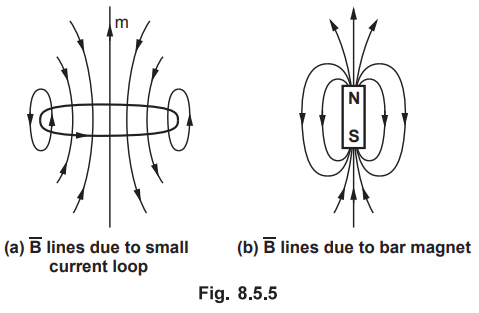
This torque produced aligns the bar with an external magnetic field. So the force acting on the charge is given by,

• Suppose in a given field , the torque produced by a small current loop and a bar magnet is same, then they are equivalent of each other.

• Equation (8.5.19) represents the condition that the dipole moment of a small current loop and a bar magnet must be same if they produce same torque in an uniform magnetic field .

Ex. 8.5.1 Find the magnetic field due to a small circular loop of radius a carrying current I, at a distance R from the loop. R is very large as compared to dimensions of the loop as show in the Fig. 8.5.6.

Sol. : According to Biot-Savart law, the vector magnetic potential Ā at a distance r. From the differential current element dL carrying current I is given by,

It is given that distance R is very large compared to the radius of loop a (r >> a), then from the point P, the loop appears to be very small and Ā has only ϕ component. Thus we can write,

Now the magnetic flux density is given by, 

Ex. 8.5.2 A circular loop of radius r and current I lies in z = 0 plane. Find the torque which results if the current is in  and there is a uniform field 

Sol. : Consider a circular loop in z = 0 plane as shown in the Fig. 8.5.7.

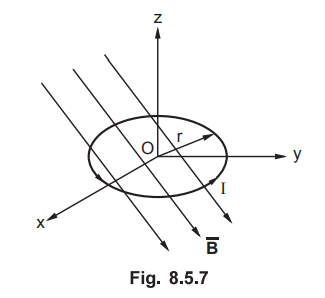
Current is in  as shown in the Fig. 8.5.7. The given magnetic field is uniform given by

The magnetic dipole moment of a planar circular loop is given by,

where S is the area of the circular loop.

Note that the loop is laying in z = 0 plane. Thus the direction of unit normal  must be decided by the right hand thumb rule. Let the fingures point in the direction of current (in  direction), then the right thumb gives the direction of  which is clearly  .

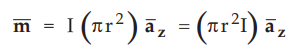
The total torque is given by 

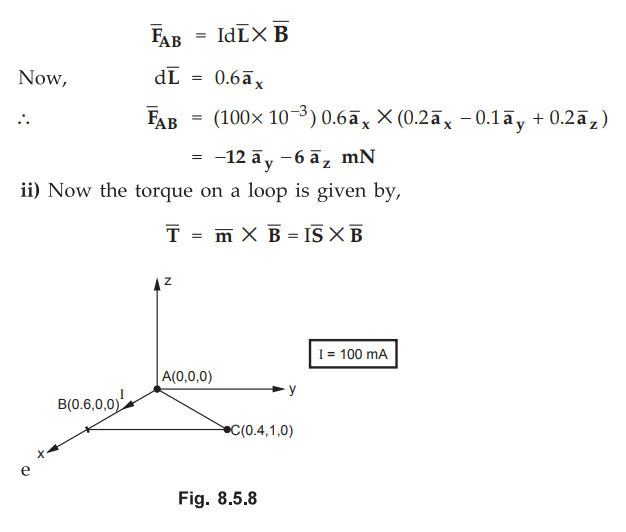
Ex. 8.5.3 A loop wire is bent in the form of triangle as shown in the Fig. 8.5.8. A current of 100 mA flows in ā_x direction in the segment AB. If the uniform magnetic field is   = 0.2ā_x − 0.1āу +0.2ā2 T find,

i) Force on segment AB ii) Torque on the loop if origin at (0, 0, 0).

Sol. : Given

I = 100 mA = 100 × 10^-3 A,  = 0.2ā_x - 0.1ā_y +0.2ā_z T

i) The force exerted on segment AB is given by,

Now area of triangle shaped loop placed in x-y plane can be written in vector form as,

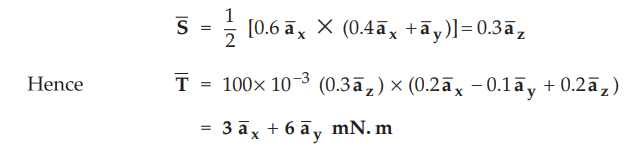
Ex. 8.5.4 What is the maximum torque on a square loop of 1000 turns in a field of uniform flux density B Tesla ? The loop has 10 cm sides and carries a current of 3 A. What is the magnetic moment of the loop ?

Sol. : The area of a single turn of a square loop of sides 10 cm is given by,

S' = (l0 × l0^-2)(l0 × l0^-2) = 0.01m²

Hence for 1000 turn square loop, the total area is given by,

S = NS' = (1000) (0.01) = 10 m²       ... N = Number of turns

The magnitude of the magnetic dipole moment is given by,

m = I S = (3) (10) = 30 A• m²

Hence the magnitude of the maximum torque is given by,

T_max = mB = 30 B N • m

Ex. 8.5.5 Find the torque about the y-axis for the two conductors of length I, separated by a distance in the uniform field   as shown in the Fig. 8.5.9.

Sol. : Both the conductors are of same length I and are separated by a fixed distance W. The force  , experienced by a conductor to the left of origin is given by,

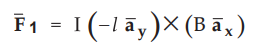
Note that, from the Fig. 8.5.9,   is uniform along + x direction.

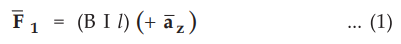
The force, , experienced by a conductor to the right of the origin is given by,

The moment arm of a force  from the left conductor is given by,

Similarly the moment arm of a force  from the right conductor is given by,

Thus the total torque from the left conductor and the right conductor is given by,

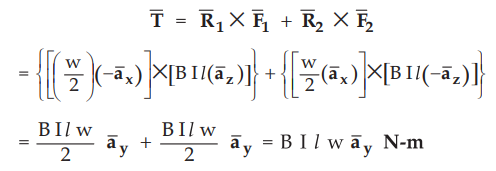
Ex. 8.5.6 Find the maximum torque on an 85 turn rectangular coil, 0.2 m by 0.3 m carrying current of 2 A in a field B = 6.5 T.

Sol. : The area of single turn rectangular coil is given by,

S₁ = (0.2) (0.3) = 0.06 m²

Hence for 85 turns of rectangular coil, the total area is given by,

S = NS₁ = (85) (0.06) = 5.1 m²

The magnitude of the magnetic dipole moment is given by,

m = IS = (2) (5.1) = 10.2 A.m²

AU : Dec.-14, Marks 8

Hence the magnitude of the maximum torque is given by,

T_max = mB = (10-2) (6’5) = 663 Nm

Examples for Practice

Ex. 8.5.7 A small current loop with magnetic moment 5A-m² is located at the origin. While another small current loop L2 with magnetic moment 3A-m² is located at (4, - 3, 10). Determine the torque on L2.

Ex. 8.5.8 A current of 6 A flows from M(2, 0, 5) to N(5, 0, 5) in a straight solid conductor in free space. An infinite current filament lies along z-axis and carries 50 A current in   direction. Compute vector torque on the wire segment using an origin at (3, 0, 0).

Review Questions

1. Derive an expression for torque on a rectangular loop carrying current I and is situated in uniform magnetic field B Wb/m² .

2. Define dipole and electromagnetic fields.

3. What is magnetic torque

4. Find an expression for ti loop carrying a currentl.

AU : Dec.-14, Marks 8

5. Find the magnetic field intensity at point P (1.5, 2, 3) caused by a current filament of 24 ampere in the az direction on the z axis and extending from z = 0 to z = 6.

AU : May-16, Marks 8

6. Determine the torque on a rectangular loop (a m × b m) carrying current I and placed in a uniform magnetic field.

AU : May-16, Marks 8