Magnetization and Permeability

Magnetization and Permeability

AU : Dec.-05, May-10, 18

• We have already studied that in any magnetic material, the electrons revolve in the orbits around the positive central nucleus. Simultaneously the electrons also rotate or spin about their own axes.

• The movement of the orbital electrons, electron spin and nuclear spin produce internal magnetic field similar to that produced by current loop. The current produced by the bound charges (orbital electrons, electron spin, nuclear spin) is called bound current represented by Ib. The bound charges are charges which are bound to nucleus. (The current by free charges is called free current.) The field produced due to movement of bound charges is called magnetization represented by . There is a dimensional equivalence between  and . Generally it is represented in terms of the magnetic dipole moment .

• Let the bound current Ib flows through a closed path. Assume that this closed path encloses a differential area  Then the magnetic dipole moment is given by

• Now consider a differential volume AV. Assume that there are n magnetic dipoles per unit volume. The total magnetic dipole moment can be obtained summing up all the individual magnetic dipole moment of each magnetic dipole. Note  that, we must add all these moment vectorically

• The magnetization is defined as the magnetic dipole moment per unit volume. Its unit is A/m.

• Consider a differential volume When external field is not applied to the material, there is random orientation of the magnetic dipole moments as shown in the Fig. 8.7.2 (a). Thus the total sum of the magnetic dipole moments is zero. Thus the magnetization  is also zero. With the application of an external field , the magnetic moments of electrons tend to align with  on there own such that net magnetic moment is not equal to zero. Refer Fig. 8.7.2 (b).

• Let us consider alignment of a magnetic dipole along a closed path as shown in the Fig. 8.7.3.

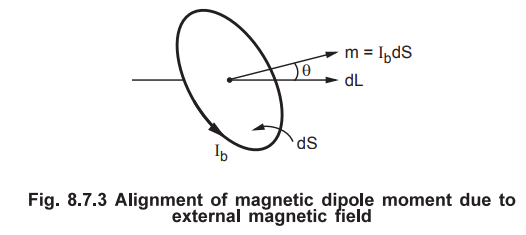
• From above representation it is clear that the magnetic moment  makes angle θ with the element of the closed path . Thus its component along the direction of dL is nothing but the projection of  on  The magnetic dipole moment is perpendicular to the surface area dS. To obtain magnetic moment making angle θ° with dL, it is necessary to consider differential volume defined by differential surface area dS and component of dL in the direction of magnetic moment. Thus differential volume can be defined as dS dL cos 0 and according to definition of the dot product, it is expressed as . But in this small volume there are n total magnetic moments. Under the external magnetic field, random orientiation changes to partial alignment of the magnetic moments. To achieve this the bound current increases by I_b for each magnetic dipole. Hence we can write,

• Basically  is nothing but magnetic dipole moment multiplied by number of magnetic dipoles per unit volume gives magnetization. The increase in current for part of the closed path is represented by equation (8.7.4). Actually there are large number of magnetic moments along a closed path. Thus the total increase in current can be obtained by integrating equation (8.7.4) over a closed path.

• The total current is the summation of bound current (Ib) and free current (I). Note that the free current is due to the free electrons i.e. it is conventional current.

• Writing Ampere circuital law for the total current I_T,

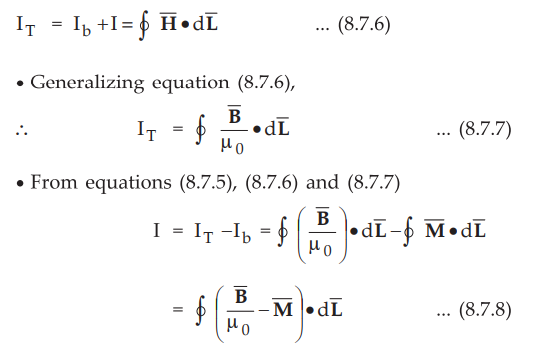
• Compare this equation with the expression of Ampere's circuital law given by,

• The relationship in equation (8.7.10) is true for all the materials irrespective of the nature of material whether it is linear or not.

• For linear, isotropic magnetic materials,

• The quantity X_m is dimensionless and is called magnetic susceptibility of the medium. Thus the magnetic susceptibility measures how susceptible the material is to a magnetic field.

• Substituting value of , from equation (8.7.11), in equation (8.7.10),

• But for any magnetic material we can write

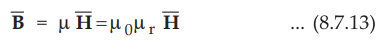
• Comparing equations (8.7.12) and (8.7.13), the relative permeability can be expressed interms of magnetic susceptibility as

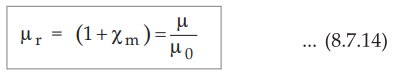
• In general µ = µ₀µ_r is called permeability of a material. It is measured in henry/meter (H/m). But the relative permeability is a dimensionless quantity similar to the magnetic susceptibility.

• Consider again the expressions for the currents. These currents can be expressed interms of the current densities. Let  be the total current density,  be the bound current density and be the free current density. Then we can write the expressions for currents as,

From the curl definition we can write,

• Equation (8.7.15) is nothing but the point form of Ampere's circuital law.

Ex. 8.7.1 Find the magnetic field intensity within a magnetic material where

a) M = 150 Aim and µ = 1.5 × 10^-5 Hm

b) B = 300 µT and Xm = 15

c) There are 8.2 × 10²⁸ atoms/m³, each atom has a dipole moment of 5 × 10^-27 Am² and µr = 30.

Sol. : a) The relative permeability µr can be obtained as,

The magnetic field intensity and the magnetization are related to each other as,

M = Xm H = (µr -1) H

The magnetic field intensity thus can be obtained as,

H = M / µr – 1 = 150 / 11.9366 – 1 = 13.7154 A/m

b) The magnetic flux density is given by,

Ex. 8.7.2 In certain region, the magnetic flux density in a magnetic material with Xm = 6 is given as . At y = 0.4 m, find the magnitude of;

Sol. :

Examples for Practice

Ex. 8.7.3 Find the permeability of the material whose magnetic susceptibility is 49.

[Ans. : 31.4159 × 10^-6 H / m]

Review Questions

1. What is magnetization

2. Define the terms : magnetic permeability.

3. Explain magnetization in magnetic materials and explain how the effect of magnetization is taken into account in the calculation of B/H.

AU : Dec.-05, Marks 10