Maxwell's First Equation

Maxwell's First Equation

• The divergence of electric flux density  is given by,

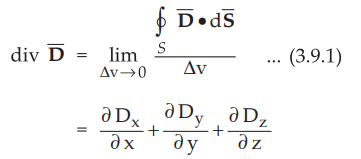
According to Gauss's law, it is known that

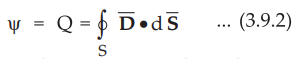
Expressing Gauss's law per unit volume basis

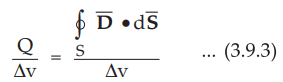
Taking lim Δv → 0 i.e. volume shrinks to zero,

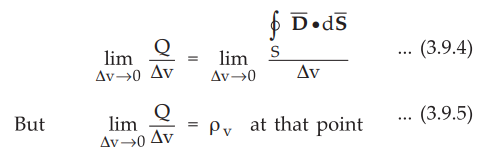
• The equation (3.9.5) gives the volume charge density at the point where divergence is obtained.

• Equating equations (3.9.1) and (3.9.5),

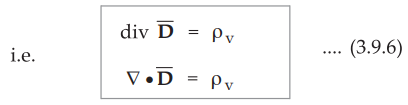
• This is volume charge density around a point. The equation (3.9.6) is called Maxwell's first equation applied to electrostatics. This is also called the point form of Gauss's law or Gauss's law in differential form.

The statement of Gauss’s law in point form is,

The divergence of electric flux density in a medium at a point (differential volume shrinking to zero), is equal to the volume charge density (charge per unit volume) at the same point.

Ex. 3.9.2 Prove that the divergence of the electric field and that of electric flux density in a charge free region is zero.

Sol. : From point form of Gauss's law we can write,