Mesh current method

MESH CURRENT METHOD

In mesh method, Kirchhoff's Voltage Law (KVL) is applied to a network. For this network, we have to write mesh equations interms of mesh currents. Here, we are using mesh currents instead of branch currents.

Here, each mesh is assigned a separate mesh current. Assume that the mesh current direction is clockwise. Then, KVL is applied to the network, in order to write equations interms of unknown mesh currents.

The branch current can be found out by taking the algebraic sum of the mesh currents which are common to that branch.

The following steps should be implemented to find out the mesh current and branch currents.

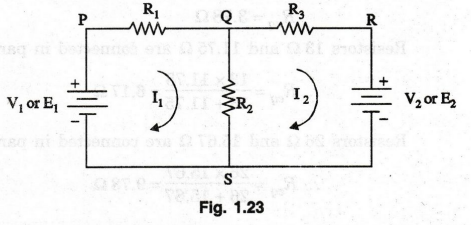
Consider a simple network as shown in figure 1.23.

Step 1: First, each mesh is assigned a separate mesh currents. Assume all mesh currents directions are clockwise. Consider the figure 1.23. It consists of two meshes (PQSP and QRSQ and two mesh currents (I₁ and I₂).

Step 2: If two mesh currents (I₁ and I₂) are flowing through a network element, the actual current in the circuit element is the algebraic sum of the two (I₁ and I₂). In this network, mesh currents, I₁ and I₂ are flowing through R₂. First, we consider one direction i.e. Q to S, current is I₁- I₂ and if go for another direction. i.e., S to Q, current is I₁ – I₂

Step 3: Write equation for each mesh in terms of mesh currents by applying KVL. When writing mesh equations, we assign rise in potential as positive (+) sign and fall in potential as negative (-) sign.

Step 4: Suppose any value of mesh current becomes negative in the solution, the actual or true direction of the mesh current is anticlockwise, i.e., opposite to the clockwise direction. 00

By applying KVL to the figure 1.23, we get two equations

Mesh PQSP

- I₁ R₁ – (I₁ – I₂ ) R₂ + V₁ = 0

 (or) I₁ (R₁ + R₂ ) – I₂ R₂ = V₁    ...(39)

Mesh QRSQ

- I₂ R₃ – V₂ (I₂ – I₁ ) R₂ = 0

 (or) + I₁ R₂ – I₂ (R₂ + R₃ ) = V₂    ...(39)

The mesh currents I, and I2 can be found out by solving equations (39) and (40).

Step 5: The branch currents can be easily found out by using the mesh currents I₁ and I₂.

EXAMPLE 85: Solve the mesh and branch currents shown in figure.

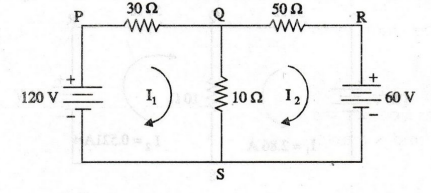
Solution :

First assign mesh currents I₁ and I₂ to meshes PQSP and QRSQ respectively. It is shown in figure.

Mesh PQSP

-30 I₁ -10 (I₁- I₂) + 120 = 0

40 I₁ -10 I₂ = 120   …… (1)

Mesh QRSQ

-50 I₂ – 60 - 10 (I₂ – I₁) = 0

-10 I₁  + 60 I₂ = - 60   ……. (2)

The two equations are

40 I₁ -10 I₂ = 120    ...... (1)

- 10 I₁ + 60 I₂  = -60  ……. (2)

Multiplying equation (2) by 4 and adding it to equation (1)

40 I₁ -10 I₂  = 120

- 40 I₁  + 240 I₂ = -240

Solving these two equations, we can get

I₂ = - 0.521 A

The negative sign indicates that the direction of I2 is anticlockwise. Substituting I2 value in equation (1) we get,

40 I₁ -10 (-0.521) = 120

I₁ = 114.79 / 40

I₁ =  2.86 A

The actual direction of flow of mesh currents is shown in figure.

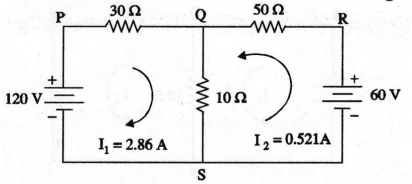
The mesh current I₁ = 2.86 A

I₂ = 0.521 A

Current in branch SPQ, I₁ = 2.86 A

Current in branch SRQ, I₂ = 0.521 A

Current in branch QS= I₁ + I₂

= 2.86 + 0.521 = 3.381 A

1.97

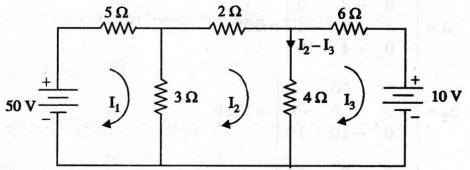
EXAMPLE 86: Determine the power dissipation in the 4 2 resistor of the circuit show in figure.

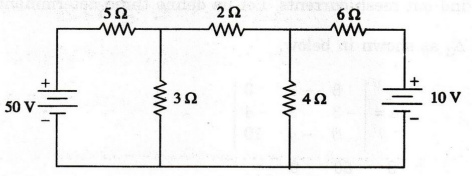
Solution:

First, we should mark the current direction in the given network. It is shown in the following figure.

Let us assume the three mesh currents I₁, I₂ and I₃ as shown in figure. Now, the current flow through 4Ω resistor is I₁ – I₃ in the direction shown in figure.

Mesh equation I

-5 I₁-3 (I₁ – I₂) + 50 = 0

8 I₁ - 3 I₂ = 50 …. (1)

Mesh equation II

-2 I₂ -4 (I₂ – I₃) - 3 (I₂ – I₁) = 0

-3 I₁ + 9 I₂ - 4 I₃ = 0   ...(2)

Mesh equation III

-6 I₃ – 10 - 4 (I₃ - I₂) = 0

- 4 I₂ + 10 I_s = - 10 …… (3)

Matrix representation of (1), (2) & (3)

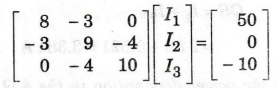
Here, we have to solve the mesh currents I2 and Ig. By applying Cramer's rule, we can easily find out mesh currents. Let us define three determinants.

Δ Δ₂ and Δ₃ as shown in below.

Power dissipated in the 4 Ω resistor

= | I₂ – I₃ |² × 4

= [2.35 - (-0.05976)]² × 4

= 23.22 W

EXAMPLE 87: Use mesh analysis to determine the three mesh currents in the circuit of figure shown in below.

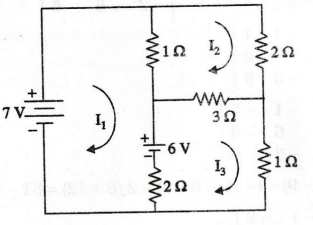
Solution :

The three required mesh currents are assigned as shown in figure. Applying KVL, we can get three mesh equations.

Mesh equation I

Here, we have to solve the mesh currents 11, 12 and 13, by applying Cramer's rule. Let us define three determinants,

Δ, Δ₁, Δ₂ and Δ₃ as shown below.

The three mesh currents are

I₁ = 3A; I₂ = 2A ; I₃ = 3A

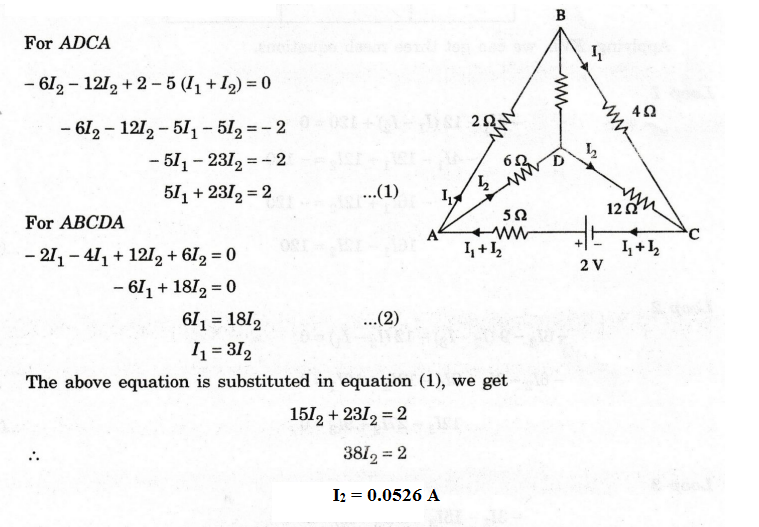
EXAMPLE 88: Determine the value of current through the branch DC of the network shown below in figure, when the current through the branch BD is zero.

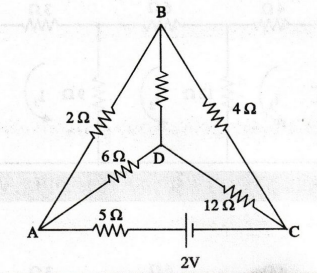
Solution :

We have marked in AB as I₁ and AD is I₂. Since there is no current in BD, I₁ flows through BC and I₂ through DC.

For ADCA

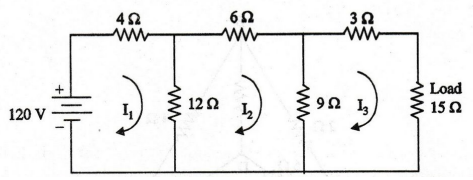
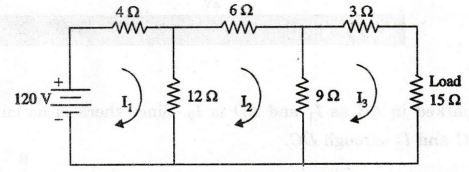
EXAMPLE 89: In the circuit given in figure, obtain the load current and power delivered to the load.

Solution:

Applying, KVL, we can get three mesh equations.

By applying Cramer's rule, we can find out current through load (15Ω). Mesh current I₃ flows through 15 Ω resistor

Current through load resistor (15 Ω) is 2A

Power delivered to the load = I²R = 2² × 15 = 60 W

EXAMPLE 90: Determine the current through 800 2 resistor in the network shown in figure.

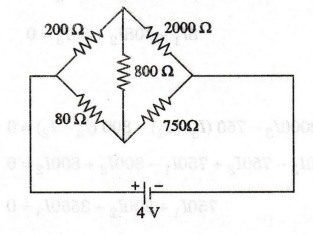
Solution

First we should mark the current direction in this network. It is shown in figure.

Applying KVL, we can get three mesh equations.

By applying Cramer's rule, we can find out current through 800 Ω.

Current through 800 = I₂ – I₃ = 0.00183-0.00181 = 0.00002 A

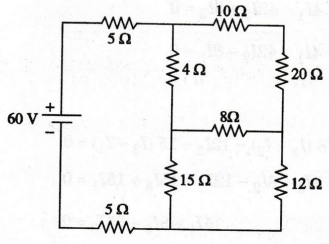
EXAMPLE 91: In the network of figure, find the current delivered by the battery.

Solution :

The three required mesh currents are assigned as shown in figure.

Applying KVL, we can get three mesh equations.

Loop 1

By applying Cramer's rule, we can find mesh current I1 i.e., current delivered by the battery.

currrent delivered by the battery = 2.83 A

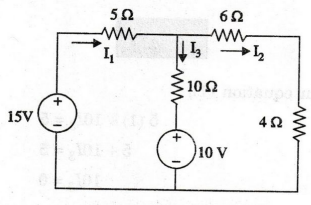
EXAMPLE 92: For the circuit in figure, find the branch currents I1, 12 and 13 using mesh analysis.

Solution :

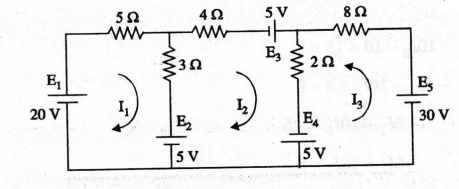
EXAMPLE 93: Determine the current supplied by each battery in the circuit shown in figure using mesh analysis.

Solution :

The three loop currents are shown in figure.

Loop 1

Here we have to solve the mesh currents I₁, I₂ and I₃ by applying Cramer's rule.

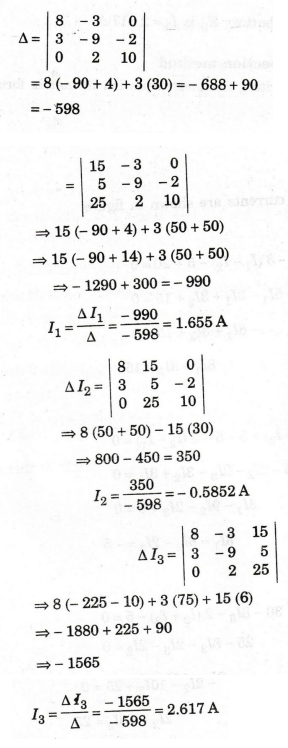
Current supplied by battery E₁ is I₁ = 1.655 A

Current supplied by battery E₂ is I₁ – I₂ = 1.655 – (-0.5852) = 2.2402A

Current supplied by battery E₃ is I₂ = - 0.5852 A

Current supplied by battery E₄ is I₃ + I₂  = 2.617 – 0.5852 = 2.0318 A

Current supplied by battery E₅ is I₃ = 2.617 A

Mesh equations by inspection method

The procedure for writing the mesh equation in matrix from can be simplified as follows.

Steps

1. Convert the current source into voltage source by source transformation.

2. All the resistance through which the loop current I₁ flows are summed and denoted by R₁₁. It is called self resistance of loop 1.

3. All the resistance through which loop currents I₁ in the first loop and I₂ in the second loop flow are summed up. This is denoted by R₁₂. The sign of the term R12 is negative if the two currents I₁ and I₂ through R12 are in opposite directions; otherwise the sign is positive.

4. Let V₁ be the effective voltage on the first loop through which the loop current I₁ flows. The sign of V₁ is positive if the direction of V₁ is same as that of I₁ (i.e aiding the current I₁ otherwise the sign of V₁ is negative). V₁ is written on the right hand side of the equation.

Now, zero is written on the right hand side if there is no source in the first loop through which I₁ flows.

The general matrix form of mesh equation is

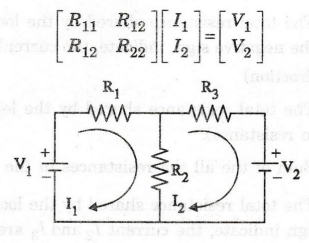
Example 1

Here the circuit consists of two loops.

R₁₁ = R₁+ R₂ (Sum of the all resistances in the 1st loop)

R₂₁ = R₁₂ = -R₂ (The total resistance shared by the loops one and two. Negative sign indicates, the current I₁ and I₂ are in opposite direction)

R₂₂ = R₂ + R₃  (Sum of the all the resistances in the 2nd loop)

First loop voltage source is V₁.

Second loop voltage source is - V₂.

 (The minus sign indicates the loop current I2 flows from the voltage terminal + to −)

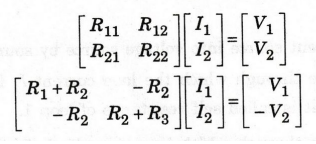
By using Cramer's rule, we can find mesh or loop currents I₁ and I₂.

Example 2

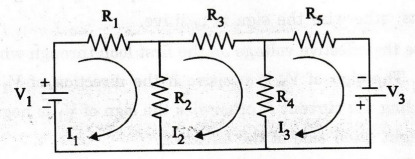
Here, the circuit consists of three loops. So we have to form 3 × 3 matrix.

R₁₁ = R₁+ R₂ (Sum of the all the resistances in the 1st loop)

R₁₂ = R₂₁ = -R₂  (The total resistance shared by the loops one and two. The negative sign, indicate, the current I₁ and I₂ are in opposite direction)

R₁₃ = R₃₁ = 0 (The total resistance shared by the loops one and three. Here, no resistance).

R₂₂ = R₂ + R₃ + R₄ (Sum of the all the resistances in the 2nd loop)

R₂₃ = R₃₂ = -R₄ (The total resistance shared by the loops 2 and 3. The negative sign indicate, the current I, and I are in opposite direction).

R₃₃ = R₄ + R₅  (Sum of the all the resistances in the 3rd loop)

Voltage source in the 1st loop is V₁. (Here the V₁ is positive sign. Because, the loop current I₁ flows from voltage terminal - to +).

Voltage source in the 2nd loop is zero (V₂ = 0).

Voltage source in the 3rd loop is V₃

(Here, the V₃ is positive sign. Because the loop current I_S flows from voltage terminal to +).

Now, the matrix form is

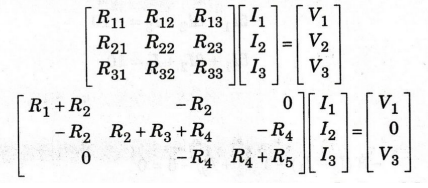
By using Cramer's rule, we can find mesh currents I₁, I₂ and I₃.

EXAMPLE 94: Find the current I₃ using mesh analysis.

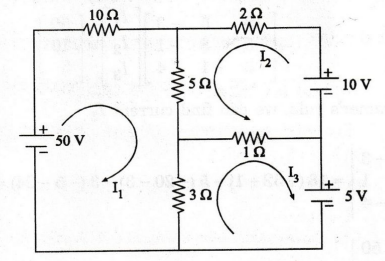
Solution :

There are three loop currents in the above figure.

EXAMPLE 95: In the circuit shown in figure, use mesh analysis to find out the power delivered to the 4 Ω resistor. To what voltage should the 100 V battery be changed so that no power is delivered to the 4 Ω resistor?

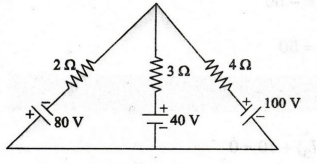
Solution :

By using matrix inspection method

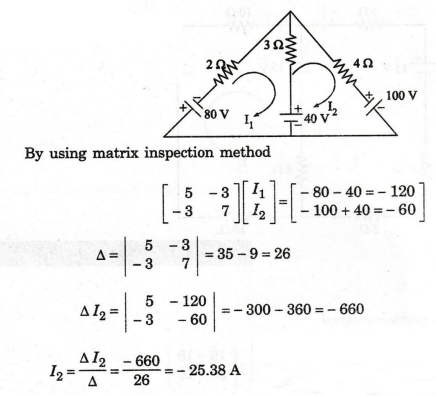
The negative sign indicates that the direction of I₂ is anticlockwise.

I₂ = 25.38 A

Power delivered to the 4 Ω -I²₂ R = 25.83² × 4

= 2576.57 W

No power is delivered to the 4 Ω resistor when ΔI₂ = 0

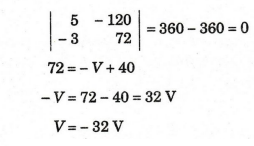
Now the 100 V battery is changed into 32 V

EXAMPLE 96: Find the current through the 8 resistor shown in figure.

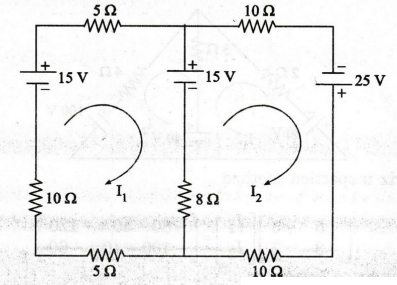
Solution :

EXAMPLE 97: Determine the currents in bridge circuit by using mesh analysis in the figure. (AU, Trichy/EEE - June 2009)

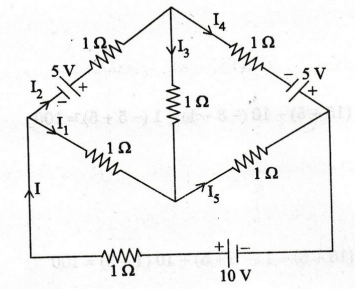
Solution :

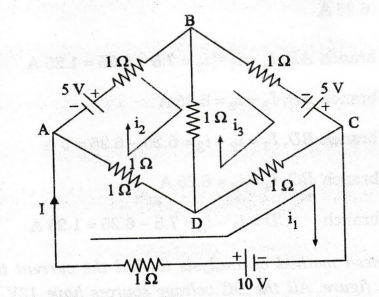
By using mesh inspection method

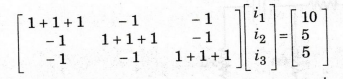
By applying Cramer's rule, we can find out mesh currents i₁, i₂ and i₃.

Current through branch AD, I₁  = i₁ – i₂ = 7.5 - 6.25 = 1.25 A

Current through branch AB, I₂ = i₂ = 6.25 A

Current through branch BD, I₃ = i₂ – i₃ = 6.25 – 6.25 = 0 A

Current through branch BC, I₄ = i₃ = 6.25 A

Current through branch CD = i₁ – i₃ = 7.5 - 6.25 = 1.25 A

EXAMPLE 98: Use mesh method of analysis to find the current through 4 Ω resistor in the circuit shown in figure. All the DC voltage sources have 12V output.

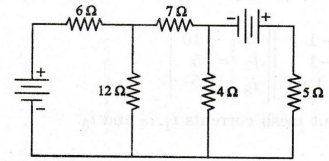
Solution :

By applying mesh inspection method

By applying Cramer's rule, we find out the current through 4 Ω resistor.

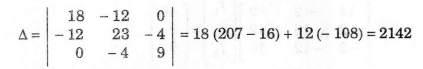
Current through 4 Ω resistor = I₃ - I₂

Current through 4Ω resistor = I₃ – I₂ = 1.78-1.008 = 0.772 A

EXAMPLE 99: For the circuit shown in figure, find the current flowing through the 10 Ω resistor.

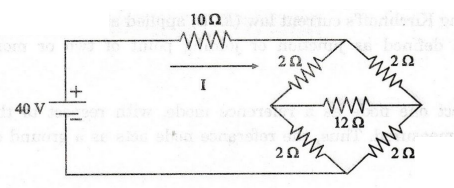
Solution :

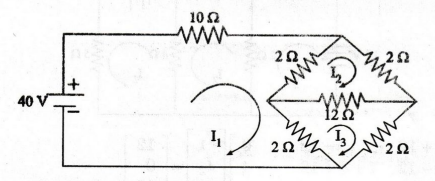
By applying mesh inspection method

Current through 10 Ω resistor is 3.33 A