Method of Images

Method of Images

AU : Dec.-06, June-08, May-11

• The method of images is introduced by Lord Kelvin in 1848. The method is suitable to determine 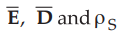 due to the charges in the presence ofcon ductors. The conductors carry the charge only on the surface and surface is an equipotential surface. The method of images helps us to find  and ρS due to the charges in the presence of conducting planes which are equipotential, without solving Poisson's or Laplace's equations.

1. The Image Theory

• Consider a dipole field. The plane exists midway between the two charges, is a zero potential infinite plane. Such a plane may be represented by very thin conducting plane which is infinite. The conductor is an equipotential surface at a potential V = 0 and  is only normal to the surface. Thus if out of dipole, only positive charge is considered above a conducting plane then fields at all points in upper half of plane are same. In other words, if there is a charge above a conducting plane then same fields at the points above the plane can be obtained by replacing conducting plane by equipotential surface and an image of the charge at a symmetrical location below the plane. Such an image is negative of the original charge.

• The images of variouls charge distributions are shown in the Fig. 4.15.1 (b). Where the conducting plane in the Fig. 4.15.1 (a) is replaced by an equipotential surface with V = 0. The charges may be point, line or volume charges.

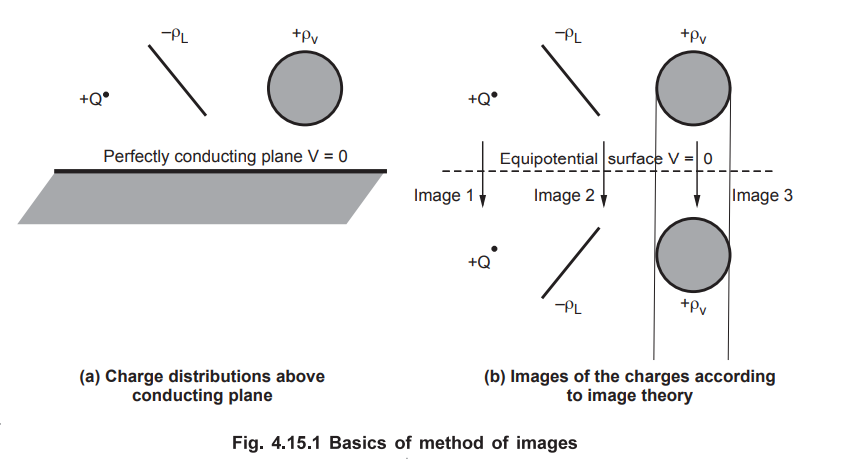
The conditions to be satisfied to apply the method of images are,

1. The image charges must be located in the conducting region.

2. The image charges must be located such that on the conducting surface the potential is zero or constant.

The first condition is to satisfy Poisson's equation, while the other to satisfy the boundary conditions.

2. Method of Images for Point Charges

• Consider a perfect conducting plane in xy plane, infinite in nature. The point charge + Q is located at z = h, above the plane. It is required to obtain  at any point above the plane. Then replace the plane by the equipotential surface and get the image of Q, below the plane. The image charge is - Q, located at z = - h. The original charge and plane are shown in the Fig. 4.15.2 (a) while the image is shown in the Fig. 4.15.2 (b).

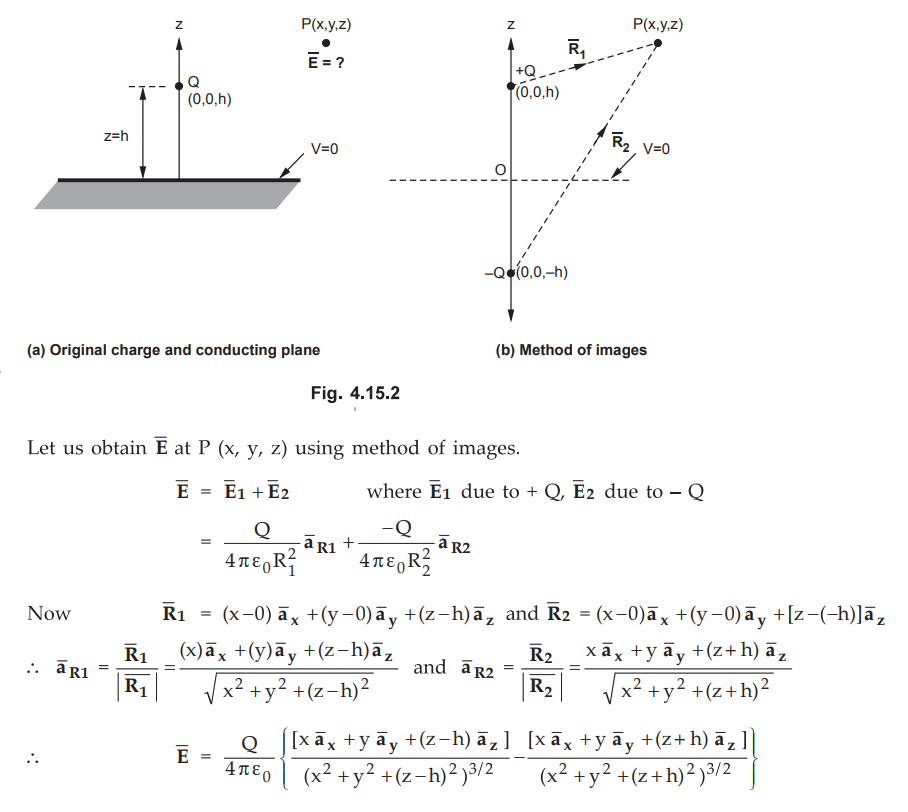
It can be seen that if z = 0 then  has only the Z component. This confirms that E is always normal to the conducting surface.

Let us obtain potential at P (x, y, z). The potential due to the point charge is given by,

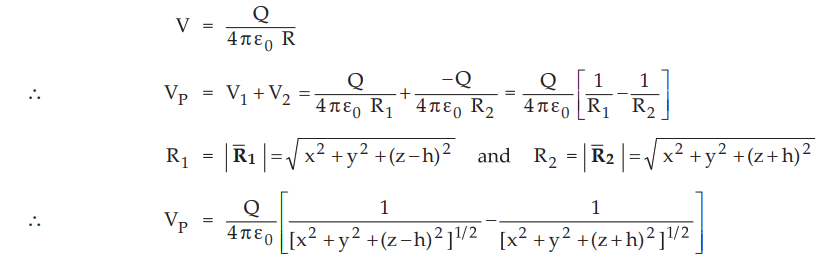
At z = 0, Vp = 0 V which confirms that surface of the conductor is equipotential surface with V = 0.

Similarly other parameters such as ρs = DN which is Ɛ0EN and EN is  with z=0, can be obtained.

The total charge induced on the conducting surface also can be obtained from Gauss's law.

Ex. 4.15.1 Two equal point charges are placed on a line at a distance 'a' apart, this line joining the charges is parallel to the surface of an infinite conducting region which is at zero potential. The specified line is at a distance a/2 from the surface of the conducting region. Show that the force between the charges in 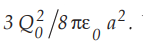 one of the charges is reversed ?

Sol. : Use method of images for this case. According to this method, consider the images of the two charges in the conducting region, having negative sign.  

Let the charge at A and B be Q₀ each.

The image of A is A' and of B is B', with a charge of - Q₀ each.

Total force on A = Force due to Q₀ at B + Force due to – Q₀ at A' + Force due to- Q₀ at B'

Let us find two components, horizontal and vertical of this force.

Example for Practice

Ex. 4.15.2 A point charge of 25 nC located in free space at P (2, - 3, 5) and a perfectly conducting plane at z = 2. Find

a) V at (3, 2, 4)

b)  at (3, 2, 4) c) ps at (3, 2, 2). Use method of images.

Review Question

1. Write a note on method of images.