Probability and complex function: Unit I: Probability and random variables
Moments - moment generating functions and their properties
Formula, Solved Example Problems | Random variables
Let X be discrete R.V. taking the values x1, x2,....,xn with probability mass function P1, P2, ... Pn respectively then the rth moment about the origin is
MOMENTS -
MOMENT GENERATING FUNCTIONS AND THEIR PROPERTIES :
Moments [Discrete case]
Let
X be discrete R.V. taking the values x1, x2,....,xn
with probability mass function P1, P2, ... Pn
respectively then the rth moment about the origin is

Moments [Continuous case]
If
X is a continuous R.V. with probability density function f(x) defined in the
interval (a, b) then

Moments Generating Function:
(M.G.F)
An
important device that can be used to calculate the higher moments is the moment
generating function.
Moment
generating function of a random variable X about the origin is defined as
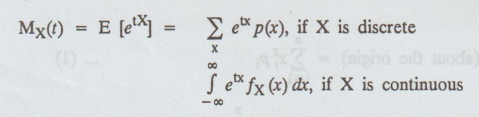
where
t being a real parameter assuming that the integration or summation is
absolutely convergent for some positive number h such that |t| < h
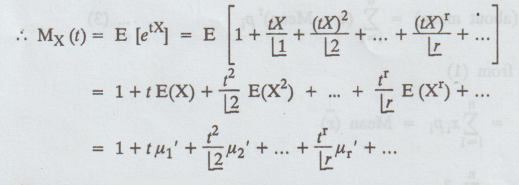
where μr' = rth moment about the origin.
E(Xf)
= ∫ xr f(x) dx or
=
∑xrp(x) depending upon X is continuous or discrete
The
coefficient of 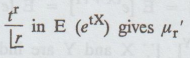
MX(t)
generates moments about the origin and hence we call it as moment generating
function.
Note1:
µr' = dr/dtr [ MX(t)]t=0
2:
MX(t) = E[et(X-a)]
(about X = a)
Where
µr' = E [ (X- a)r],
rth moment about the point X = a
Note
3 : Mean =
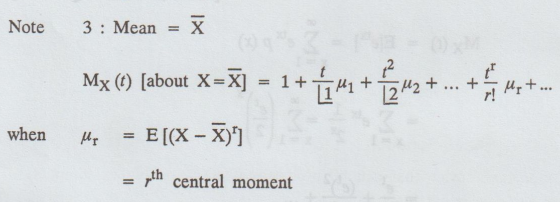
=
rth central moment
Limitations of m.g.f
1.
A random variable X may have no moment although its m.g.f exists.
2.
A random variable X can have its moment generating function and some (or all)
moments, yet the moment generating function does not generate the moments.
3.
A random variable X can have all or some moments, but moment generating
function do not exist except perhaps at one point.
Properties of moment Generating
function [A.U Tvli. A/M 2009]
1.
Let Y = aX + b, where X is a R.V with moment generating function MX
(t). Then
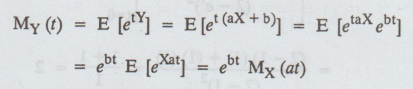
2.
McX(t) = E [ecXt] = E [eX(ct)] = MX(ct)
where c is a constant.
3.
If X and Y are two independent random variables, then
MX
+ Y (t) = MX (t). MY (t)
Proof :
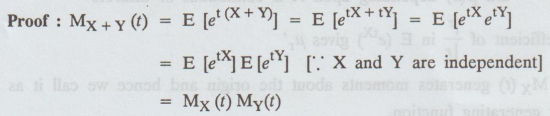
Example 1.6.1
Find the moment generating function
of the RV X whose probability function
P(X = x) 1/2x , x =
1,2,... ... Hence find its mean. [A.U Tvli A/M 2009] [A.U CBT A/M 2011] [A.U
N/D 2018 PQT R-13]
Solution
:
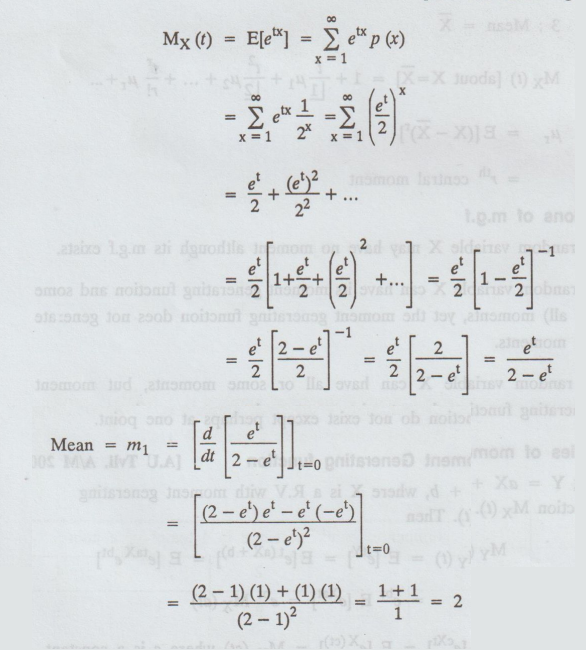
Example 1.6.2
If X represents the outcome, when a
fair die is tossed, find the moment generating function (MGF) of X and hence
find E(X) and Var(X). [A.U A/M 2018 R-13]
Solution:
The
probability distribution of X is given by
Pi
= P (X = i) = 1/6, i = 1, 2, ... 6
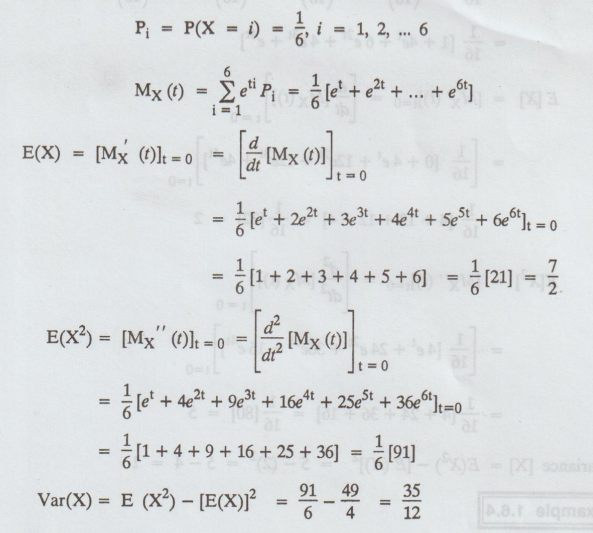
=
1/6 [ 1 + 4 + 9 + 16 + 25 + 36 ] = 1/6 [91]
Var(X)
= E (X2) - [E(X)]2 = 91/6 – 49/4 = 35/12
Example 1.6.3
Find the probability distribution
of the total number of heads obtained in four tosses of a balanced coin. Hence
obtain the MGF of X, mean of X and of a variance of X. [AU A/M 2008]
Solution :

Example 1.6.4
For a discrete random variable. X
with probability function
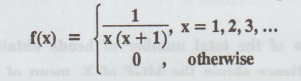
Show that E(X) does not exist
eventhough m.g.f exists. [A.U N/D 2012]
Solution:
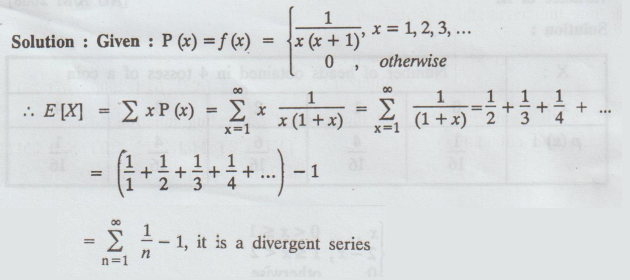
Hence,
E(X) does not exist.
Now,
we have, by definition the m.g.f as

by
using L'Hospital rule for indetermine form (0 × ∞) and MX(t) does not
exist for t > 0
Example 1.6.5
For the triangular distribution
f(x) = 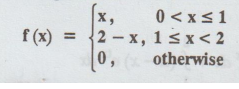 [A.U. M/J 2006, N/D 2013]
[A.U. M/J 2006, N/D 2013]
find the mean, variance and the
moment generating function (MGF) also find cdf of F(x). [A.U CBT M/J 2010, CBT
N/D 2011) [A.U N/D 2013] [A.U A/M 2018 R-08] [A.U N/D 2018 R13 RP]
Solution :
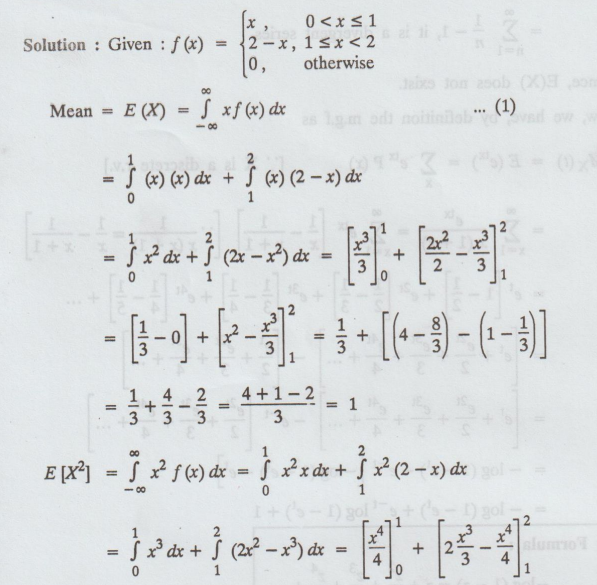
=(1/4
- 0) + (16/3 – 16/4 ) – (2/3 – 1/4 ) = 1/4 + 16/3 – 16/4 – 2/3 + 1/4
=
- 14/4 + 14/3 = -42 + 56 /12 = 14/12 = 7/6
(2)
Var (X) = E [X2] - [E (X)]2
= 7/6
– (1)2 = 7/6 – 1 = 1/6
The moment generating function of the Random variable X is
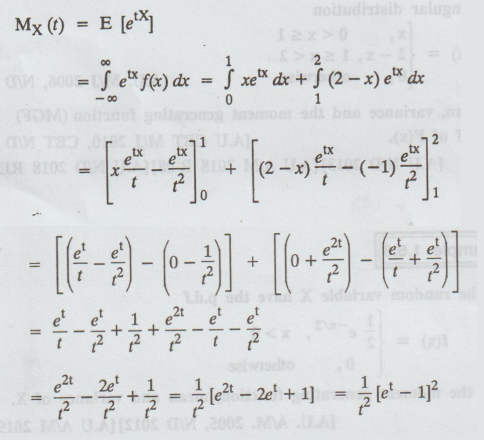
To find the cdf of F (x)
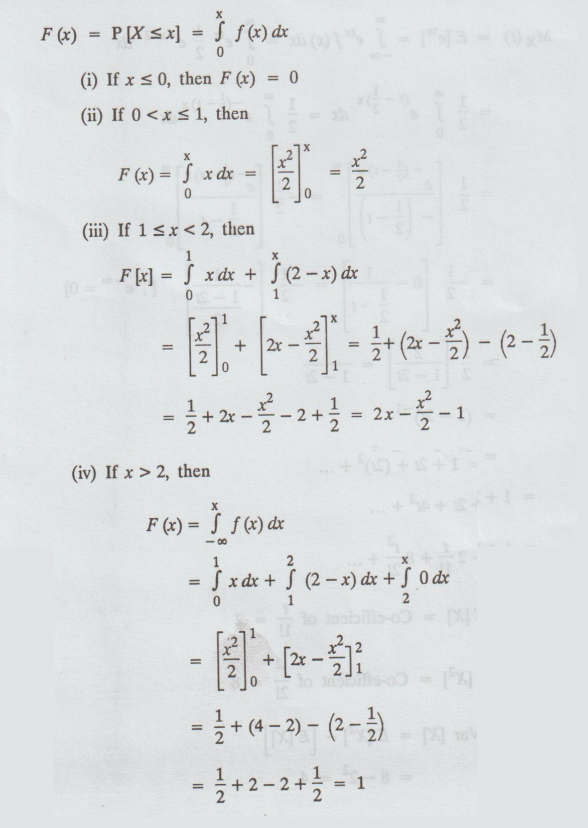
Example 1.6.6
Let the random variable X have the
p.d.f
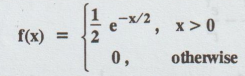
Find the moment generating
function, mean and variance of X.
[A.U. A/M. 2005, N/D 2012] [A.U A/M
2019 (R8) RP]
Solution:
The m.g.f is given by
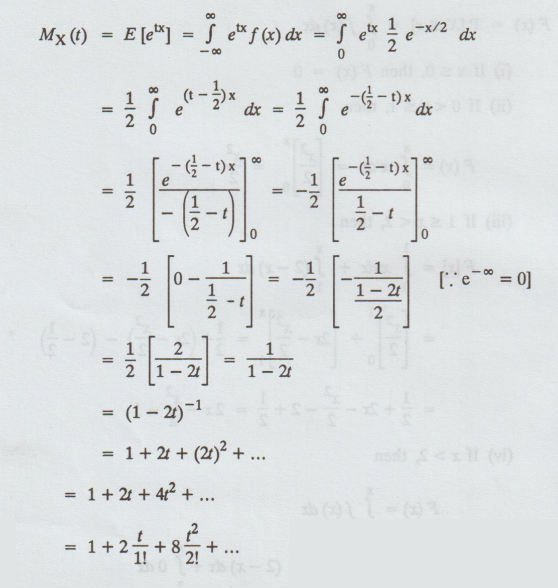
Mean
= E [X] =Co-efficient of = t /1! = 2
E[X2]
= Co-efficient of t2/2! = 8
Var
[X] = E [X2] - [E [X]]2
=
8-22 = 4
Example 1.6.7
The density function of a random
variable x is given by f(x) = Kx (2 - x), 0 ≤ x ≤ 2. Find K, mean, variance and
rth moment. [A.U. N/D 2006] [A.U. M/J 2007] [A.U Trichy A/M 2010]
Given:
f(x) = Kx (2 - x), 0 ≤ x ≤2 is a p.d.f.
We
know that, if f (x) is a p.d.f then,
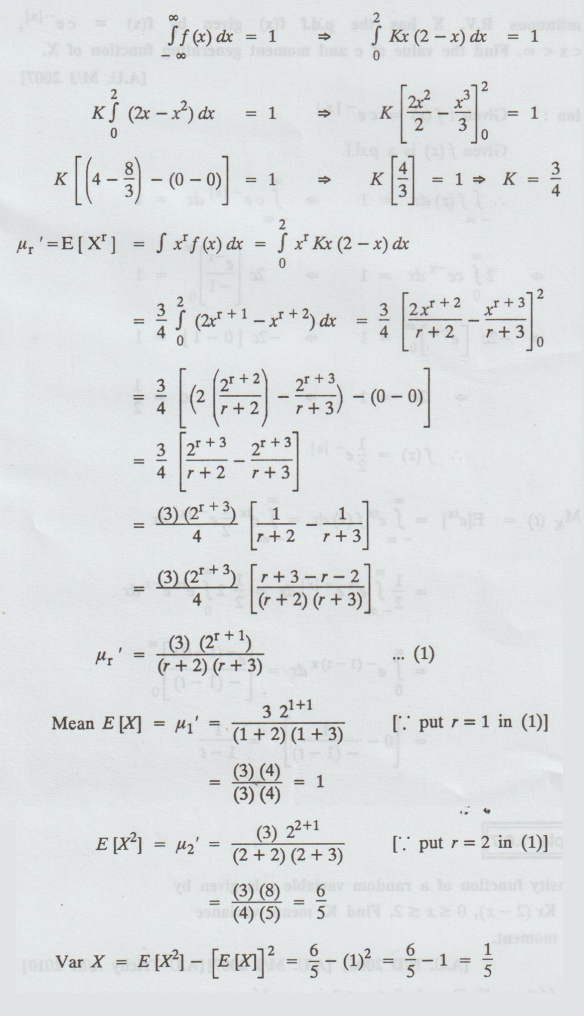
Var
X = E(X2]-[E[X]]2 = 6/5 – (1)2 = 6/5 – 1 = 1/5
Example 1.6.8
A continuous R.V. X has the p.d.f
f(x) given by f(x) = ce ̄-:x: -∞ < x < ∞. Find the value of c
and moment generating function of X. [A.U. M/J 2007]
Solution :
Given:
f(x) = ce-:x:
Given
f(x) is a p.d.f.
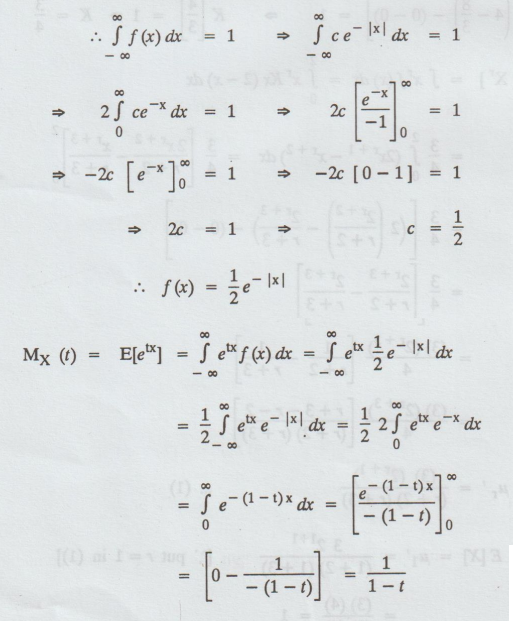
Example 1.6.9
If a R.V X has the mgf My (t) = 3 /3
– ť obtain the standard deviation of X. [A.U
A/M 2018 R-08]
Solution :
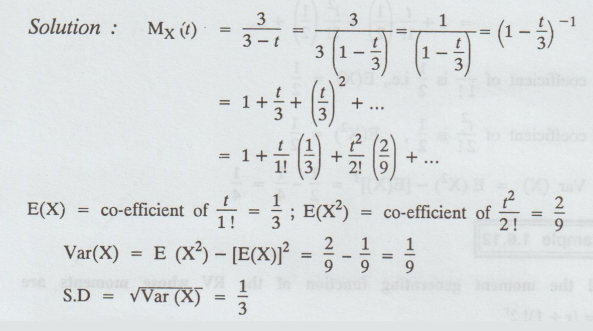
Example 1.6.10
The first four moments of a
distribution about X = 4 are 1, 4, 10 and 45 respectively. Show that the mean
is 5, variance is 3, µ3 = 0 and μ4 = 26. [A.U. N/D. 2004]
Solution :
Given that μ1'=1; μ2'=4; μ3' = 10 and μ4'
= 45.
The
point A = 4 + μ1' = 4 + 1 = 5
Variance
= μ2 = μ2' - μ1'2 = 4 - 1 = 3
μ3
= μ3' - 3 μ2'
μ1' + 2 μ1'3
=
10 - 3 (4) (1) + 2(1)3 = 10 -
12 + 2 = 0
μ4
= μ4' - 4μ3' μ1'+ 6 μ2' μ1'2
- 3 μ1'4
=
45- 4 (10) (1) +6 (4) (1)2 - 3 (1)4
=
45 - 40 + 24 – 3 = 26
Example 1.6.11
If a RV X has the moment generating
function MX (t) = 2/2 - t determine the
variance of X. [A.U M/J 2012]
Solution:
Given:
MX (t) = 2/2 - t = 2/ 2(1- t/2) = ( 1 – t/2)-1
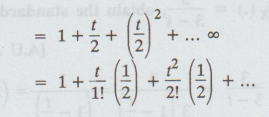
The
coefficient of 1/1! is 1/2 i.e. E(X) = 1/2
The
coefficient of of t2/2! is 1/2. E(X2) = 1/2
Var
(X) = E (X2) - [E(X)]2 = 1/2 -1/4 = 1/4
Example 1.6.12
Find the moment generating function
of the RV whose moments are mr = (r+ 1)! 2r
Solution
: The moment generating function is given by
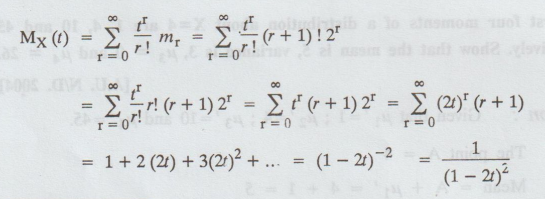
=
1 + 2 (2t) + 3 (2t)2 + ....=(1- 2t)-2 = 1/(1-2t)2
Example 1.6.13
A random variable X has density
function given by
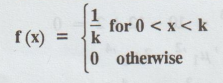
Find
(1) m.g.f. (2) rth
moment (3) mean (4) variance [AU N/D
2006]
Solution:

Variance
= E (X2) - [E(X)]2
=
k2/3- k2/4 = k2/12
Example 1.6.14
If the moments of a random variable
'X' are defined by E (Xr) = 0.6; r = 1, 2, 3, ... Show that P (X =
0) = 0.4, P (X = 1) = 0.6, P (X ≥2) = 0 [AU N/D 2008]
Solution: We
know that,
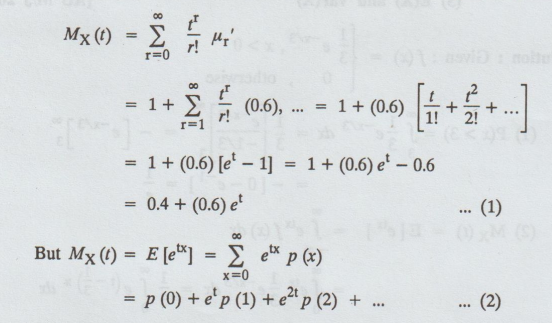
Compare
(1) & (2), we get
p
(0) = p[X = 0] = 0.4
P
(1) = p[X= 1] = 0.6
P[X
≥ 2] = 0
Example 1.6.15
Prove that the moment generating
function of the sum of a number of independent random variables is equal to the
product of their respective moment generating functions. [AU N/D 2006]
Solution:
Given:
If
X1, X2, ... Xn are n independent R.V's then
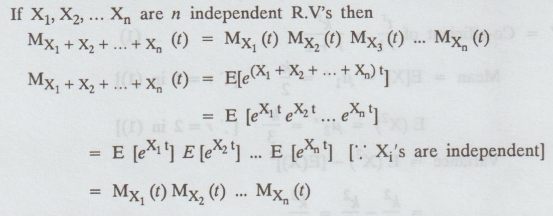
Example 1.6.16
Let
X be a R.V. with p.d.f 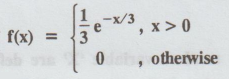
Find,
(1) P(X > 3)
(2) Moment generating function of X
(3) E(X) and Var(X)
Solution:
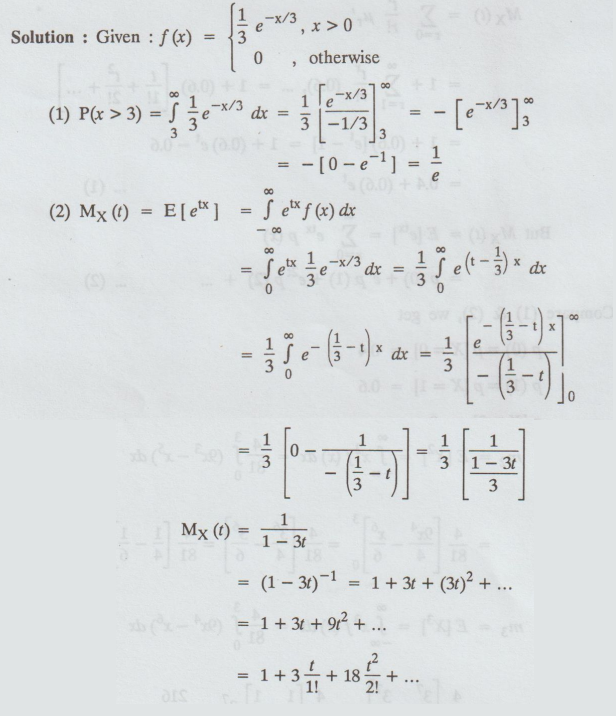
Mean
= E [X] =Co-efficient of = t /1! = 3
E[X2]
= Co-efficient of t2/2! = 18
Var
[X] = E [X2] - [E [X]]2
=
18 – [3]2 = 18 - 9 = 9
Example 1.6.17
Find the first four moments about
the origin for a random variable X having
the pdf. 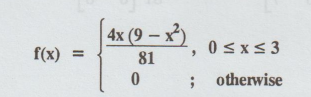
[AU N/D 2008] [A.U N/D 2016 R13
PQT] [A.U N/D 2019 (R17) PS]
Solution:
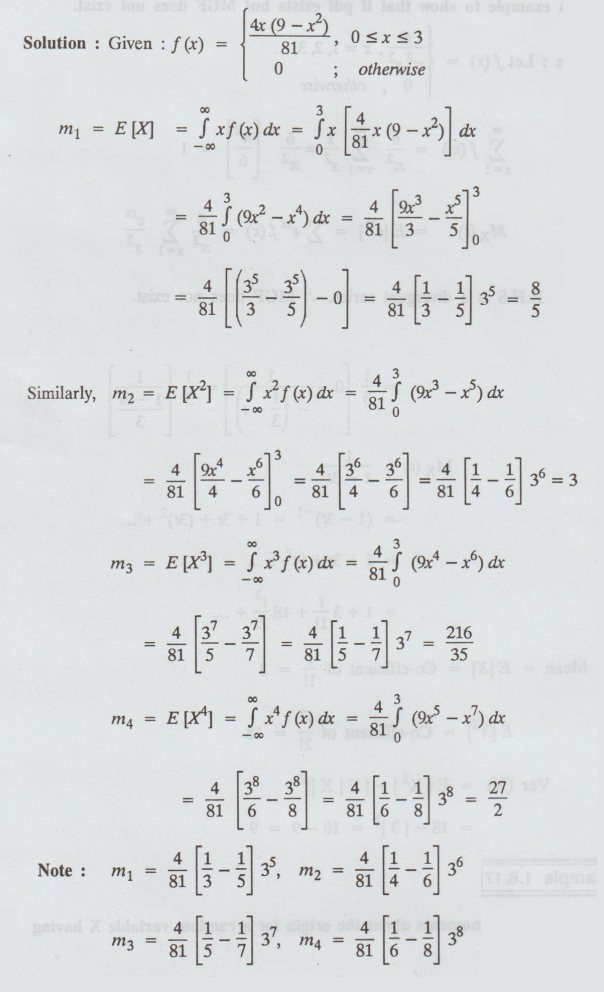
Note : m1
= 4/81 [ 1/3 – 1/5 ]35 , m2 = 4/81 [1/4- 1/6 ]36
M3
= 4/81 [1/5 – 1/7]37 , m4 = 4/81 [1/6 – 1/8 ]38
Example 1.6.18
Give an example to show that if pdf
exists but MGF does not exist.
Solution:

R.H.S
is a divergent series MGF does not
exist.
Probability
and Random Variables
Example 1.6.19
Find the M.G.F. of the random
variable X having the probability density function
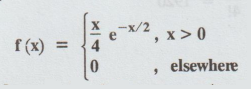
Also deduce the first four moments
about the origin. [A.U N/D 2010, M/J 2012] [A.U A/M 2017 R13]
Solution:
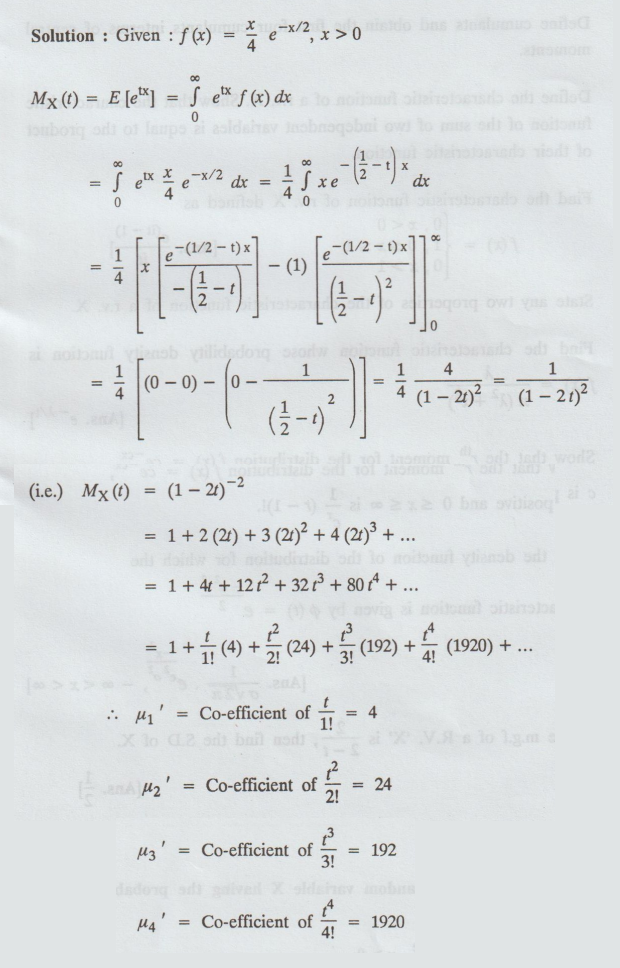
Probability and complex function: Unit I: Probability and random variables : Tag: : Formula, Solved Example Problems | Random variables - Moments - moment generating functions and their properties
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
