Monolithic Phase Locked Loop IC 565

Monolithic Phase Locked Loop IC 565

Monolithic PLLs are introduced by signetics as SE/NE 560 series and by National semiconductor as LM 560 series. The SE/NE 560 series includes SE/NE 560, 561, 562, 564, 565 and 567. These ICs are differ mainly in operating frequency range, power supply requirements, and frequency and bandwidth adjustment ranges. IC 565 PLL is most commonly used and hence discussed in this section.

1. IC 565

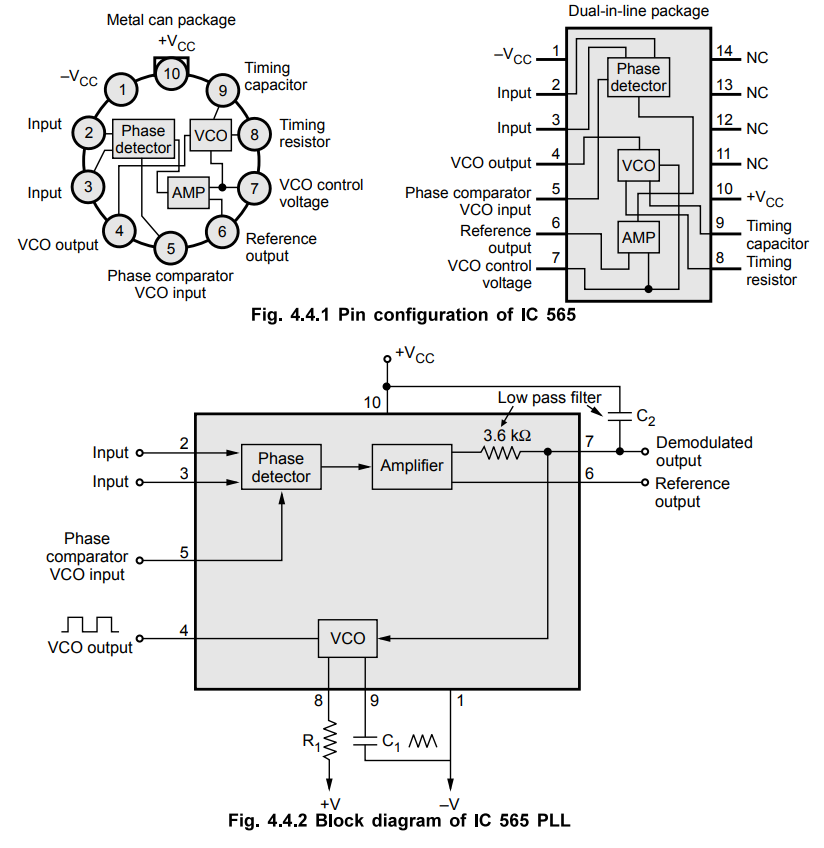
IC 565 is available in a 14 pin DIP package and 10 pin metal can package. Fig. 4.4.1 shows 14-pin package configuration for IC 565 and Fig. 4.4.2 shows the block diagram for IC 565.

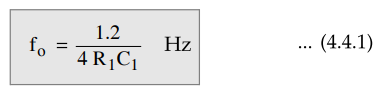
The block diagram of IC 565 PLL consists of phase detector, amplifier, low pass filter and VCO. As shown in the block diagram the phase locked feedback loop is not internally connected. Therefore, it is necessary to connect output of VCO (pin 4) to the phase comparator input (pin 5), externally. In frequency multiplication applications a digital frequency divider is inserted into the loop i.e. between pin 4 and pin 5.

The centre frequency of the PLL is determined by the free-running frequency of the VCO and it is given as

where R₁ and C₁ are an external resistor and a capacitor connected to pins 8 and 9, respectively. The values of R₁ and C₁ are adjusted such that the free running frequency will be at the centre of the input frequency range. The value of R₁ is restricted from 2 kΩ to 20 kΩ, but a capacitor can have any value. A capacitor C₂ connected between pin 7 and the positive supply (pin 10) forms a first order low pass filter with an internal resistance of 3.6 kΩ. The value of filter capacitor C₂ should be large enough to eliminate possible oscillations in the VCO voltage.

The lock range and capture range for IC 565 PLL are given by the following equations:

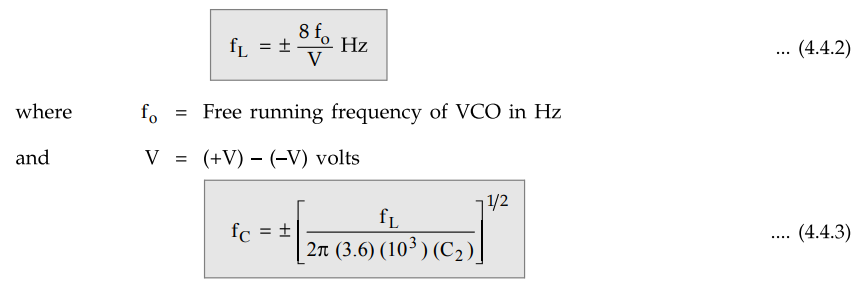
where C₂ is in farads

From equation 4.4.2 we can notice that lock range increases with an increase in input voltage but decreases with increase in supply voltage. The two inputs (pin 2 and pin 3) to the phase detector allows direct coupling of an input signal, provided that there is no dc voltage difference between the pins and the dc resistances seen from pins 2 and 3 are equal. A reference voltage at pin 6 is approximately equal to the dc voltage of the demodulated output at pin 7. This reference voltage may be used as comparator input in applications like frequency shift keying will be discussed in section 4.5. 

Example 4.4.1 For the circuit shown in the Fig. 4.4.3, calculate free running frequency, lock range and capture range.

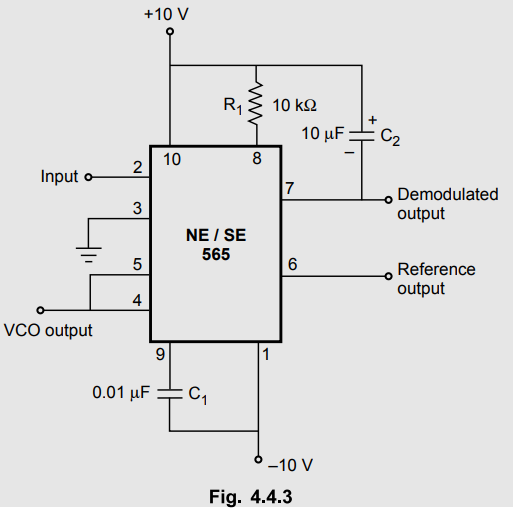
Solution :

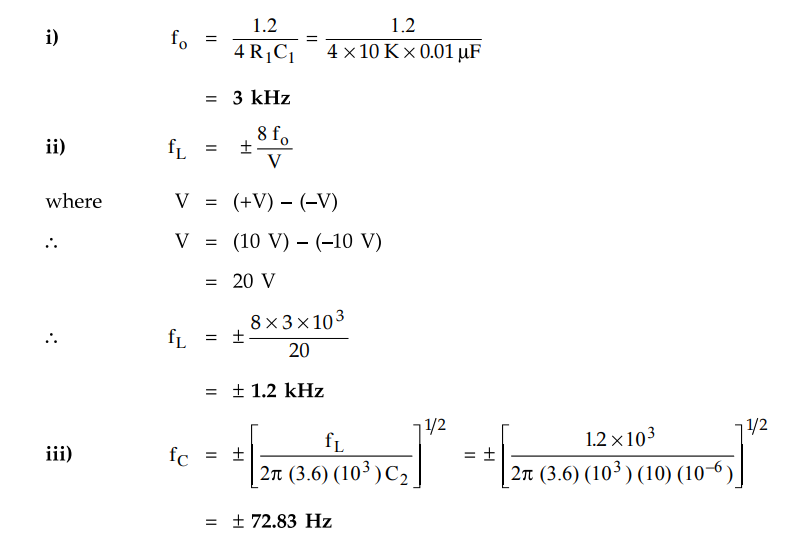
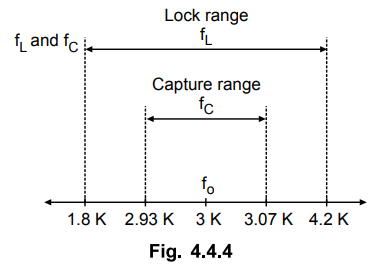
Fig. 4.4.4 shows the relationship between f_o, f_L and f_C.

Example 4.4.2 For circuit shown in Fig. 4.4.3, calculate the change in lock and capture range

if supply voltages are changed as follows :

V= 12 V and -V = -12 V

Solution : We know that, f_o = 3 kHz (calculated in the previous problem)

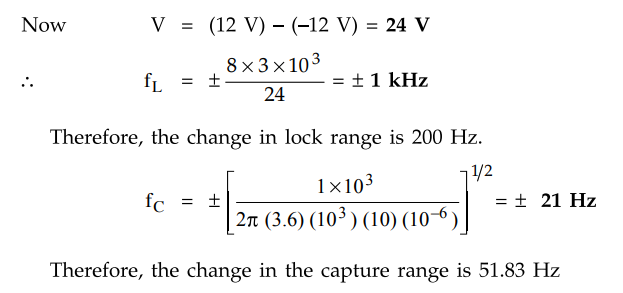
2. Derivation of LOCK Range

The Fig. 4.4.5 shows the block diagram to determine lock-range.

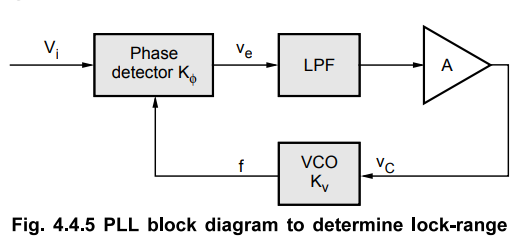
Looking at Fig. 4.4.5, let us assume that the output voltage of the phase detector is

V_e = K ϕ (θ_e - π / 2)         where θ_e = Phase error   ... (4.4.4)

The output voltage of the phase detector is filtered by the low-pass filter to remove the high frequency components. The output of the filter is amplified by a gain A and then applied as the control voltage V_C to the VCO as given by, 

v_C = Av_e = Kϕ A(θ_e  - π /2)      ...(4.4.5)

This control voltage v_C will result in a shift in the VCO frequency from its center frequency f0 to a frequency f, given by

f = f_o + K_v v_C

When the PLL is locked into the input signal frequency fi? we have

f = f_i = f_o + K_v v_C ...(4.4.6)

Substituting value v c from equation (4.4.5) we have,

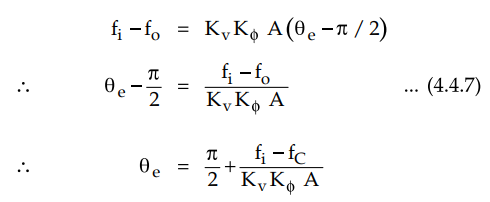
The maximum output voltage magnitude available from the phase detector occurs for ϕ = π and 0 radian and is

v_e(max) = ± Kϕ (π /2)

The corresponding value of the maximum control voltage available to drive the VCO will be

v_C(max) = ± K_ϕ (π /2) A  ...(4.4.8)

Substituting the maximum value of v C from equation (4.4.8) in equation (4.4.6) we have,

f = f_i = f_o ± K_vK_ϕ (π /2)A

f_o ± Δf_L

where 2 Δf_L will be lock-in frequency range given by,

Lock range = 2 Δf_L = K_vK_ϕ A π  Δf_L = K_vK_ϕ A π/2

The lock-in range is symmetrically located with respect to VCO free running frequency f_o. For PLL 565,

we have

3. Derivation of Capture Range

The capture range is the range of input frequencies for which the initially unlocked loop will lock on an input signal. Thus is always less than the lock range. Since capture range, Δ ω_cap denotes a transient condition, it is not as readily derived as a lock-in range. However, an approximate parametric expression for the capture range will be initially derived to give an estimate of the capture range. It can be derived by employing simple lag filter. When PLL is not locked the phase angle difference between the signal and the VCO output voltage is given by

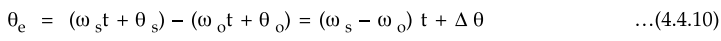
The phase angle difference thus not be constant, but will change with time at a rate given by

dθ_e / dt = ω_s - ω_o (4.4.11)

The phase detector output voltage will therefore not have a dc component, but rather will have an ac voltage with a triangular waveform of peak amplitude K (л/2) and the fundamental frequency of ω_s - ω_o i.e. f_s - f_o = Δf.

Let us derive an approximate expression for capture range for PLL employing a simple lag filter. The transfer function for a simple lag filter is given by,

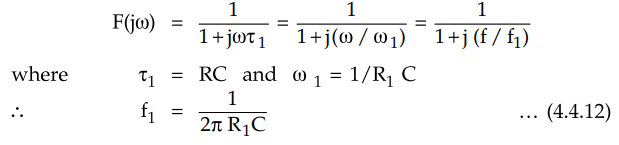
For the condition that (f/f₁)² >> 1, the transfer function can be expressed approximately as

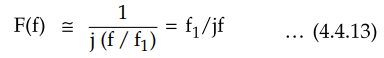
The fundamental input frequency term supplied to the low pass filter by the phase detector will be at the difference frequency Δf = f_s - f_o. If Δf  > 3f₁ the transfer function of LPF will be approximately given by,

F(Δf) = f₁ / Δf = f₁ /( f_s - f_o)       ...(4.4.14)

The voltage available to drive the VCO is given by,

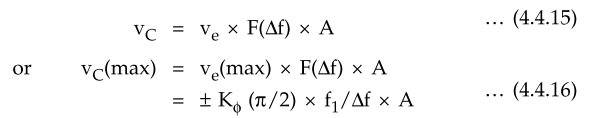
The corresponding value of the maximum frequency shift will be given by,

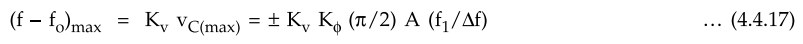
For the acquisition of the signal frequency fs, we must have that f = fs so that the maximum signal frequency range can be required by the PLL will be,

The total capture range is 2 A f_cap.

Review Questions

1. Show that the lock-in range of a PLL is given by AfL = ~ V ° w^iere symbols used have the usual meaning.

Dec.-03, 11, Marks 8

2. Derive the expression for capture range for PLL where a simple RC network is used as a low pass filter.

Dec.-l0, Marks 8

3. Briefly explain the functional block diagram of PLL IC 565.

Dec.-08,09, May-17, Marks 16