Electric Circuit Analysis: Unit V: Resonance and coupled circuits
Multiple Resonance
Resonance circuits
Circuits which exhibit more than one resonant frequency are called multiple resonant circuits.
MULTIPLE RESONANCE
Circuits
which exhibit more than one resonant frequency are called multiple resonant
circuits.
L1
C1 series resonant at f1. Inductive at f2.
F2
> f1
L1
C1 in parallel with C2 is parallel resonant at ƒ2.
ω1
= 2π f1; ω2 = 2π f2; 0 = 2π f
Where
ƒ is any frequency.
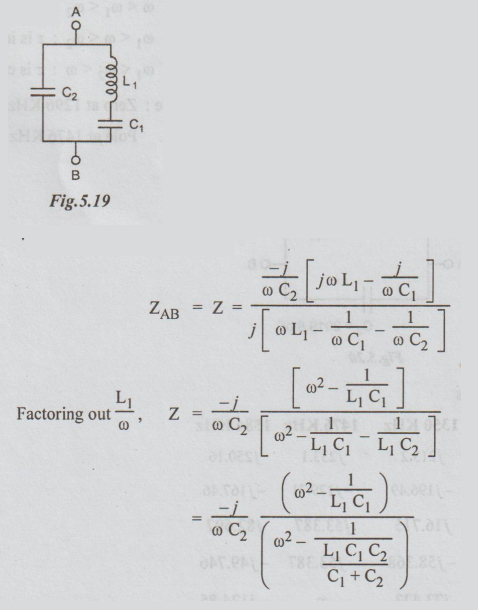
At
ω2, Reactance of L1 C1 arm = Reactance of C2
arm
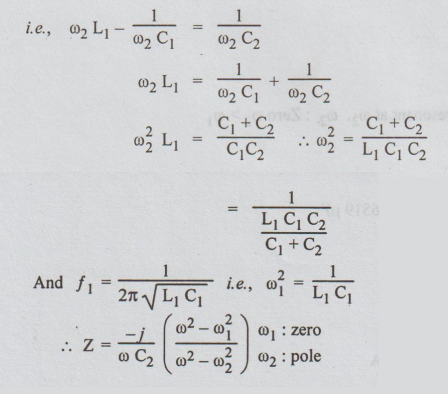
Here,
pole is greater than zero.
ω1
< ω1 : ω2 : z is capacitive
ω1
< ω < ω2 : z is inductive
ω1
< ω2 < ω : z is capacitive
Example:
Zero at 1296 KHz
Pole
at 1476 KHz
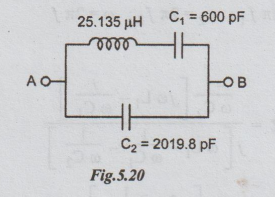
Capacitive
at all other frequencies
Reactance
of: 936 KHz 1296 KHz 1350 KHz
L1
|| C1 is capacitive for ω > ω1
L0
in series with L1 || C1 is series resonant at ω2
ω2 : Zero ω2 > ω1
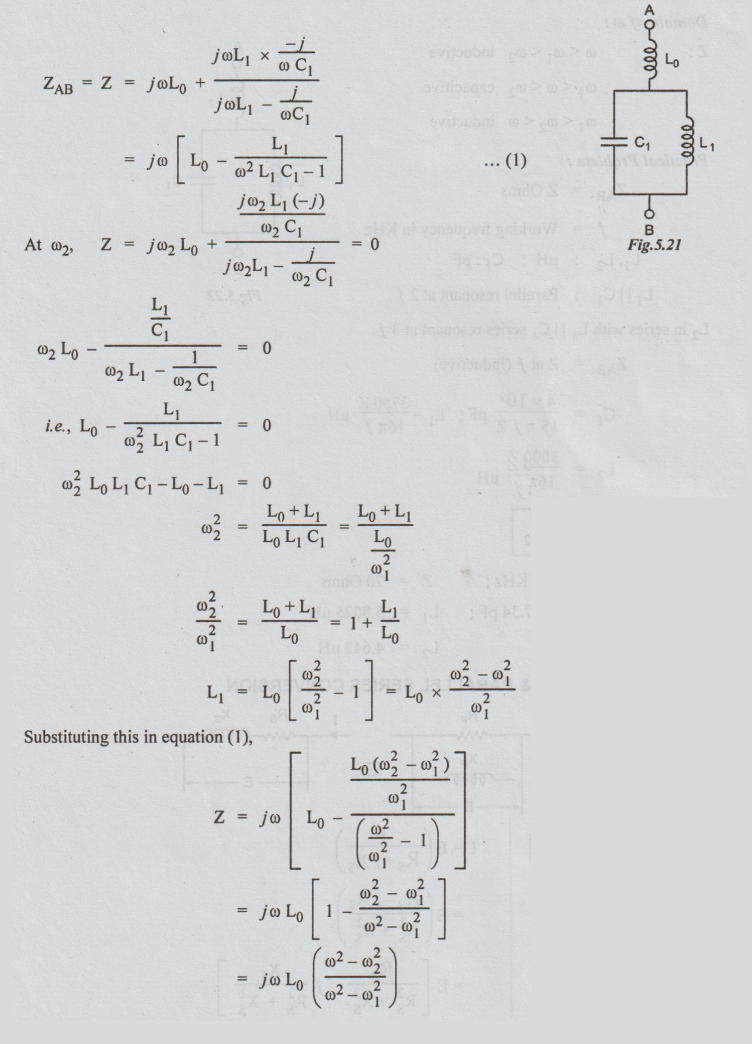
Domain
of ω :
Z:
ω < ω2 inductive
ω1
< ω < ω2 capacitive
ω1
< ω2 < ω inductive
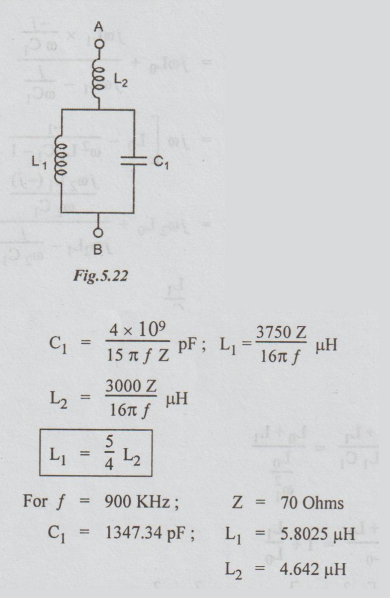
Practical
Problem:
ZAB
= Z Ohms
f
= Working frequency in KHz
L1,
L2 : μH ; C1: pF
L1
|| C1 : Parallel resonant at 2 f
L2
in series with L1 || C1 series resonant at 3 f.
ZAB
= Z at f (inductive)
Electric Circuit Analysis: Unit V: Resonance and coupled circuits : Tag: : Resonance circuits - Multiple Resonance
Electric Circuit Analysis: Unit V: Resonance and coupled circuits
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation