Mutually Induced E.M.F. and Mutual Inductance

Mutually Induced E.M.F. and Mutual Inductance

AU: Dec.-12, May-14,17

 • If the flux produced by one coil is getting linked with another coil and due to change in this flux produced by first coil, there is induced e.m.f. in the second coil, then such an e.m.f. is called mutually induced e.m.f.

 • Consider two coils which are placed adjacent to each other as shown in the Fig. 1.24.1. The coil A has N, turns while coil B has N₁, number of turns. The coil A has switch S, variable resistance R and battery of 'E' volts in series with it. A galvanometer is connected across coil B to sense induced e.m.f. and current because of it.

• Current through coil A is I₁ producing flux 01. Part of this flux will link with coil B i.e. will complete its path through coil B as shown in the Fig. 1.24.1. This is the mutual flux ϕ₂.

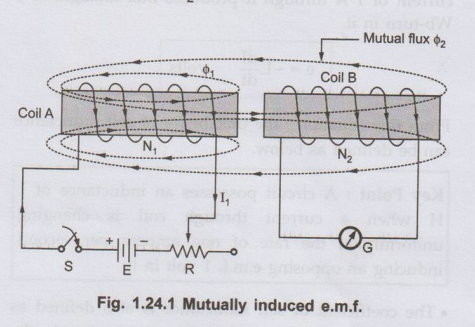
Now if current through coil A is changed by means of variable resistance R, then flux 0, changes. Due to this, flux associated with coil B, which is mutual flux 02 also changes. Due to Faraday's law there will be induced e.m.f. in coil B which will set up a current through coil B, which will be detected by galvanometer G.

Key Point : Any change in current through coil A produces e.m.f. in coil B, this phenomenon is called mutual induction and e.m.f. is called mutually induced e.m.f.

1. Magnitude of Mutually Induced E.M.F.

 Let

N₁ = Number of turns of coil A,

N₂ = Number of turns of coil B

I₁ = Current flowing through coil A

Φ₁ = Flux produced due to current I, in webers.

ϕ₂ = Flux linking with coil B

According to Faraday's law, the induced e.m.f. in coil B is,

e₂ = -N₂ dϕ₂/d₁

Negative sign indicates that this e.m.f. will set up a current which will oppose the change of flux linking with it.

Now  ϕ2 = ϕ₂/I₁ ×I₁

If permeability of the surroundings is assumed constant then ϕ2∞ I₁, and hence ϕ₂/I₁, is constant.

Coefficient of mutual inductance is defined as the property by which e.m.f. gets induced in the second coil because of change in current through first coil.

Coefficient of mutual inductance is also called mutual inductance. It is measured in henries

2. Definitions of Mutual Inductance and its Unit

1) The coefficient of mutual inductance is defined as the flux linkages of the coil per ampere current in other coil.

2) It can also be defined as equal to e.m.f. induced in volts in one coil when current in other coil changes uniformly at a rate of one ampere per second.

Similarly its unit can be defined as follows :

1. Two coils which are magnetically coupled are said to have mutual inductance of one henry when a current of one ampere flowing through one coil produces a flux linkage of one weber turn in the other coil.

2. Two coils which are magnetically coupled are said to have mutual inductance of one henry when a current changing uniformly at the rate of one ampere per second in one coil, induces as e.m.f. of one volt in the other coil.

3. Expressions of the Mutual Inductance (M)

4. Coefficient of Coupling or Magnetic Coupling Coefficient

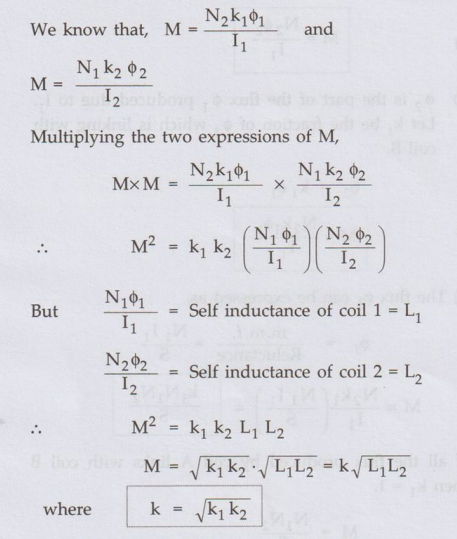
• The k is called coefficient of coupling.

• If entire flux produced by one coil links with other then k = k₁ = k₂ = 1 and maximum mutual inductance existing between the coil is M = k√L₁L₂

• This gives an idea about magnetic coupling between the two coils. When entire flux produced by one coil links with other, this coefficient is maximum i.e. Unity.  

• It can be defined as the ratio of the actual mutual inductance present between the two coils to the maximum possible value of the mutual inductance.                              

• The expression for k is,

k = M/√L₁L₂

Key Point : When k = 1 coils are said to be tightly coupled and if k is a fraction the coils are said to be loosely coupled.

Ex. 1.24.1 Two coils A and B are kept in parallel planes, such that 70 % of the flux produced by coil A links with coil B. Coil A has 10,000 turns. Coil B has 12,000 turns. A current of 4 A in coil A produces a flux of 0.04 mWb while a current of 4 A in coil B produces a flux of 0.08 mWb. Calculate,   i) Self inductances L_A, and L_B ii) Mutual inductance M iii) Coupling coefficient.

Sol. : The given values are,

Ex. 1.24.2. Two coils A and B are wound on same iron core. There are 600 turns on A and 3600 turns on B. The current of 4 amps through coil A produces a flux of 500x10^-6 Wb in the core. If this current is reversed in 0.02 second calculate average e.m.f. induced in coils A and B. AU : Dec.-12, Marks 8

Sol. :

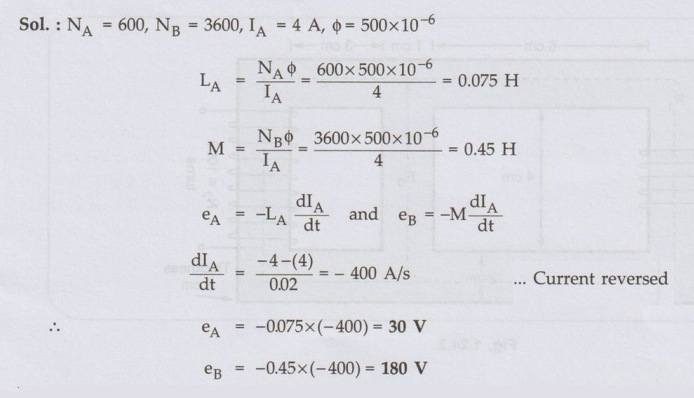
Ex. 1.24.3 Two coils A and B, have self inductances of 120 µH and 300 µH respectively. A current of 1 A through coil 'A' produces flux linkage of 100 µWb turns in coil 'B'. Calculate i) Mutual inductance between the coil.

ii) Average e.m.f. induced in coil 'B' if current of 1 A in coil 'A' is reversed at a uniform rate in 0.1 sec. Also find coefficient of coupling.

Sol. :

Ex. 1.24.4 For the magnetic circuit as shown in Fig. 1.30.2, find the self and mutual inductance between the two coils. Assume core permeability = 1600. AU : May-14, Marks 13

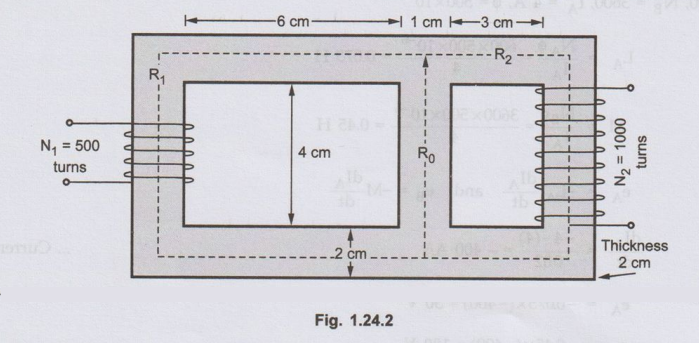
Sol. :

Review Questions

1. Derive the various expressions for the mutual inductance. AU: Dec.-12, May-17, Marks 4

2. Derive the expression for coefficient of coupling. AU : May-17, Marks 4         

3. Two identical 1000 turn coils X and Y lie in parallel planes such that 60 % of the flux produced by one coil links with the other. A current of 5 A in X produces a flux of 5x10^-6Wb in itself. If the current in X changes from + 6 A to - 6 A in 0.01 sec, what will be the magnitude of the e.m.f. induced in Y ? Calculate the self inductance of each coil.

(Ans. : 0.72 V, 0.001 H)                                                

4. Two 200 turns, air cored solenoids, 25 cm long have a cross-sectional area of 3 cm² each. The mutual inductance between them is 0.5 µH. Find the self inductance of the coils and the coefficient of coupling. 

(Ans. : 60.31 uH, 0.00828)

 5. Two coils A and B having 5000 and 2500 turns respectively are wound on a magnetic ring. 60 % of the flux produced by coil A links with coil B. A current of 1 A produces a flux of 0.25 mWb in coil A while same current produces a flux of 0.15 mWb in coil B. Find the mutual inductance and coefficient of coupling. 

(Ans. : 1.25 H, 0.375 H, 0.5477)

6. Two long, single-layered solenoids 'x' and 'y' have the same length and the same number of turns. The cross-sectional areas of the two are 'a_x' and 'a_y' respectively, with 'a_y' < 'a_x'. They are placed coaxially, with solenoid 'y' placed within the solenoid 'x'. Show that the coefficient of coupling between them is equal to √a_y/a_y.

7. A coil of 200 turns having a mean diameter of 6 cm is placed coaxially at the centre of a solenoid of 50 cm long with 1500 turns and carrying current of 2.5 A. Calculate the mutual inductance between the two coils.

(Ans. : 2.1318 mH)            

8. Two coils A and B are placed such that 40 % of flux produced by coil A links with coil B coils A and B have 2000 and 1000 turns respectively. A current of 2.5 A in coil A produces a flux of 0.035 mWb in coil B. For the above coil combination, find out i) M, the mutual inductance and ii) the coefficient of coupling k_A, k_B and k iii) Self inductances L_A and L_g. 

[Ans. : 0.014 H, 0.07 H, 0.014 H, 0.5, 0.4, 0.4472]