Nature of the Induced E.M.F.

Nature of the Induced E.M.F.

AU : May-12, Dec.-13,14,15,16,19

• E.M.F. gets induced in a conductor, whenever there exists change in flux with that conductor, according to Faraday's Law. Such change in flux can be brought about by different methods.

• Depending upon the nature of methods, the induced e.m.f. is classified as,      

1) Dynamically induced e.m.f. and

2) Statically induced e.m.f

1. Dynamically Induced E.M.F.

• The change in the flux linking with a coil, conductor or circuit can be brought about by its motion relative to magnetic field. This is possible by moving flux with respect to coil conductor or circuit or it is possible by moving conductor, coil, circuit with respect to stationary magnetic flux. Both these methods are discussed earlier in discussion of Faraday's experiment

Key Point : Such an induced e.m.f. which is due to physical movement of coil, conductor with respect to flux or movement of magnet with respect to stationary coil, conductor is called dynamically induced e.m.f. or motional induced e.m.f.

a. Magnitude of Dynamically Induced E.M.F.

 • Consider a conductor of length 1 metres moving in the air gap between the poles of the magnet.

If plane of the motion of the conductor is parallel to the plane of the magnetic field then there is no cutting of flux lines and there can not be any induced e.m.f. in the conductor such condition is shown in the Fig. 1.22.1 (a).

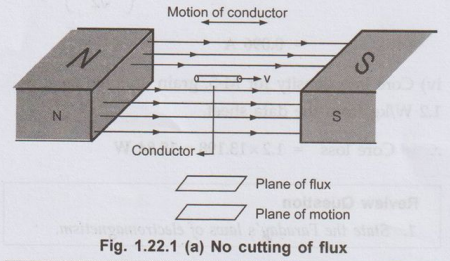
Key Point : When plane of the flux is parallel to the plane of the motion of conductors then there is no cutting of flux, hence no induced e.m.f.

•In second case as shown in the Fig. 1.22.1 (b), the velocity direction i.e. motion of conductor is perpendicular to the flux. Hence whole length of conductor is cutting the flux line hence there is maximum possible induced e.m.f. in the conductor. Under such condition plane of flux and plane of motion are perpendicular to each other.

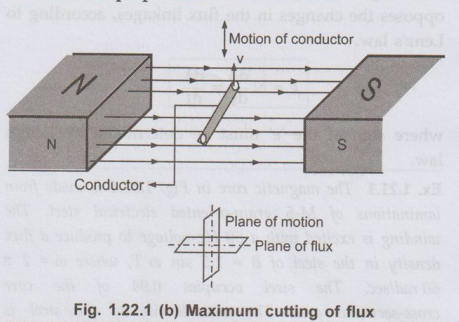
Key Point : When plane of the flux is perpendicular to the plane of the motion of the conductors then the cutting of flux is maximum and hence induced e.m.f. is also maximum.

Consider a conductor moving with velocity v m/s such that its plane of motion or direction of velocity is perpendicular to the direction of flux lines as shown in Fig. 1.22.2 (a).

B = Flux density in Wb/m²  

l = Active length of conductor in metres.

(This is the length of conductor which is actually responsible for cutting of flux lines.)

V = Velocity in m/sec.

Let this conductor is moved through distance dx in a small time interval dt, then

Area swept by conductor = 1 ×  dx m²

ஃ Flux cut by conductor = Flux density × Area swept

dϕ = B×l× dx Wb

 According to Faraday's law, magnitude of induced e.m.f. is proportional to the rate of change of flux.

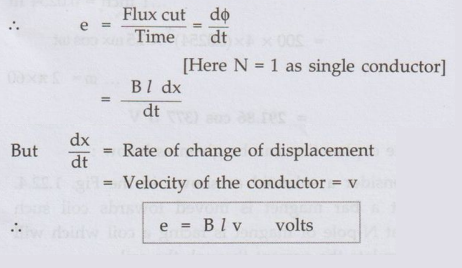
• This is the induced e.m.f. when plane of motion is exactly perpendicular to the plane of flux. This is maximum possible e.m.f. as plane of motion is at right angles to plane of the flux.

• But if conductor is moving with a velocity v but at a certain angle O measured with respect to direction of the field (plane of the flux) as shown in the Fig. 1.22.2 (b) then component of velocity which is v sin 0 is perpendicular to the direction of flux and hence responsible for the induced e.m.f. The other component v cos O is parallel to the plane of the flux and hence will not contribute to the dynamically induced e.m.f.   

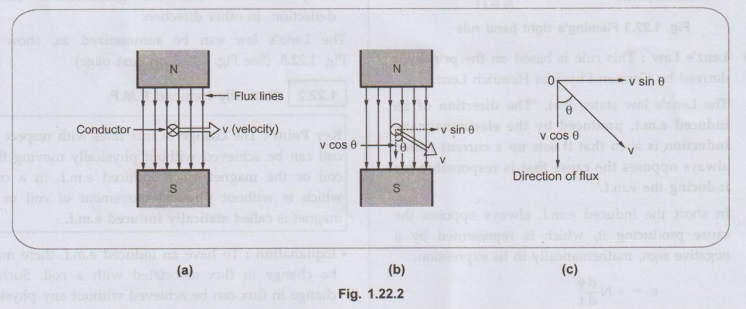
• Under this condition magnitude of induced e.m.f. is given by,

e = B l v sin θ volts

where θ  is measured with respect to plane of the flux.

Ex. 1.22.1 A conductor of 2 m length moves with a uniform velocity of 1.27 m/sec under a magnetic field having a flux density of 1.2 Wb/m² (tesla). Calculate the magnitude of induced e.m.f. if conductor moves,

i)At right angles to axis of field.

ii) At an angle of 60° to the direction of field.

Sol. : The magnitude of induced e.m.f.

Ex. 1.22.2 A coil carries 200 turns gives rise a flux of 500 μWb when carrying a certain current. If this current is reversed in 1/10 th of a second. Find the average e.m.f. induced in the coil.

Sol. The magnitude of induced e.m.f. is,

= N d ϕ / dt

where d ϕ is change in flux linkages i.e. change in N ϕ. Now in this problem flux is 500 × 10^-6 for given current. After reversing this current, flux will reverse its direction. So flux becomes (-500 × 10^-6).

. d ϕ = ϕ₂ – ϕ₁ -500× 10^-6 -(+ 500 × 10^-6)

This happens in time dt = 0.1 sec.

Average e.m.f. = N d ϕ / dt = -200× (-1 × 10³ / 0.1)

= 2 volts

Ex. 1.22.3 An electric conductor of effective length of 0.3 metre is made to move with a constant velocity of 5 metre per second perpendicular to a magnetic field of uniform flux density 0.5 tesla. Find the e.m.f. induced in it. If this e.m.f. is used to supply a current of 25 A, find the force on the conductor, and state its direction w.r.t. motion of conductor, ignoring friction. Find the power required to keep the conductor moving across the field.

Sol : 

1 = 0.3 m, v = 5 m/s, B = 0.5 T 

ஃ e = Blv = 0.3 × 5 × 0.5 = 0.75 V and I = 25 A 

ஃ F = BI l = 0.5 ×  25 × 0.3 = 3.75 N 

The direction of this force is so as to oppose the motion of conductor, as per Lenz's law. The power required to keep the conductor moving is,

P = e × I = 0.75 × 3.75 = 2.8125 W

b. Direction of Dynamically Induced E.M.F.

 The direction of induced e.m.f. can be decided by using two rules.

1) Fleming's Right Hand Rule :

 Fleming's Right Hand Rule is to used to get direction of induced e.m.f. when conductor is moving in a magnetic field.

According to Fleming's right hand rule, outstretch the three fingers of right hand namely the thumb, fore finger and the middle finger, perpendicular to each other. Arrange the right hand so that first finger point in the direction of flux lines (from N to S) and thumb in the direction of motion of conductor with respect to the flux then the middle finger will point in the direction of the induced e.m.f. (or current). The rule is shown in the Fig. 1.22.3.

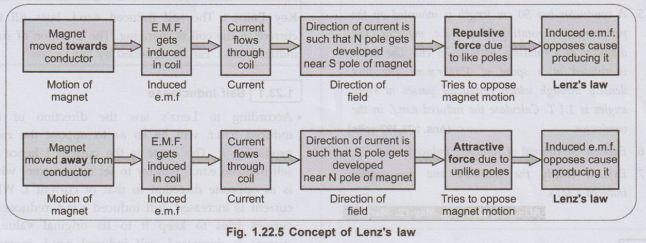
2) Lenz's Law : This rule is based on the principles derived by German Physicist Heinrich Lenz.

 The Lenz's law states that, 'The direction of an induced e.m.f. produced by the electromagnetic induction is such that it sets up a current which always opposes the cause that is responsible for inducing the e.m.f.' In short the induced e.m.f. always opposes the cause producing it, which is represented by a negative sign, mathematically in its expression.

ஃ  e = - N dϕ/dt

The explanation can be given as below : Sud Consider a solenoid as shown in the Fig. 1.22.4. Let a bar magnet is moved towards coil such that N-pole of magnet is facing a coil which will circulate the current through the coil.

• According to Lenz's Law, the direction of current due to induced e.m.f. is so as to oppose the cause. The cause is motion of bar magnet towards coil. So e.m.f. will set up a current through coil in such a way that the end of solenoid facing bar magnet will become N-pole. Hence two like poles will face each other experiencing force of repulsion which is opposite to the motion of bar magnet as shown in the Fig. 1.22.4.

• If the same bar magnet is moved away from the coil, then induced e.m.f. will set up a current in the direction which will cause, the end of solenoid facing bar magnet to behave as S-pole. Because of this two unlike poles face each other and there will be force of attraction which is direction of magnet, away from the coil. The galvanometer shows deflection in other direction.

 The Lenz's law can be summarized as, show in Fig. 1.22.5.

2. Statically Induced E.M.F.

Key Point : The change in flux lines with respect to coil can be achieved without physically moving the coil or the magnet. Such induced e.m.f. in a coil which is without physical movement of coil or a magnet is called statically induced e.m.f.

• Explanation : To have an induced e.m.f. there must be change in flux associated with a coil. Such a change in flux can be achieved without any physical movement by increasing and decreasing the current producing the flux rapidly, with time.

 • Consider an electromagnet which is producing the necessary flux for producing e.m.f. Now let current through the coil of an electromagnet be an alternating one. Such alternating current means it changes its magnitude periodically with time. This produces the flux which is also alternating i.e. changing with time. Thus there exists dϕ / dt associated with coil placed in the viscinity of an electromagnet. This is responsible for producing an e.m.f. in the coil. This is called statically induced e.m.f.

Key Point : It can be noted that there is no physical movement of magnet or conductor, it is the alternating supply which is responsible for such an induced e.m.f.

The concept of statically induced e.m.f. is shown in the Fig. 1.22.6.

Such an induced e.m.f. can be observed in case of a device known as transformer.

Key Point : Due to alternating flux linking with the coil itself, the e.m.f. gets induced in that coil itself which carries an alternating current.

The statically induced e.m.f. is further classified as,

1) Self induced e.m.f. and

2) Mutually induced e.m.f.

 Review Questions

1. Derive the expression for the magnitude of the dynamically induced e.m.f.

AU : Dec.-16, 19, Marks 8

2. Explain Fleming's right hand rule.

3. Explain Lenz's law.

4. A square coil of 20 cm side is rotated about its axis at a speed of 200 revolutions per minute in a magnetic field of density 0.8 Wblm . If the number of turns of coil is 25, determine maximum e.m.f. induced in the coil. (Ans. : 16.75 V)

5. A conductor has 50 cm length is mounted on the periphery of a rotating part of d.c. machine. The diameter of a rotating drum is 75 cm. The drum is rotated at a speed of 1500 r.p.m. The flux density through which conductor passes at right angles is 1.1 T. Calculate the induced e.m.f. in the conductor. (Ans. : 32.397 volts)

6. Explain the concept of statically induced e.m.f.

7. Explain clearly the statically and dynamically induced EMFs. AU : Dec.-13,14,15, May-12, Marks 4