Normal distributions: Solved Example Problems

Example 1.12.1

X is a normal variate with mean 30 and S.D 5. Find the probabilities that (i) 26 ≤ X ≤ 40, (ii) X ≥ 45, (iii) |X - 30❘ > 5 [A.U Tvli A/M 2009]

Solution :

Given: μ = 30, σ = 5

 

Example 1.12.2

A normal distribution has mean μ = 20 and standard deviation σ = 10. Find P(15≤ X ≤ 40)

Solution:

Given: μ = 20, σ = 10

 

Example 1.12.3

The average seasonal rainfall in a place in 16 inches with a S.D. of 4 inches. What is the probability that in a year the rainfall in that place will be between 20 and 24 inches ?

Solution:

 

Example 1.12.4

If X is a random variable normally distributed with mean zero and variance σ², find E [| X |].

Solution:

E [| X |] = Mean deviation about origin

= Mean deviation about mean (mean = 0)

Mean deviation about mean = 4/5 σ E [ | X |] = 4/5 σ.

 

Example 1.12.5

X is a normal variate with mean 1 and variance 4. Y is another normal variate independent of X with mean 2 and variance 3. What is the distribution of X + 2Y.

Solution:

Since X and Y are independent normal variates, X + 2Y will also be a normal variate by the addition property and

Mean of (X + 2Y) = E(X + 2Y) = E(X) + 2E(Y)

= 1 + 2 × 2 = 5 ['.' E(X) = 1, E(Y) = 2}

Variance of (X + 2Y) = V(X + 2Y) = V(X) + 4V(Y)

[ X and Y are independent]

= 4 + 4 × 3 = 16 ['. V(X) = 4, V(Y) = 3]

X + 2Y will follow normal with mean 5 and variance 16.

 

Example 1.12.6

If X is normal with mean 2 and standard deviation 3, describe the distribution

of Y = 1/2 X - 1 find P[Y ≥ 3/2]

Solution:

Given X follows normal with mean 2 and variance 9.

The distribution of Y = ɑx + b is also normal with

 

Example 1.12.7

In a normal distribution, 31% of the items are under 45 and 8% are over 64. Find the mean and variance of the distribution.

[A.U N/D 2015 R13, RP] [A.U A/M 2019 (R13) RP]

Solution :

We know that, Z = X - µ / σ

 

Example 1.12.8

(i) A company finds that the time taken by one of its engineers to complete or repair job has a normal distribution with mean 40 minutes and standard deviation 5 minutes. State what proportion of jobs take: (a) less than 35 minutes (b) more than 48 minutes

(ii) The company charges Rs. 20 if the job takes less than 35 minutes, Rs. 40 if it takes between 35 and 48 minutes and Rs. 70 if it takes more than 48 minutes. Find the average charge for a repair job.

Solution:

(i) (a) We know that, Z = X - μ / σ = X – 40 / 5

When

X = 35

Z = 35 - 40 / 5 = 1

= 0.5 - P [0 ≤  Z ≤ 1]

= 0.5 - 0.3413

= 0.1587

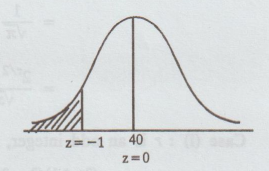
Proportion of jobs which takes less than 35 minutes = 0.1587

 

Example 1.12.9

Find the nth central moments of normal distribution.

[AU M/J 2007] [A.U N/D 2014 (RP) R-8]

Solution : Central moments of the normal distribution N(µ, σ)

Central moments µ_r of N(µ, σ) are given by μ_r

(3) gives a recurrence relation for the even order central moments of the normal distribution N (µ, σ).

Example 1.12.10

The savings bank account of a customer showed an average balance of Rs. 150 and a standard deviation of Rs. 50. Assuming that the account balances are normally distributed.

1. What percentage of account is over Rs. 200 ?

2. What percentage of account is between Rs. 120 and Rs. 170 ?

3. What percentage of account is less than Rs. 75 ?

[AU N/D 2006]

Solution: Given: μ = 150, σ = 50

 

Example 1.12.11

An electrical firm manufactures light bulbs that have a life, before burn-out, that is normally distributed with mean equal to 800 hours and a standard deviation of 40 hours. Find [AU N/D 2006]

(1) the probability that a bulb burns more than 834 hours JedW

(2) the probability that bulb burns between 778 and 834 hours.

[A.U N/D 2018 R-13 PQT]

Solution : (1) Given: μ = 800 hours

 σ = 40 hours

 

Example 1.12.12

The mean yield for one-acre plot is 662 kilos with standard deviation 32 kilos. Assuming normal distribution, how many one-acre plots in a patch of 1,000 plots would you expect to have yield over 700 kilos, below 650 kilos. [AU A/M 2008]

Solution: Given: μ = 662, σ = 32

Standard normal variate

Z = X – μ / σ =  X - 662 / 32

 

Example 1.12.13

In a distribution exactly normal 7% of the items are under 35 and 89% are under 63. What are the mean and standard deviation of the distribution ?

[AU Nov. 2005]

Solution:

We know that, Z = X - µ / σ

 

Example 1.12.14

The independent RVS X and Y have distributions N(45, 2) and N(44, 1.5) respectively. What is the probability that randomly chosen values of X and Y differ by 1.5 or more? [A.U N/D 2011]

Solution : X is N (45, 2) and Y is N(44, 1.5)

By the property of additive

U = X - Y follows the distribution N (1, √4 + 2.25)

i.e., N (1, 2.5)

P[X and Y differ by 1.5 or more]

 

Example 1.12.15

If X and Y are independent RVs, each following N(0, 3), what is the probability that the point (X, Y) lies between the lines 3X+ 4Y = 5 and 3X+4Y = 10? Solution X follows N(0, 3) and Y follows N (0, 3).

U = 3X + 4Y follows N [3 × 0 + 4 × 0, √9 × 9 +16 × 9]

i.e., N(0, 15)

P[the point (X, Y) lies between the lines

3X + 4Y = 5 and 3X + 4Y = 10]}

= P [5 < 3X + 4Y < 10]

= P [5 < U < 10]

 

Example 1.12.16

The peak temperature T, as measured in degrees Fahrenheit, on a particular day is the Gaussian (85, 10) random variable. What is P (T > 100). P (T60) and P [70 ≤ T ≤ 100] ? [A.U A/M. 2015, R13]

Solution:

Given: μ = 85, σ = 10