Norton's Theorem

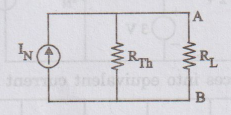
NORTON'S THEOREM

Statement

Any two terminal network containing linear, passive and active elements may be replaced by an equivalent current source I_N in parallel with a resistance RN where IN is the current flowing through a short circuit placed across the terminals AB and RN is the equivalent resistance of the network as seen from the two terminals with all independent sources are replaced by their internal resistances.

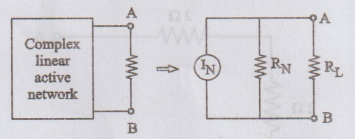
where

I_N → Short circuit current through AB

R_Th → Thevenin's Resistance

Explanation

To calculate I_N

For the given network, short circuit the load terminal and then measure the current passing through the load terminal that gives short circuit current (I_N) through AB.

To calculate R_th

1. Remove the load resistance R_L.

2. Short circuit the voltage source (Replace the voltage source by its internal resistance).

3. Open circuit the current source (Replace the current source by its internal resistances).

4. Then, measure the resistance at load terminal that gives the Norton's resistance (R_N).

Proof

Consider the given network consisting of voltage source V and resistors R₁, R₂, R₃ and R_L.

To measure the load current I_L, the given network is converted into its Norton's equivalent.

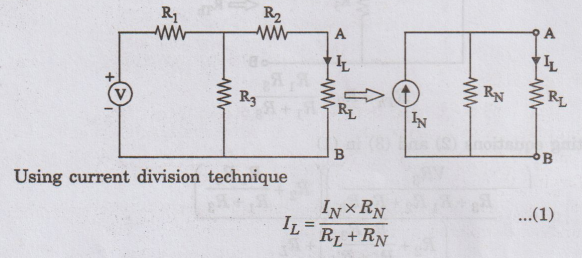
To calculate I_N

Short circuit the load terminal AB.

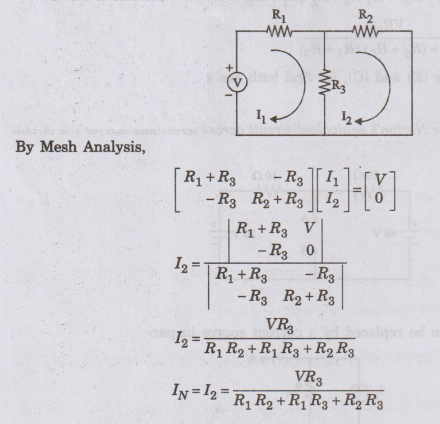
To calculate R_Th

Short circuit the voltage source 'V

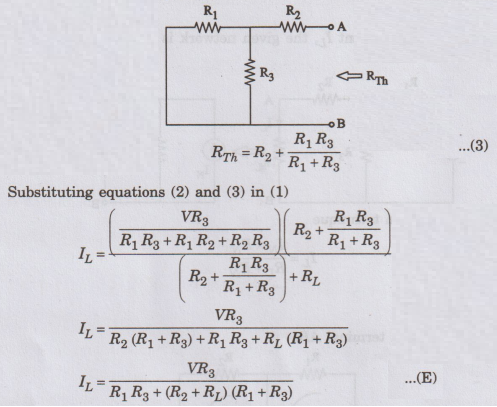
Comparing equations (E) and (C), we find both are same. Hence, the theorem is proved.

 

EXAMPLE 24: Determine Norton's equivalent circuit across terminals AB for the circuit shown in figure.

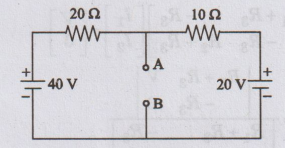
Solution:

The above circuit can be replaced by a current source in parallel with a resistor, as shown in figure.

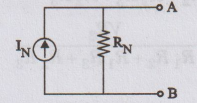
where

I_N = The current passing through the short circuited output terminals AB

R_Th = Norton's resistance

To find R_Th

Short circuit the voltage sources.

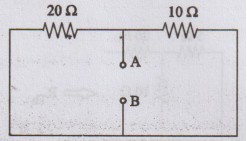
Here, 20 Ω and 10 Ω are connected in parallel.

R_Th = 20 × 10 / 20 + 10 = 6.66Ω

To find I_N

We have to find the current passing through the terminals A and B. It is shown in figure.

 

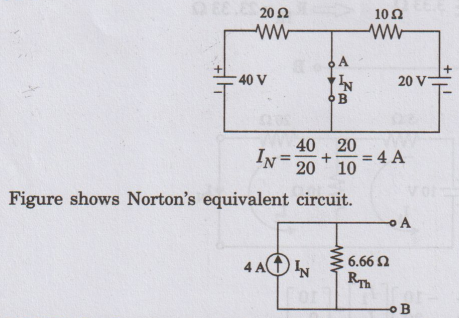
EXAMPLE 25: For the circuit shown in figure, find the current through the 30 22 load resistor using Norton's theorem.

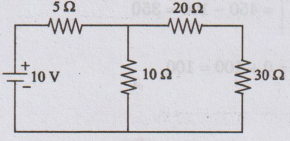
Solution :

Figure shows Norton's equivalent circuit.

To find R_Th

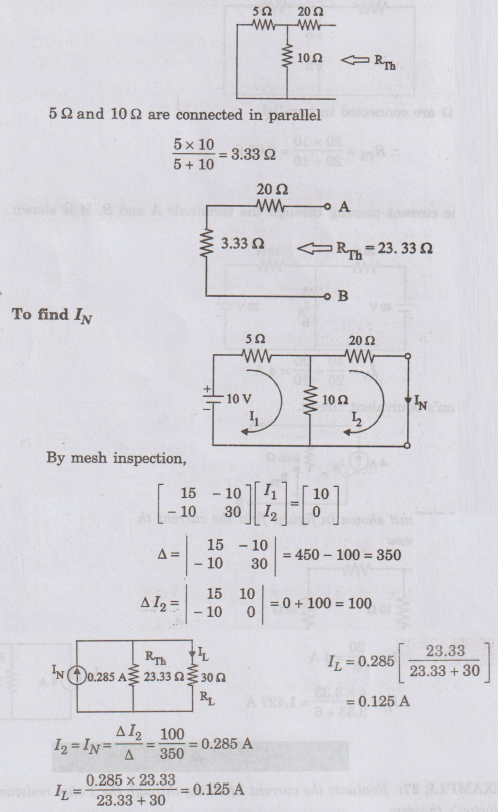
Current through 30Ω is 0.125 A

 

EXAMPLE 26: Using Norton's theorem, find current through 6 2 resistance shown in figure.

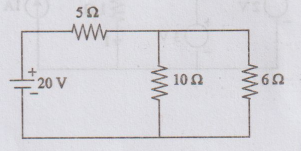
Solution:

Figure shows Norton's equivalent circuit.

To find R_Th

5Ω and 10 Ω are connected in parallel.

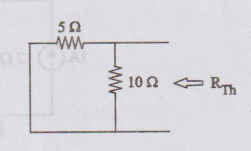
R_Th  = 5 × 10 / 5 + 10 = 3.33 Ω

To find I_N

No current in 10 Ω resistance because, it is short circuited.

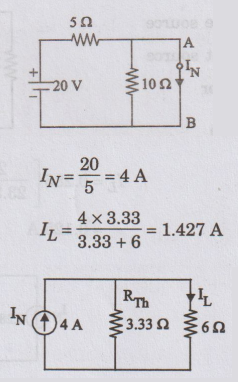
Current through 6 Ω is 1.427 A

 

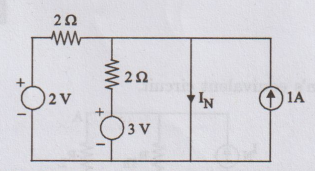
EXAMPLE 27: Evaluate the current I flowing through the 1 ohm resistance, by applying Norton's theorem.

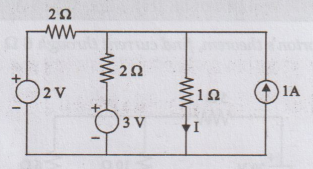
Solution:

To calculate I_N

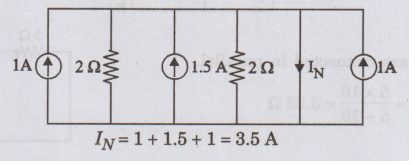
Convert the voltage sources into equivalent current sources

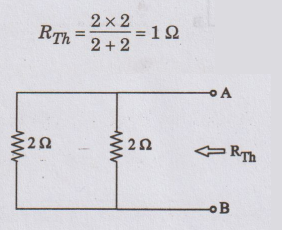
To calculate R_Th

→ Short circuit the voltage source

→ Open circuit the current source

→ Remove the load resistor

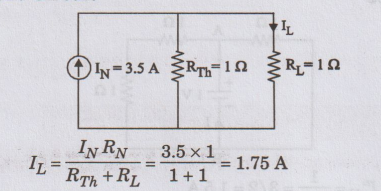
Norton's Equivalent Circuit

 

EXAMPLE 28: Determine the current through the resistance RL using Norton's theorem.

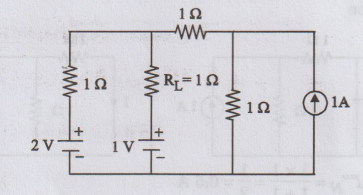
Solution:

To calculate R_Th

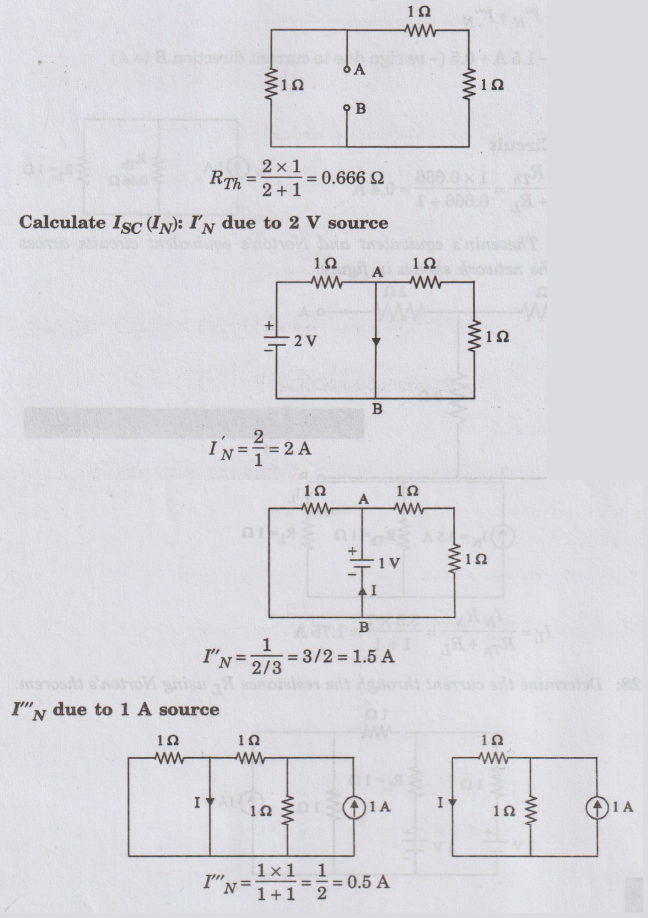
According to Superposition theorem

I_N = I_N + I"_N + I"_N

= 2A - 1.5 A + 0.5 (-ve sign due to current direction B to A)

I_N = 1A

Norton’s Equivalent Circuit

 

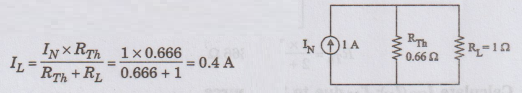
EXAMPLE 29: Obtain Thevenin's equivalent and Norton's equivalent circuits across terminals A and B for the network shown in figure.

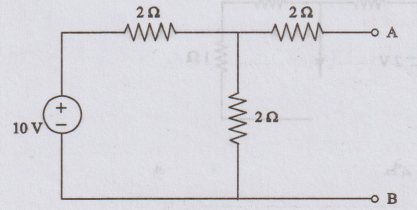
Solution:

(i) Thevenin's equivalent circuit:

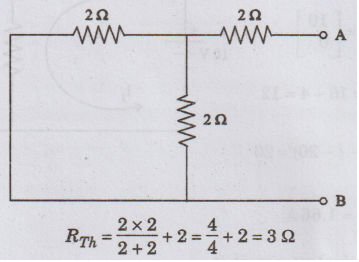
Thevenin's resistance R_Th

Short circuit the voltage source.

Thevenin's voltage V_oc

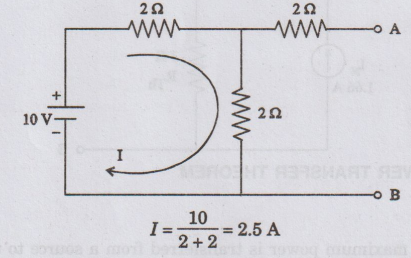
Voltage across AB = Voltage across 2Ω resistor = 2 × 2.5 = 5V

V_OC  = 5V

Thevenin's equivalent circuit is

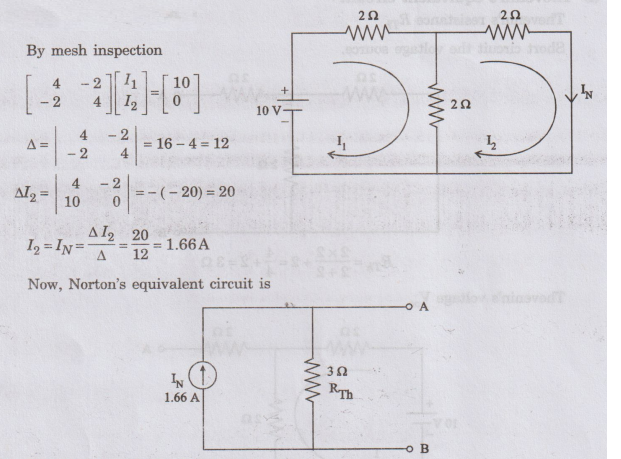
(ii) Norton's equivalent circuit:

R_Th = 3 Ω

Norton's current (I_N)

By mesh inspection