Oblique Incidence of Uniform Plane Waves

Oblique Incidence of Uniform Plane Waves

AU : June-07, Dec.-lO, 13,14

• When a uniform plane wave strikes obliquely on the surface (either conductor or dielectric), the behaviour of the reflected wave is decided by the polarization of the incident wave. There are two cases for the oblique incidence as given below.

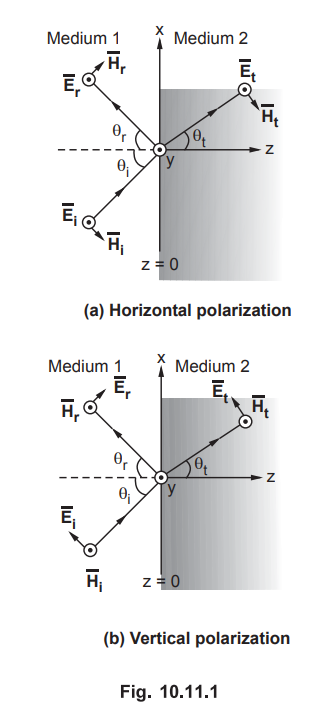
Case (i) : The electric field vector perpendicular to the plane of incidence. In other words, the electric field vector is aligned parallel to the boundary surface as shown in the Fig. 10.11.1 (a). This is called horizontal polarization.

Case (ii) : The magnetic field vector is aligned parallel to the boundary surface. In other words, the magnetic field vector is perpendicular to the plane of incidence while the electric field vector is aligned parallel to the plane of incidence as shown in the Fig. 10.11.1 (b). This is called vertical polarization.

• It is seen that, in both the cases, a new term 'plane of incidence' is used. What is meant by plane of incidence?

Key Point : A plane of incidence is a plane containing the vector in the direction of propagation of the incident wave and the normal to the boundary surface.

• The horizontal and vertical polarizations, illustrating two special cases are as shown in the Fig. 10.11.1 (a) and (b).

• Before we actually start discussing the different conditions for oblique incidence, let us take a review of most convenient way of expressing a uniform plane wave interms of direction cosines of the normal to the plane containing the wave. 

 

1. Direction Cosines

• According to the definition of a uniform plane wave, the wave for which the equiphase surface is a plane.

•  In general, any wave travelling in z-direction can be expressed in phasor form as

• For a wave travelling in positive z-direction, given by equation (10.11.1), the equiphase plane is given by equation,

z = a constant

• For a uniform plane wave travelling in any arbitrary direction, the equiphase surfaces can be obtained by replacing z with some expression. Thus the equation of a plane is given by,

• Let a uniform plane wave be travelling in some arbitrary direction say d. Let  be the unit vector normal to the plane P as shown in the Fig. 10.11.2. In the Fig. 10.11.2, positive x, y, z axes are considered. Also the plane which is perpendicular to , appears as a line P-P.

• We know that the projection of any vector in its normal direction is the dot product of that vector with unit vector in the normal direction. For all the points on the plane P, the distance OB remains constant. That means we can write

• Let  makes angles θ1 θ2 and θ3 with positive x, y and z axes respectively so cos θ1, cos θ2 and cos θ3 are the components of  along the positive x, y and z axes respectively.

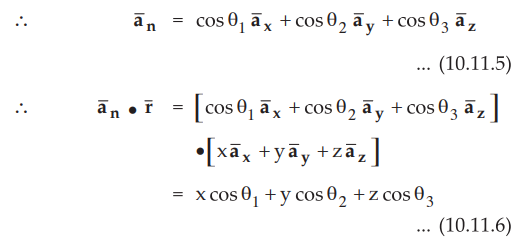
• Where cos θ1, cos θ2 and cos θ3 are called direction cosines of the vector.

• Now the equation of a uniform plane wave travelling in the direction d (i.e. in the direction of ) can be written as

 

2. Oblique Incidence at a Plane Conducting Boundary

• Consider an interface between a perfect dielectric and perfect conductor. As we have already studied that for oblique incidence there are two cases namely horizontal polarization and vertical polarization. Let us consider these two cases one by one.

a. Horizontal Polarization

• Consider that the plane wave is incident obliquely at the interface between a perfect dielectric and a perfect conductor, with the electric field vector  perpendicular to the plane of incidence as shown in the Fig. 10.11.3.

• As  

is perpendicular to the plane of incidence, this type of polarization is also called perpendicular polarization or E-polarization.

• The unit vector in the direction of incident wave is . Let θi be the angle of incidence. Then the unit vector is given by,

• Using the concept of direction cosines for equiphase surfaces, the equation of the incident wave can be written as

• The equation for incident magnetic field is given by,

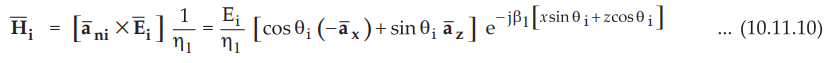
• For the reflected wave, the unit vector in the direction of the reflected wave is given by,

• Where θr is the angle of reflection.

• The electric field in the reflected wave is given by,

• As the medium 2 is perfect conductor, there will be no transmission. Hence according to the boundary condition, at the interface, z = 0, the total electric field intensity must be equal to zero.

• Thus at the interface, z = 0,

• To have equation (10.11.13) valid for all the values of x, Er must be equal to - Ej. At the same time, the phase terms of both the incident and reflected wave must be same. Thus the required condition is θr = θi which is called Snell's law of reflection.

• With above conditions, equation (10.11.12) can be written as,

• Now the total electric field intensity in medium 1,  can be obtained by adding equation (10.11.9) and equation (10.11.14).

• Similarly total magnetic field intensity in medium 1 can be obtained by adding equation (10.11.10) and equation (10.11.15).

• From equations (10.11.16) and (10.11.17), following conclusions can be drawn for perpendicular polarization with oblique incidence.

1. The y-component of , i.e. E_1y and the x-component of , i.e. H_1x represent standing waves generated in the z-direction which is normal to the boundary. These standing wave patterns can be recognized by the terms sin β z and cosβ z, where βz = β1 cos θ_i i.e. phase in z-direction in medium 1.

2. In the x-direction, both Eiy and Hlx are in phase with respect to time and space. Thus the phase velocity in x-direction in medium 1 is given by,

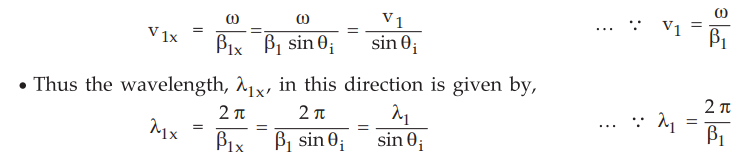
3. The amplitude of the wave varies with z in the x-direction, hence the wave propagating in x-direction is a non-uniform plane wave.

b. Vertical Polarization

• Consider that the plane wave is incident obliquely at the interface between a perfect dielectric and a perfect conductor, with the electric field vector  parallel to the plane of incidence as shown in the Fig. 10.11.4.

• As  is parallel to the plane of incidence, it is also called parallel polarization or H-polarization.

• The definitions of unit vectors  along with angles 01 and 0 r are the same as studied in E-polarization (or perpendicular polarization). From Fig. 10.11.4 it is clear that now the electric field intensities in the incident and reflected waves have components in x as well as z-directions. But the magnetic field intensity in the incident and reflected waves have components only in y-direction. Using the equations derived in earlier section, for the incident waves, we can write, 

• Again at the interface, z = 0, the tangential component of the electric field intensity must be zero. Note that, for parallel polarization, the tangential component of the electric field intensity is only x-component. Thus adding only x-components of the electric field intensity from equation (10.11.18) and equation (10.11.20), we get,

• Similarly, the total magnetic field intensity in medium can be obtained by adding equations (10.11.19) and (10.11.21),

• From equations (10.11.22) and (10.11.23), following conclusions can be drawn for parallel polarization for oblique incidence.

1. The x-component of  i.e. H_1y represent standing waves generated in the z-direction. Similar to the previous case of horizontal polarization, these standing wave patterns are recognized by the terms sin β₁z and cos β₁z .

2. Both the components E1z and H1y are in phase with time and space in x-direction. The velocity in this direction is given by,

v_1x = v1 / sin θ_i

Similarly the wavelength of the wave in the same direction is given by,

λ_lx = λ₁ / sin θ_i

3. The wave propagating in x-direction is a non-uniform plane wave.

 

3. Oblique Incidence at a Plane Dielectric Boundary

• In the last section, we discussed the oblique incidence at a plane conducting boundary. Now consider that a uniform plane wave is incident obliquely at the interface between the two dielectrics. The two dielectric media are assumed to be lossless with different constants. Such as µ₂, Ɛ₂ for medium 1 while g2, e2 for medium 2. As the two media are having different constitutive parameters, at the boundary, thus there is as if discontinuity. Because of this, at the interface, a part of the incident wave is reflected; while a part is transmitted as shown in the Fig. 10.11.5.

• Let the lines OA, O'A' and O'B be the intersections of the plane of incidence with the equiphase surfaces of the incident, reflected and transmitted waves respectively. The incident and reflected waves travel in medium 1, while transmitted wave in medium 2. The velocity for the waves in medium 1 is same say v₁. Then distances 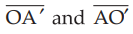 must be same.

 

• From equation (10.11.24) it is clear that the angle of incidence and angle of reflection are equal. This is nothing but Snell’s law of reflection.

• It is also observed the time taken by the incident wave to travel from A to O' in medium 1 is equal to that taken by the transmitted wave to travel from O to B in medium 2. Thus we can write,

• Where v₁ is the velocity of the wave in medium 1 while v₂ is velocity of the wave in medium 2.

• Simplifying above equation,

• But for any medium, the ratio of the speed of light in free space to that in medium is called index of refraction. It is denoted by n and it is given by,

n = c / v

where c = Velocity of light in free space

v = Velocity of light in medium

• Then for medium 1, index of refraction is given by,

n₁ = c /v₁

Similarly, for medium 2, index of refraction is given by,

n₂ = c /v₂

• Substituting values of v₁ and v₂ mterms of n₁ and n₂ in equation (10.11.25), we get,

sin θ_t / sin θ_i = n₁/ n₂ 

• Equation (10.11.26) represents Snell’s law of refraction.

• For a non-magnetic media, µ1 = µ2 = µ0.

• Then we can write velocities as, 

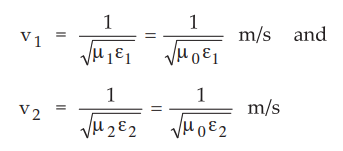
• Putting the values v₁ and v₂ in equation (10.11.25), we get,

• Also we know, the intrinsic impedances for both the media are different. These impedances can be expressed as follows.

• Rearranging the terms in equation (10.11.27),

a. Total Reflection

• Consider that medium 1 is denser as compared to medium 2 i.e. Ɛ1 > Ɛ2. Under this condition the angle of transmission 91 becomes greater than the angle of incidence. The angle of transmission 91 increases with angle of incidence θ_i. When θ_t = π/2, the transmitted wave will be aligned along the interface as shown in the Fig. 10.11.6.

• If θ_i is increases further, then there will be no transmitted wave and the condition is named as total reflection. The angle of incidence at which the total reflection takes place is called critical angle (θ_c)

• Then at θ_t = π/2, θ_i = θ_c, equation (10.11.27) becomes,

 

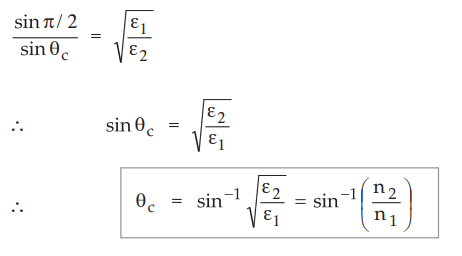
Ex. 10.11.1 An electromagnetic wave from an underwater source with perpendicular polarization is incident on a water air interface. Find critical angle  θ_c if for fresh water Ɛr = 81, µr = 1

Sol. : The critical angle is given by,

 • From the discussion in the previous section, it is clear that Snell's law of refraction and the critical angle calculation are independent of type of polarizations. But to derive the formulae for the transmission coefficient and reflection coefficient, we have to consider two special cases of the polarizations namely horizontal (perpendicular) polarization and vertical (parallel polarization).

b. Horizontal Polarization (Perpendicular Polarization)

• Consider that a uniform plane wave is incident obliquely with   perpendicular to the plane of incidence as shown in the Fig. 10.11.7.

• Using the concept of direction cosines, we can now easily write the field intensity vectors in any medium.

• The incident electric field intensity vector, in medium 1, is given by,

• Similarly the incident magnetic field intensity vector is given by,

From the Fig. 10.11.7, it is clear that a wave is transmitted in medium 2. Thus, in medium 2, the field vectors are given as follows :

• As we know, from boundary conditions, the tangential components of E and H must be continuous at the interface, z = 0.

• Thus for the electric field intensity  and , we can write, at z = 0,

• To have the phase matching for all x, the exponential factors which are functions of x are equal in both the equations (10.11.36) and (10.11.37). This requirement gives condition,

β₁ x sinθ_i = β₁ x sinθ_r = β₂ x sinθ_t ...(10.11.38)

• The condition stated above illustrates,

i) Snell's law of reflection (θ_i = θ_r) and

ii) Snell's law of refraction(sin θ_t / sin θ_i = β₁ / β₂ )

Now equation (10.11.36) can be written as,

E_i + E_r = E_t ... (10.11.39)

• Similarly equation (10.11.37) can be written as,

1 / ɳ₁ (Ei - Er) cos θ_i = Et / ɳ₂ cos θ_t … (10.11.40)

• Simplifying equations (10.11.39) and (10.11.40), the transmission coefficient with perpendicular polarization is given by,

• Similarly, the reflection coefficient, for perpendicular polarization is given by,

Similar to the condition for the normal incidence, for the oblique incidence we can write,

c. Vertical Polarization (Parallel Polarization)

• Consider that a uniform plane wave, with Ē parallel to the plane of incidence, is incident obliquely as shown in the Fig. 10.11.8.

• The incident electric and magnetic field intensity vectors, in medium 1, are given by,

…. (10.11.44)

• Similarly for the reflected wave, the electric and magnetic field intensity vectors are given by,

• Now in medium 2, the transmitted electric and magnetic field intensity vectors are given by,

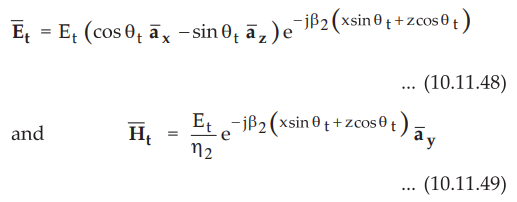
• Similar to the horizontal polarization, using boundary conditions, the tangential components of   and  are continuous at the boundary.

• Thus we can write,

• Solving equations (10.11.50) and (10.11.51), for the parallel polarization, the transmission coefficient is given by,

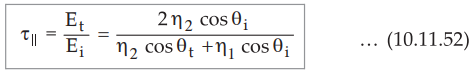
• Similarly, for parallel polarization, the reflection coefficient is given by,

• From equations (10.11.52) and (10.11.53), the relation between τ_|| and ɼ_|| is given by,

• The condition for no reflection occurs when τ_|| = 0. Thus for no reflection, the numerator in equation (10.11.53) must be zero, which gives

According to Snell's law of refraction,

• Where n₁ and n₂ are the refractive indices. Thus we can write,

• Here angle θ_i is called Brewster angle for parallel polarization and it is denoted by θ_B. When θ_i = θ_B for parallel polarization, no reflection takes place. For non-magnetic media only the equation (10.11.56) is valid. For non-magnetic media µ1 = µ2. Then the no reflection condition is modified as,

• The alternative formula for the Brewster angle is given by,

Then Brewster angle θ_B is given by,

• The significance of Brewster angle is that, when an unpolarized wave is incident obliquely at the Brewster angle θ_B, only the component with perpendicular polarization will be reflected ; while component with parallel polarization will not be reflected. Hence it is also referred as polarizing angle.

 

Ex. 10.11.2 A parallel polarized wave propagates from air to a dielectric at Brewster angle of 75°. Find Ɛr.

Sol. : A parallel polarized wave travels from air (medium-1) to a dielectric (medium-2).

For air, Ɛ₁ = Ɛ_r1 Ɛ₀ = Ɛ₀ as Ɛ _r1 =1

For dielectric, Ɛ₂ = Ɛ_r2 Ɛ₀

Brewster angle θ_B =75°

The Brewster angle is given by,

 

Ex. 10.11.3 Determine the critical angle for the electromagnetic wave passing through glass to air if er for glass is 9.

Sol. : Medium 1 is glass, for which Ɛ_r1 = 9 ; while medium 2 is air, for which Ɛ_r2 = 1.

The critical angle is given by,

 

Ex. 10.11.4 A uniform plane wave in air with  is incident on a dielectric slab (z ≥ 0) with µr = 1.0, σ = 0. Ɛr = 2.5. find : a) Polarization of wave b) The angle of incidence c) The transmitted  field.

AU : June-07

Sol. : i) From the given expression of   field , it is clear that, the propagation vector is,

As unit vector normal to interface at z = 0 is , the plane consisting  plane and it is a plane of incidence. As  is normal to this plane, the wave polarization is perpendicular polarization.

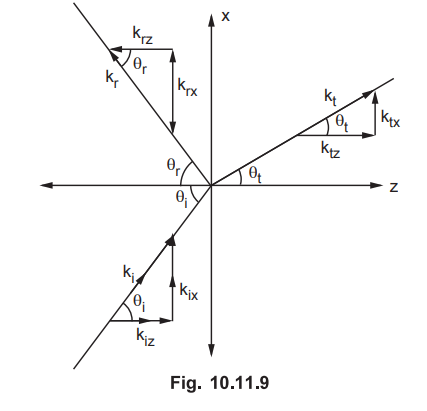
ii) Let us refer following Fig. 10.11.9 which illustrates all propagation vectors.

From Fig. 10.11.9.

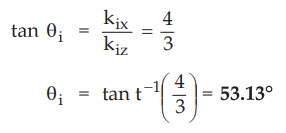
Thus the angle of incidence is θ_i = 53.13°

iii) Let us assume that the reflected electric field component be

Not that  unit vector indicates that the tangential component

of  is continuous at interface.

But by property, θ_i = θ_r  and k_i = k_r. Hence we can write

 

Hence the reflection coefficient for the perpendicular polarization is given by,

Thus the transmission coefficient for perpendiculaqr polarization is given by,

 

Examples for Practice

Ex. 10.11.5 An electromagnetic wave travelling in free space is incident on a dielectric medium with relative permeability equal to 2 at an angle of 45°. Find the angle bp which  tilts as wave crosses the boundary ?

[Ans.: 30°]

Ex. 10.11.6 An EM wave travelling in a dielectric medium having dielectric constant 9 is incident at an angle on the dielectric-air interface.

Determine :

i) Critical angle ii) Reflection coefficient for perpendicular polarization. If the angle of incidence is 15°.

[Ans. : 19.47° 125.578  4.95° 0.744]

Ex. 10.11.7 A light is incident from air to glass at Brewster’s angle. Determine the incident and transmitted angles.

[Ans. : 71.565° 9i = 71.565 ° 18.434°

Review Questions

1. Define Brewster angle and derive its expression.

AU : Dec.-10, 13, Marks 16

2. Define plane of incidence. Explain in brief direction cosines.

3. What do we mean when we say that an incident wave has

a) Perpendicular polarization b) Parallel polarization.

4. Explain Snell's law of reflection and Snell's law of refraction.

5. What is total reflection in case of oblique incidence at a plane dielectric boundary ? What is critical angle θc ? Derive the express ion for θc.

6. Derive the expressions for reflection coefficient and transmission coefficient for a obliquely incident wave having

i) Perpendicular polarization

ii) Parallel polarization.

7. Write a note on Brewster angle.

8. Briefly explain about the wave incident obliquely to the surface of perfect conductor.

AU : Dec.-14, Marks 8