One Way Classification

ONE WAY CLASSIFICATION

One-way classification observations are classified according to one factor. This is exhibited column-wise.

A set of N = cr observations classified in one direction may be represented as follows.

If each of these sum of squares is divided by the corresponding number of degrees of freedom, we get the mean sum of squares. These information are presented in the following table called ANOVA table.

(Analysis of Variance Table)

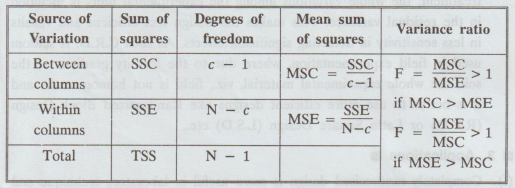
The F ratio should be calculated in such a way that F > 1.

Completely Randomized Design (C.R.D)

The completely randomized design is the simplest of all the designs, based on principles of randomization and replication. In this design, treatments are allocated at random to the experimental units over the entire experimental material.

 

1. Merits

(i) C.R.D. results in the maximum use of the experimental units, since all the experimental material can be used.

(ii) The design is very flexible. Any number of treatments can be used and different treatments can be used unequal number of times without unduly complicating the statistical analysis in most of the cases.

(iii) The statistical analysis remains simple, if some or all the obsevations for any treatment are rejected or lost or missing for some purely random accidental reasons. We merely carry out the standard analysis on the available data. Moreover, the loss of information due to missing data is smaller in comparison with any other design.

(iv) It provides the maximum number of degrees of freedom for the estimation of the error variance, which increases the sensitivity or the precision of the experiment for small experiments, (i.e.,) for experiments with small number of treatments.

 

2. Demerits

(i) In certain circumstances, the design suffers from the disadvantage of being inherently less informative than other more sophisticated layouts. This usually happens, if the experimental material is not homogeneous. Since randomization is not restricted in any direction to ensure that the units receiving one treatment are similar to those receiving the other treatment, the whole variations among the experimental units is included in the residual variance. This makes the design less efficient and results in less sensitivity in detecting significant effects. As such C.R.D. is seldom used in field experimentation, where due to the fertility gradient of the soil, the whole experimental material, viz., field is not homogeneous and it is better to use more efficient designs like Randomized Block Design (R.B.D) or Latin Square Design (L.S.D) etc.,

 

3. Applications

(i) Completely randomised design is more useful in laboratory technique and methodological studies, (e.g.,) in physics, chemistry or cookery, in chemical and biological experiments, in some green house studies, etc., where either the experimental material is homogeneous or the intrinsic variability between units can be reduced.

(ii) C.R.D is also recommended in situations where an appreciable fraction of units is likely to be destroyed or fail to respond.

Working Procedure [One-way classification CRD]

1. H_o: There is no significant difference between the treatments.

2. H₁: There is significant difference between the treatments.

Step 1: Find N i.e., the number of observations

Step 2: Find T i.e., the total value of all observations

Step 3: Find T² / N i.e., the correction factors lea

Step 4: Calculate the total sum of squares.

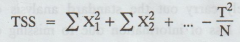
Step 5: Calculate the column sum of squares

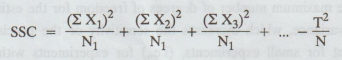
Step 6: Calculate the error sum of squares

SSE = TSS - SSC

Step 7: ANOVA

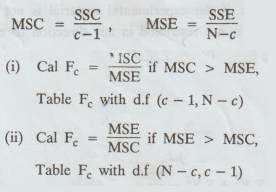
Step 8: Conclusion :

(i) If Cal F_e < Table F_e, we accept H₀

(ii) If Cal F_e > Table F_e, we reject H₀

 

Example 2.2.1

The following are the numbers of mistakes made in 5 successive days of 4 technicians working for a photographic laboratory :

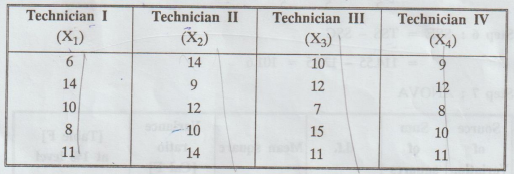
Test at the level of significance a=0.01, whether the differences among the 4 sample means, can be attributed to chance. [A.U. A/M 2004, A.U A/M 2011]

Solution:

H₀ : There are no significant differences in technicians.

H₁ : There is significant difference between the technicians.

We shift the origin to 10.

Step 8: Conclusion: Cal Fe'< Tab Fe i.e., 1.47 < 26.9

So, we accept H₀

i.e., There are no significant differences in technicians at 1% level of significance.

 

Example 2.2.2

There are three main brands of a certain powder. A set of 120 sample values is examined and found to be allocated among four groups (A, B, C and D) and three brands (I, II, III) as shown here under : [A.U. A/M. 2004]

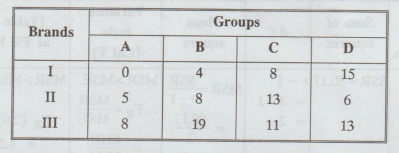
Is there any significant difference in brands preference? Answer at 5% level.

Solution :

H₀ :  There are no significant differences in brands.

H₁ : There is significant difference in brands.

Example 2.2.3

A completely randomised design experiment with 10 plots and 3 treatments gave the following results : [A.U. N/D 2007]

Analyse the results for treatment effects.

Solution :

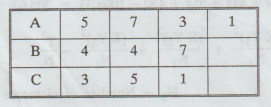
H₀ : There are no significant differences in treatments.

H₁ : There is significant difference in treatments.

Step 8: Conclusion:

Cal F <  Table F

i.e., 1.62 < 19.35

So, we accept H₀

There are no significant differences in treatments.

 

Example 2.2.4

The following table shows the lives in hours of four brands of electric lamps.

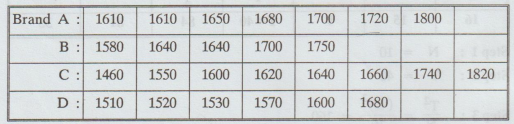
Perform an analysis of variance test the homogneity of the mean lives of the four brands of Lamps. [A.U. A/M. 2008] [A.U N/D 2011] [A.U Tvli M/J 2011] [A.U A/M 2015 R-13]

Solution:

H₀ : There are no significant differences in brands.

H₁ : There is a significant difference between the four brands.

Subtract 1600 and then divided by 10, we get

Step 8: Conclusion: Cal Fe < Table Fe

i.e., 2.21 < 3.05

So, we accept H₀

The lives of the four brands of lamps do not differ significantly.

 

Example 2.2.5

The accompanying data resulted from an experiment comparing the degree of soiling for fabric co-polymerized with the three different mixtures of methacrcylic acid. Analysis is the given classification. [A.U A/M 2017 R-13] [A.U N/D 2019 R-13] 

Solution :

H₀ : The true average degree of soiling is identical for three mixtures.

H₁ : The true average degree of soiling is not identical for three mixtures.

Step 8: Conclusion: Cal Fe < Tab Fe.

i.e., 1.0132 < 19.41

So, we accept H₀.

The true average degree of soiling is identical for three mixtures.

 

Example 2.2.6

The table shown below gives the samples got from normal population with equal variances. Test the hypothesis that the sample means are equal to 5% and 1% levels.

Solution :

H₀ : There is no significant difference in the means of samples.

H₁ : There is significant difference in the means of samples.

Subtract 10 from each figure.

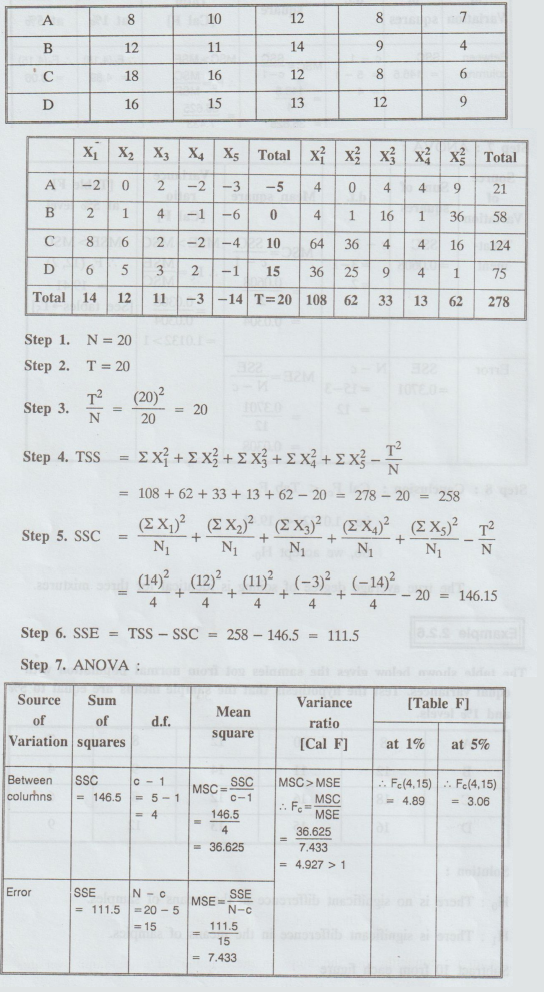
Step 8. Conclusion:

 (i) Cal F > table F, i.e., 4.927 > 3.06

So, we reject Ho at 5% level of significance.

(ii) Cal F > table F, i.e., 4.927 > 4.89

So, we reject Ho at 1% level of significance.

 

EXERCISE 2.2

[One Way Classification]

1. The three samples given below have been obtained from three normal populations with equal variances. Test the hypothesis that the population means are equal at 5% level of significance.

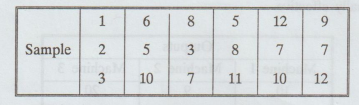
2. The following data give the yields, of 12 plots of land in three samples, each of 4 plots, under three varieties of fertilizer A, B and C.

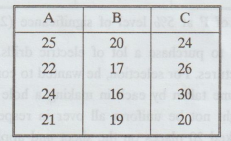
Is there any significant difference in the average yields of land, under the three varieties of fertilizers ?

3. Weekly sales in Rs., in small shops in 3 towns, A, B and C are as follows.

Can we conclude that the shops in the 3 towns have the same average sales? Given F05 (2, 9) = 4.26.

4. Three samples of size 5 each were drawn from three uncorrelated normal populations with equal variances. Test the hypothesis that the population means are equal at 5% level.

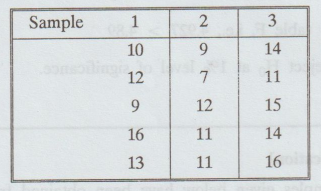
5. Three different machines are used for a production. On the basis of the outputs, set up one-way ANOVA table and test whether the machines are equally effective.

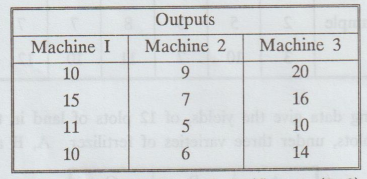
Given that value of F at 5% level of significance (2, 9) df = 4.26.

6. A person wanted to purchase a lot of electric drills. He got quotations from five manufactures. For selection, he wanted to conduct an experiment to estimate the time taken by each in making a hole in a metallic sheet. As the sheet might not be uniform all over in respect of thickness and hardness, he marked 20 places on the sheet and applied four drills from each concern in 4 randomly selected places to make holes. The time for marking each hole was recorded and these formed the observations. The observations in seconds are shown below in brackets along with marks. of the drills denoted by D₁, D₂, D₃ , D₄ and D₅.

Analyse, the given data.

7. A car rental agency, which uses 5 different brands of tyres in the process ni)n of deciding the brand of tyre to purchase as standard equipment for its o fleet, finds that each of 5 tyres of each brand last the following number 20.0 of kilometers (in thousands) but is

Tyre brands

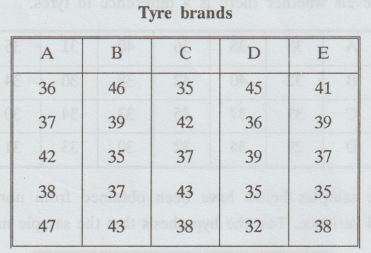
Test the hypothesis that the five tyre brands have almost the same average life.

8. In order to determine whether there is significant difference in the durability of 3 makes of computers, samples of size 5 are selected from each make and the frequency of repair during the first year of purchase 1300 is observed. The results are as follows:

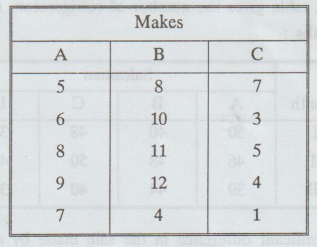
In view of the above data. What conclusion you draw?

9. Table show the milk production of arbitrary units in four days with three different cattle feed A, B and C. Analyse the results of cattle-feed brands.

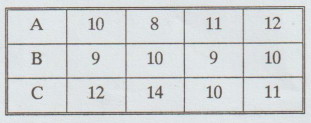
10. A company wishes to test four different types of tyres A, B, C and D. The life time of the tyres, as determined from their treads, are given (in Todm thousands of miles) in the table, where each type has been tried on 6 similar automobiles assigned at random to tyres. Test at the (i) 0.05 (ii) 0.01 levels whether there is a difference in tyres.

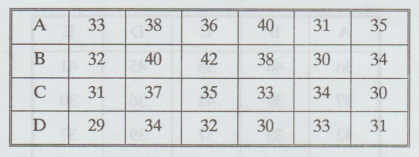
11. The three samples below have been obtained from normal population with equal variance. Test the hypothesis that the sample means are equal:

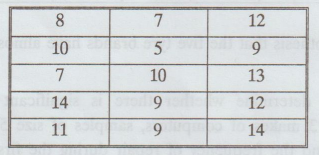
12. The following table gives the number of refrigerators sold by 4 salesman in three months :

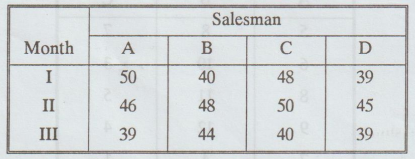
Is there a significant difference in the sale made by the four salesman? ods.

Is there a significant difference in the sales made during different month? lim od [A.U. N/D 2006]