Op-amp Integrator

Integrator

May-03,04,07,08,09,10,11,12,15, Dec.-06,08,09,ll,14

In an integrator circuit, the output voltage is the integration of the input voltage. The integrator circuit can be obtained without using active devices like op-amp, transistors etc. In such a case an integrator is called passive integrator. While an integrator using an active devices like op-amp is called active integrator. In this section, we will discuss the operation of active op-amp integrator circuit.

 

1. Ideal Active Op-amp Integrator

Consider the op-amp integrator circuit as shown in the Fig. 2.29.1.

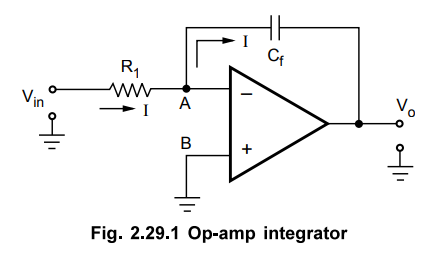
The node B is grounded. The node A is also at the ground potential from the concept of virtual ground.

V_A = 0 = V_B

As input current of op-amp is zero, the entire current I flowing through R₁, also flows through C_f, as shown in the Fig. 2.29.1.

where V_o (0) is the constant of integration, indicating the initial output Voltage.

The equation (2.29.5) shows that the output is - 1/ R₁ C_f times the integral of input and R₁ C_f is called time constant of the integrator.

The negative sign indicates that there is a phase shift of 180° between input and output. The main advantage of such an active integrator is the large time constant. By Miller's theorem the effective capacitance between input terminal A and the ground becomes C_f (1-A_v ) where A_v is the gain of the op-amp which is very large. Due to such large effective capacitance, time constant is very large and thus a perfect integration results due to such circuit.

Sometimes a resistance R_comp = R₁ is connected to the non-inverting terminal to provide the bias compensation. This is shown in the Fig. 2.29.2.

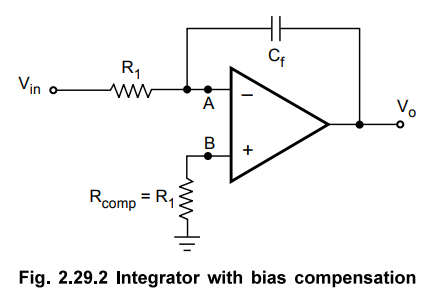
As the input current of op-amp is zero, the node B is still can be treated at ground potential in this circuit.

Key Point Hence the above analysis is equally applicable to the integrator circuit with bias compensation. And the output is the perfect integration of the input.

 

2. Input and Output Waveforms

Let us see the output waveforms, for various input signals. For simplicity of understanding, assume that the time constant  R₁C_f = 1 and the initial voltage V_o (0) = 0V

i) Step input signal

Let the input waveform is of step type, with a magnitude of A units as shown in the Fig. 2.29.3

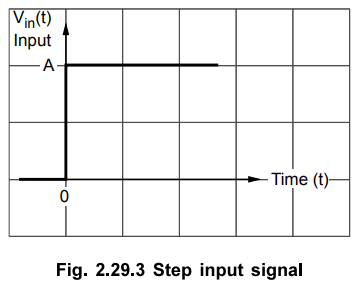
Mathematically the step input can be expressed as,

V_in (t) = A for t  ≥ 0

And   = 0 for t ≤ 0

From equation (2.29.5), with R₁C_f = 1 and V_o(0) = 0,

We can write,

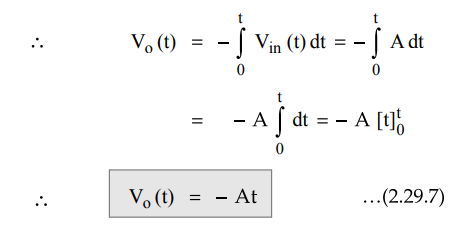
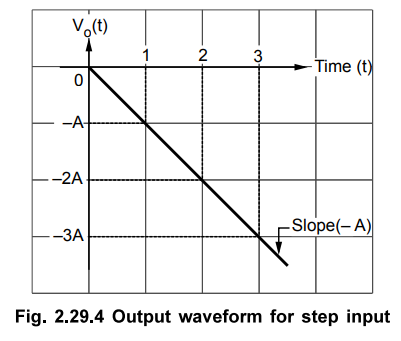
Thus output waveform is a straight line with a slope of -A where A is magnitude of the step input. The output waveform is shown in the Fig. 2.29.4.

ii) Square wave input signal

Let the input waveform is a square wave as shown in the Fig. 2.29.5

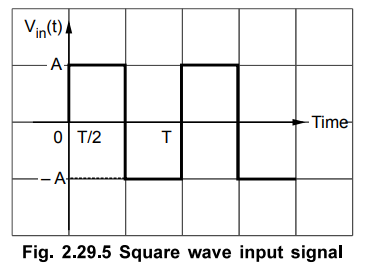
It can be observed that the square wave is made up of steps i.e. a step of A between time period of 0 to T/2 while a step of - A units between a time period of T/2 to T and so on.

Mathematically it can be expressed as,

V_in(t)= A, 0 < t < T/2  ….. (2.29.8)

= - A, T/2 < t < T

This is the expression for the input signal for one period.

As discussed earlier, the output for step input is a straight line with a slope of -A. So for the period 0 to T/2 output will be straight line with slope - A. From t = T/2 till t = T, the slope of the straight line will become - (-A) i.e. + A.         

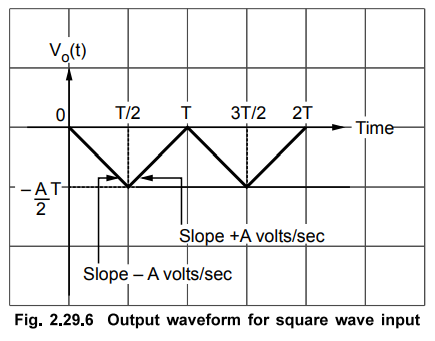
So the output can be expressed Fig. 2.29.6 Output waveform for square wave input mathematically for one period as,

V_o(t)= - A t 0 < t < T/2 

= + A t T/2 < t < T  ….. (2.29.9)

The output waveform is shown in the Fig. 2.29.6.

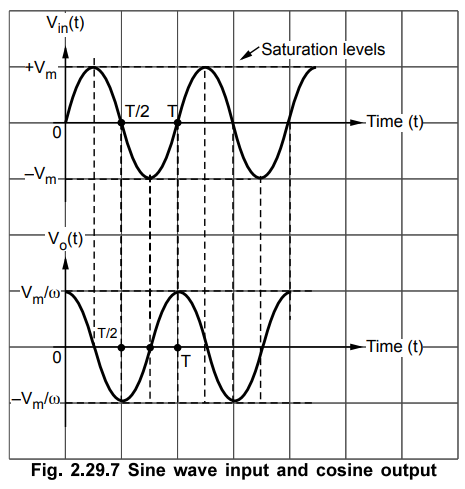
iii) Sine wave input signal

Let the input waveform is purely sinusoidal with a frequency of co rad/sec. Mathematically it can be expressed as,

V_in (t) = V_m Sin ω t ... (2.29.10)

where V_m is the amplitude of the sine wave and T be the period of the waveform.

To find the output waveform, use the equation (2.29.5) with R₁C_f = 1 and V_o(0) = 0 V.

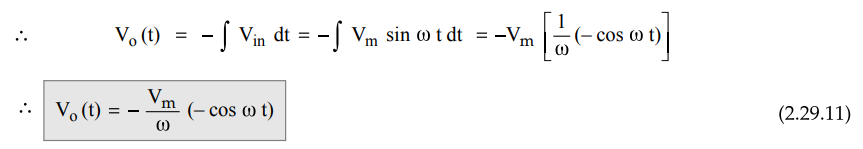
Thus it can be seen that the output of an integrator is a cosine waveform for a input. Due to inverting integrator, the output waveform is as shown in the Fig. 2.29.7.

 

3. Errors in an Ideal Integrator

The operation amplifier has input offset voltage (V_ios) and the input bias current (Ib)- In the absence of input voltage or at zero frequency (d.c.), op-amp gain is very high. The input offset voltage gets amplified and appears at the output as an error voltage. The bias current also results in a capacitor charging current and adds its effect in an output error voltage.

The two components, due to high d.c. gain of op-amp cause output to ramp up or down, depending upon the polarities of offset voltage and/or bias current. After some time, output of op-amp may achieve its saturation level. Hence there is a possibility of op-amp saturation due to such an error voltage and it is very difficult to pull op-amp out of saturation. Thus the output of an ideal integrator in the absence of input signal is likely to be offset towards the positive or negative saturation levels.

In the presence of the input signal also, the two components namely offset voltage and bias current, contribute an error voltage at the output. Thus it is not possible to get a true integration of the input signal at the output. Output waveform may be distorted due to such an error voltage.

Another limitation of an ideal integrator is its bandwidth, which is very small. Hence an ideal integrator can be used for a very small frequency range of the input only. 

Due to all these limitations, an ideal integrator is not used in practice. Some additional components are used along with the basic integrator circuit to reduce the effect of an error voltage, in practice. Such an integrator is called Practical Integrator Circuit.

 

4. Practical Integrator

The limitations of an ideal integrator can be minimized in the practical integrator circuit, which uses a resistance R_f in parallel with the capacitor C_f.

The practical integrator circuit is shown in the Fig. 2.29.8.

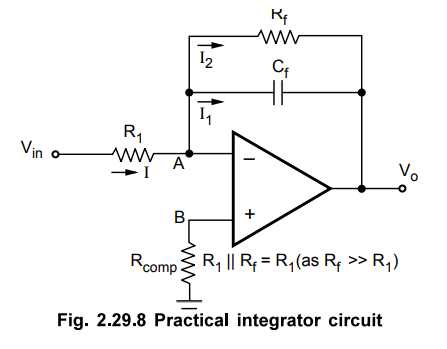
The resistance R_comp is also used to overcome the errors due to the bias current.

The resistance R_f reduces the low frequency gain of the op-amp.

 

5. The Analysis of Practical Integrator

As the input current of op-amp is zero, the node B is still at ground potential. Hence the node A is also at the ground potential from the concept of virtual ground.

So V_A = 0.

When R_f is very large then R₁/R_f can be neglected and hence circuit behaves like an ideal integrator as,

 

6. Frequency Response of Practical Integrator

To determine the frequency response, let us obtain the expression for the gain of the practical integrator interms of the frequency.

From the equation (2.29.18) we can write,

This is the break frequency or the comer frequency of the practical integrator. Thus in the frequency response, d.c. gain remains constant for all frequencies less than f_a and from the frequency f_a onwards, as frequency increases, gain reduces at a rate of 20 dB/decade.

The magnitude of the gain A is,

Thus an infinite d.c. gain of op-amp in case of an ideal integrator, gets limited to R_f /R₁ in the practical integrator.

Similarly at f = f _a we get,

Thus the magnitude of gain drops by 3 dB at the frequency f = fa which is R 60 the break frequency. Now for the integration, the frequency response must be straight line of slope -20 dB/decade, which is possible for the frequencies greater than fa and less than fb. Thus in between and practical integrator acts as an integrator. Below fa, integration does not take place. The frequency response is shown in the Fig. 2.29.9

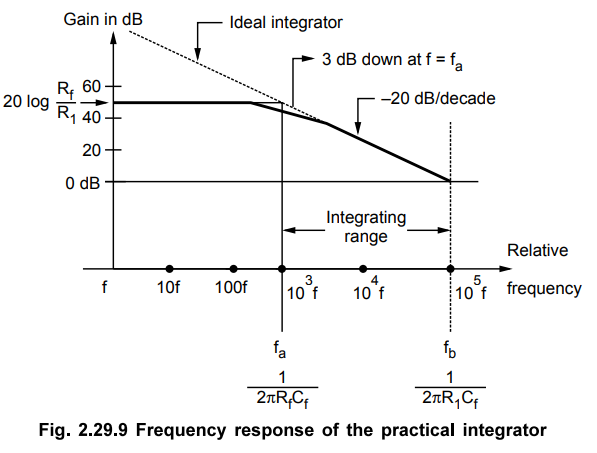
Key Point It can be seen from the frequency response that the bandwidth of practical integrator is f a which is much higher than an ideal integrator.

B.W. of Practical Integrator = f_a  … (2.29.30)

For any input bias current or current due to offset voltage, the path of current is through Rf rather than through the capacitor Cf. Thus the output voltage is decided by the resistance ratio (R_f/ R₁) which is typically selected as ≥ 10. For (R_f/ R₁) of 10, the frequency f_a becomes (f_b/10), this ensures the true integration of the input signal.

For proper integration, the time period T of the input signal has to be larger than or equal to RfC_f, so

T ≥ R_fC_f      ... (2.29.31)

where  R_fC_f  = 1 / 2π f_a

The practical integrator circuit is also called lossy integrator as it behaves as integrator only over the upper frequency range.

 

7. Applications of Practical Integrator

The integrator circuits are most commonly used in the following applications :

a) In the analog computers,    

b) In solving the differential equations,

c) In analog to digital converters.     

d) Various signal wave shaping circuits,

e) In ramp generators.

 

8. Why Integrators are Preferred in Analog Computers ?

It is important to note that the differentiators are avoided in the analog computer while integrators are widely used in the analog computers. Let us see the reasons why the integrators are preferred in the analog computers.

i) The gain of the integrator decreases with increase in the frequency while that of the differentiator increases with increase in the frequency. Hence it is very easy to stabilise the integrator with respect to the spurious oscillations.

ii) The input impedance of the integrator is constant and not a function of frequency. While the input impedance of the differentiator decreases as the frequency increases. So at high frequency the input impedance is very small. If the input waveform changes rapidly then due to small input impedance, there is every possibility that the amplifier of the differentiator gets overloaded.

iii) The differentiator has a tendency to amplify the noise and drifts which may result in the oscillations. The bandwidth of an integrator is small hence the integrator is less sensitive to noise voltages.

iv) The initial voltages present at the output before integration takes place are called as initial conditions. It is very easy to introduce the initial conditions in the integrator rather than the differentiator. 

v) Overall the integrator is more stable than the differentiator and less sensitive to noise and hence chances of oscillations are much less in the integrator.

Due to all these reasons the integrators are preferred in the analog computers.

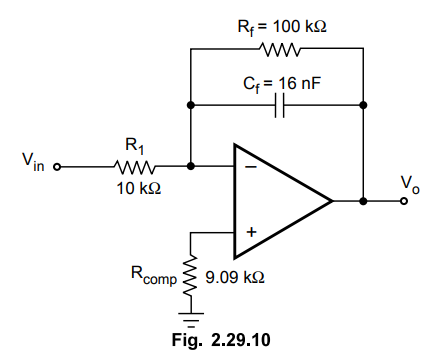
Example 2.29.1 Design a practical integrator circuit with a d.c. gain of 10, to integrate a square wave of 10 kHz.

Solution : The d.c. gain for the practical integrator is

|A| d.c. = R_f / R₁ i.e. 10 = R_f / R₁

The input frequency is f = 10 kHz.

Now for the proper integration f  ≥ 10 fa where fa is the break frequency of the practical integrator.

Hence the practical integrator circuit is as shown in the Fig. 2.29.10.

Example 2.29.2 Plot to scale the output waveform of the circuit shown in Fig. 2.29.11

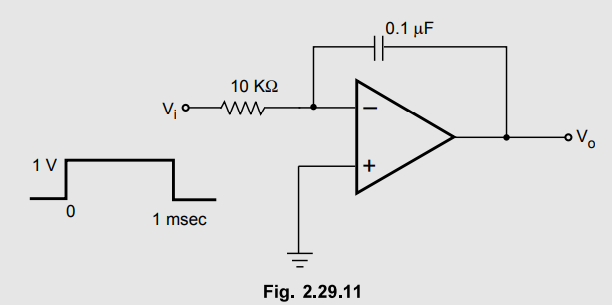
Solution :  The given circuit is an integrator with R1 = 10 kΩ and C = 0.1 µF.

 

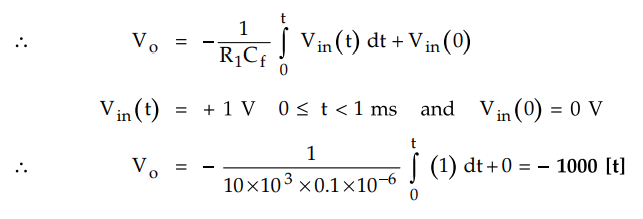
Thus V_o is a straight line of slope - 1000 till 1 ms.

At t = 1 ms,

V_o = -1000 × 1 × 10^-3 = -1V. This acts as an initial voltage for next integration.

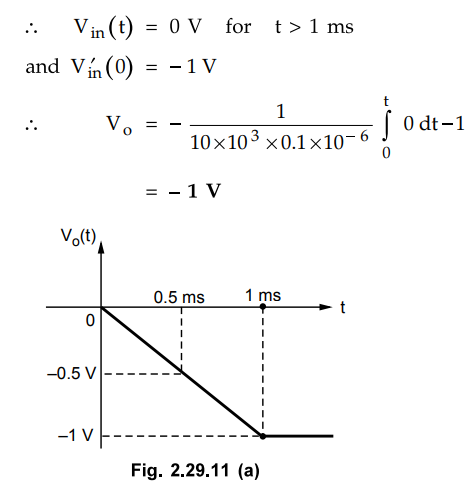
So after t = 1 ms, the output is constant at - 1 V hence the output waveform is as shown in the Fig. 2.29.11 (a). 

 

Example 2.29.3 Consider the lossy integrator as shown in Fig. 2.29.12. For the component values R₁ = 10 kΩ, R_f - 100 kΩ, C_f = 1 nF, determine the lower frequency limit of integration and study the response for the inputs : 1) Step input 2) Square input 3) Sine input.

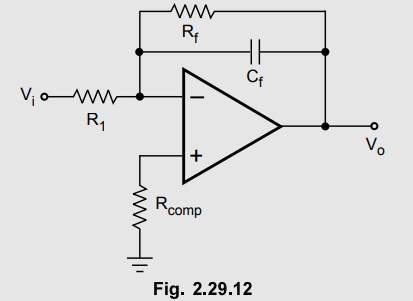
Solution : For the practical integrator,

f_a = 1 / 2πR_fC_f = 1/ 2π × 100 × 10³ × 1 × 10^-9 = 1.5915 kHz

For the responses for step, square and sine inputs, refer section 2.29.2.

Review Questions

1. With the circuit diagram explain the operation of an integrator using op-amp.

Dec.-06,11, May-07,10,12,15, Marks 6

2. Explain why integrators are preferred over differentiators in analog computers.

May-08, Marks 8

3. Explain and draw the output waveforms of the ideal integrator circuit when the input is

i. Sine wave  ii. Step input iii. Square wave.

4. Explain the various errors in an ideal integrator circuit. How these errors are minimized ?

5. Find and R_f  in the loosy integrator so that the peak gain is 40 dB and the gain 3 dB down from its peak occurs at a frequency of 1.25 kHz. Use capacitance of 0.01 µF

[Ans.: 12.70 kQ, 127 Ql

6. An input d.c. voltage as shown in Fig. 2.29.13 is fed to an operational amplifier integrator with RC = 1 second. Find the output and sketch. Opertional amplifier is nulled initially.

May-03, Marks 6

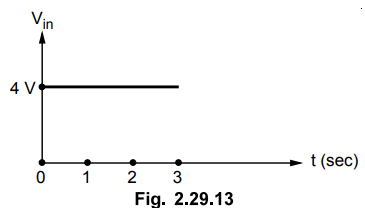
[Ans.: - 4t]